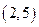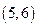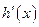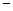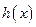(20)(本小題滿分12分)
已知等差數列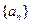 的前3項和為6,前8項和為-4。
的前3項和為6,前8項和為-4。
(Ⅰ)求數列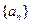 的通項公式;
的通項公式;
(Ⅱ)設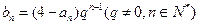 ,求數列
,求數列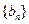 的前n項和
的前n項和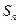
【命題意圖】本小題只要考查數列的基礎知識和化歸、分類整合等數學思想,以及推理論證與分析問題、解決問題的能力.
解:(Ⅰ)設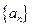 的公差為d.由已知得
的公差為d.由已知得
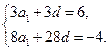
解得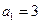 ,
,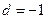 .
.
故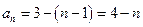 .……………………………………………(5分)
.……………………………………………(5分)
(Ⅱ)由(Ⅰ)得解答可得,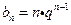 ,于是
,于是
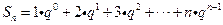 .
.
若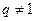 ,將上式兩邊同乘以q有
,將上式兩邊同乘以q有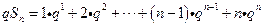 .
.
兩式相減得到
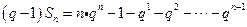
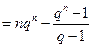
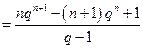 .
.
于是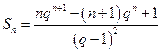 .
.
若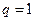 ,則
,則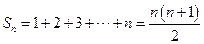 .
.
所以,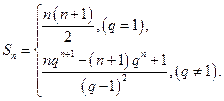 …………………………………(12分)
…………………………………(12分)

(21)(本小題滿分12分)
已知定點A(-1,0),F(2,0),定直線l:x=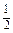 ,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
,不在x軸上的動點P與點F的距離是它到直線l的距離的2倍.設點P的軌跡為E,過點F的直線交E于B、C兩點,直線AB、AC分別交l于點M、N
(Ⅰ)求E的方程;
(Ⅱ)試判斷以線段MN為直徑的圓是否過點F,并說明理由.
【命題意圖】本題主要考查軌跡方程的求解、直線與雙曲線的位置關系,考查解析幾何的思想方法及推理運算能力.
解:(Ⅰ)設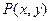 ,則
,則
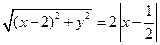 ,
,
化簡得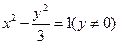 .……………………………………………………(4分)
.……………………………………………………(4分)
(Ⅱ)①當直線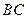 與
與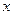 軸不垂直時,設
軸不垂直時,設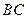 的方程為
的方程為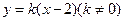 .
.
與雙曲線方程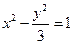 聯立消去
聯立消去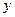 得
得
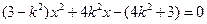 .
.
由題意知,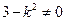 且
且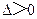 .
.
設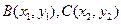 ,則
,則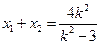 ,
,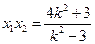 ,
,
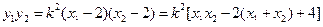
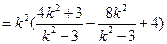
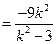 .
.
因為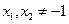 ,
,
所以直線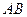 的方程為
的方程為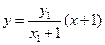 ,因此
,因此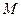 點的坐標為
點的坐標為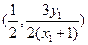 ,
,
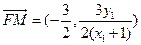 .
.
同理可得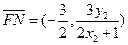 .
.
因此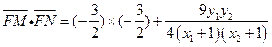
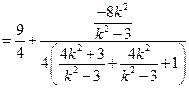
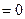 .
.
②當直線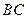 與
與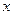 軸垂直時,其方程
軸垂直時,其方程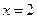 ,則
,則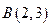 ,
,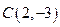 .
.
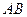 的方程為
的方程為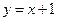 ,因此
,因此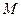 點的坐標
點的坐標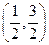 ,
,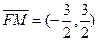 .
.
同理可得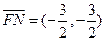 .
.
因此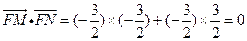 .
.
綜上,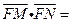
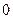 ,即
,即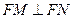 .
.

(22)(本小題滿分14分)
設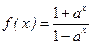 (
(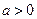 且
且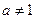 ),g(x)是f(x)的反函數.
),g(x)是f(x)的反函數.
(Ⅰ)求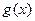 ;
;
(Ⅱ)當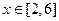 時,恒有
時,恒有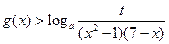 成立,求t的取值范圍;
成立,求t的取值范圍;
(Ⅲ)當0<a≤時,試比較f(1)+f(2)+…+f(n)與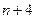 的大小,并說明理由.
的大小,并說明理由.
【命題意圖】本題主要考查函數、反函數、不等式、導數及其應用等基礎知識,考查化歸、分類整合等數學思想,以及推理論證與分析問題、解決問題的能力.
解:(Ⅰ)由題意得,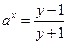 ,
,
故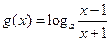 ,
,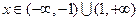 .…………………………………………(3分)
.…………………………………………(3分)
(Ⅱ)由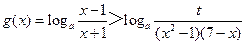 得
得
①當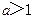 時,
時,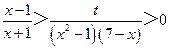 .
.
又因為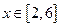 ,所以
,所以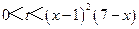 .
.
令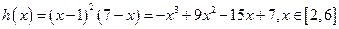 ,
,
則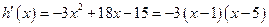 .
.
列表如下:
x | 2 |
| 5 |
| 6 |
| + | 0 |
| ||
| 5 | ↗ | 極大值32 | ↘ | 25 |
所以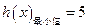 ,
,
所以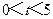 .
.
②當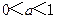 時,
時,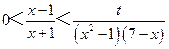 ,
,
又因為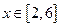 ,所以
,所以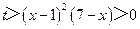 .
.
令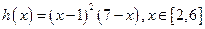 ,
,
由①知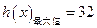 ,
,
所以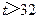 .
.
綜上,當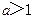 時,
時,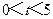 ;當
;當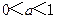 時,
時,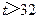 .………………………………(9分)
.………………………………(9分)
(Ⅲ)設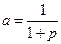 ,則
,則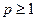 .
.
當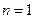 時,
時,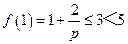 .
.
當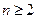 時,
時,
設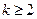 ,
,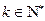 時,
時,
則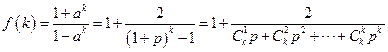 .
.
所以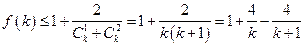 .
.
從而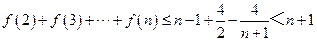 .
.
所以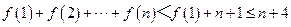 .
.
綜上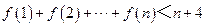 .…………………………(14分)
.…………………………(14分)
【點評】最后一題總體上來說是一道難題,但難中也有簡單部分,因此一定要盡力去做,第(Ⅰ)問是簡單題,第(Ⅱ)問有點難度,雖然涉及到了討論,但考查的內容是我們熟悉的恒成立問題,需要分離參數然后轉化成求最值來解決,所以也不陌生;第(Ⅲ)是難題,用到了放縮法,然后裂項相消求和,不易想到,這一問基本是為極少人準備的.