第Ⅰ卷 (選擇題 共50分)
一、選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一個是符合題目要求的.
1.設(shè)集合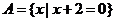 ,集合
,集合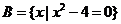 ,則
,則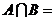 ( )
( )
(A)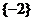 (B)
(B)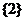 (C)
(C)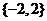 (D)
(D)
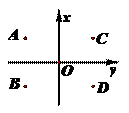
2.如圖,在復(fù)平面內(nèi),點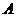 表示復(fù)數(shù)
表示復(fù)數(shù)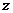 ,則圖中表示
,則圖中表示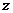 的共軛復(fù)數(shù)的點是( )
的共軛復(fù)數(shù)的點是( )
(A)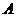 (B)
(B)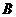 (C)
(C)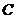 (D)
(D)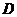
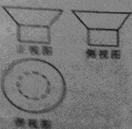
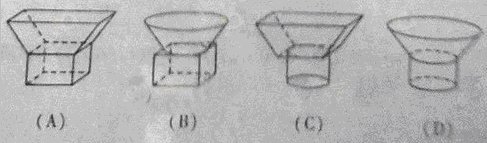
3.一個幾何體的三視圖如圖所示,則該幾何體的直觀圖可以是( )
4.設(shè)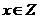 ,集合
,集合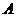 是奇數(shù)集,集合
是奇數(shù)集,集合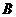 是偶數(shù)集.若命題
是偶數(shù)集.若命題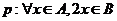 ,則( )
,則( )
(A)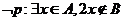 (B)
(B)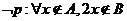
(C)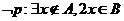 (D)
(D)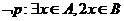
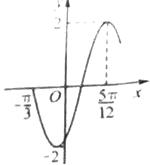
5.函數(shù)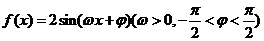 的部分圖象如圖所示,則
的部分圖象如圖所示,則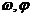 的值分別是( )
的值分別是( )
(A)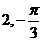 (B)
(B)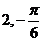 (C)
(C)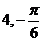 (D)
(D)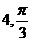
6.拋物線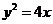 的焦點到雙曲線
的焦點到雙曲線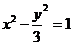 的漸近線的距離是( )
的漸近線的距離是( )
(A)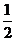 (B)
(B)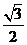 (C)
(C)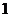 (D)
(D)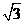
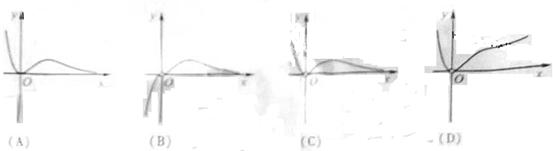
7.函數(shù)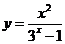 的圖象大致是( )
的圖象大致是( )
8.從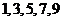 這五個數(shù)中,每次取出兩個不同的數(shù)分別為
這五個數(shù)中,每次取出兩個不同的數(shù)分別為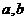 ,共可得到
,共可得到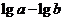 的不同值的個數(shù)是( )
的不同值的個數(shù)是( )
(A)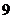 (B)
(B)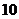 (C)
(C)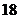 (D)
(D)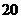
9.節(jié)日 家前的樹上掛了兩串彩燈,這兩串彩燈的第一次閃亮相互獨立,若接通電后的4秒內(nèi)任一時刻等可能發(fā)生,然后每串彩燈在內(nèi)4秒為間隔閃亮,那么這兩串彩燈同時通電后,它們第一次閃亮的時刻相差不超過2秒的概率是( )
(A)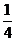 (B)
(B)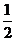 (C)
(C)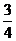 (D)
(D)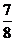
10.設(shè)函數(shù)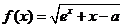 (
(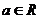 ,
,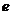 為自然對數(shù)的底數(shù)).若曲線
為自然對數(shù)的底數(shù)).若曲線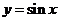 上存在
上存在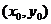 使得
使得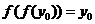 ,則
,則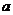 的取值范圍是( )
的取值范圍是( )
(A)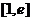 (B)
(B)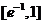 (C)
(C)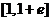 (D)
(D)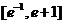
第二部分 (非選擇題 共100分)
二、填空題:本大題共5小題,每小題5分,共25分.
11.二項式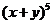 的展開式中,含
的展開式中,含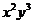 的項的系數(shù)是____________.(用數(shù)字作答)
的項的系數(shù)是____________.(用數(shù)字作答)
12.在平行四邊形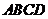 中,對角線
中,對角線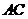 與
與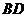 交于點
交于點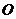 ,
,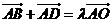 ,則
,則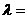 ____________.
____________.
13.設(shè)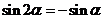 ,
,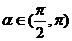 ,則
,則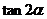 的值是____________.
的值是____________.
14.已知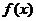 是定義域為
是定義域為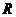 的偶函數(shù),當
的偶函數(shù),當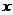 ≥
≥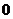 時,
時,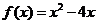 ,那么,不等式
,那么,不等式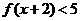 的解集是____________.
的解集是____________.
15.設(shè)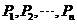 為平面
為平面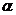 內(nèi)的
內(nèi)的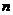 個點,在平面
個點,在平面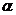 內(nèi)的所有點中,若點
內(nèi)的所有點中,若點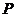 到
到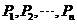 點的距離之和最小,則稱點
點的距離之和最小,則稱點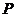 為
為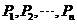 點的一個“中位點”.例如,線段
點的一個“中位點”.例如,線段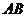 上的任意點都是端點
上的任意點都是端點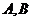 的中位點.則有下列命題:
的中位點.則有下列命題:
①若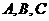 三個點共線,
三個點共線,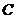 在線段上,則
在線段上,則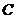 是
是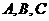 的中位點;
的中位點;
②直角三角形斜邊的點是該直角三角形三個頂點的中位點;
③若四個點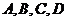 共線,則它們的中位點存在且唯一;
共線,則它們的中位點存在且唯一;
④梯形對角線的交點是該梯形四個頂點的唯一中位點.
其中的真命題是____________.(寫出所有真命題的序號)
三、解答題:本大題共6小題,共75分.解答應(yīng)寫出文字說明,證明過程或演算步驟.
16.(本小題滿分12分) 在等差數(shù)列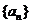 中,
中,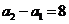 ,且
,且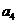 為
為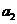 和
和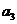 的等比中項,求數(shù)列
的等比中項,求數(shù)列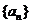 的首項、公差及前
的首項、公差及前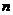 項和.
項和.
17.(本小題滿分12分) 在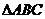 中,角
中,角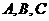 的對邊分別為
的對邊分別為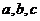 ,且
,且 .
.
(Ⅰ)求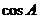 的值;
的值;
(Ⅱ)若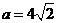 ,
,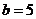 ,求向量
,求向量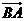 在
在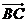 方向上的投影.
方向上的投影.
18.(本小題滿分12分) 某算法的程序框圖如圖所示,其中輸入的變量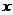 在
在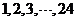 這
這 個整數(shù)中等可能隨機產(chǎn)生.
個整數(shù)中等可能隨機產(chǎn)生.
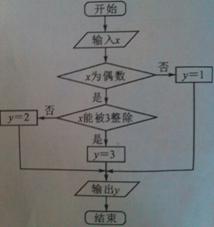
(Ⅰ)分別求出按程序框圖正確編程運行時輸出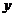 的值為
的值為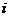 的概率
的概率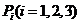 ;
;
(Ⅱ)甲、乙兩同學(xué)依據(jù)自己對程序框圖的理解,各自編寫程序重復(fù)運行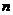 次后,統(tǒng)計記錄了輸出
次后,統(tǒng)計記錄了輸出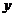 的值為
的值為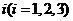 的頻數(shù).以下是甲、乙所作頻數(shù)統(tǒng)計表的部分數(shù)據(jù).
的頻數(shù).以下是甲、乙所作頻數(shù)統(tǒng)計表的部分數(shù)據(jù).
運行 次數(shù) | 輸出 為 | 輸出 為 | 輸出 為 |
|
|
|
|
… | … | … | … |
|
|
|
|
甲的頻數(shù)統(tǒng)計表(部分) 乙的頻數(shù)統(tǒng)計表(部分)
運行 次數(shù) | 輸出 為 | 輸出 為 | 輸出 為 |
|
|
|
|
… | … | … | … |
|
|
|
|
當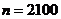 時,根據(jù)表中的數(shù)據(jù),分別寫出甲、乙所編程序各自輸出
時,根據(jù)表中的數(shù)據(jù),分別寫出甲、乙所編程序各自輸出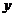 的值為
的值為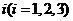 的頻率(用分數(shù)表示),并判斷兩位同學(xué)中哪一位所編寫程序符合算法要求的可能性較大;
的頻率(用分數(shù)表示),并判斷兩位同學(xué)中哪一位所編寫程序符合算法要求的可能性較大;
(Ⅲ)按程序框圖正確編寫的程序運行3次,求輸出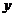 的值為2的次數(shù)
的值為2的次數(shù)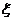 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
19.(本小題滿分12分) 如圖,在三棱柱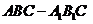 中,側(cè)棱
中,側(cè)棱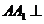 底面
底面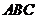 ,
,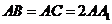 ,
,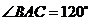 ,
,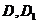 分別是線段
分別是線段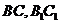 的中點,
的中點,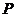 是線段
是線段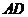 的中點.
的中點.
(Ⅰ)在平面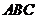 內(nèi),試作出過點
內(nèi),試作出過點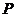 與平面
與平面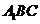 平行的直線
平行的直線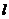 ,說明理由,并證明直線
,說明理由,并證明直線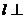 平面
平面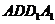 ;
;

(Ⅱ)設(shè)(Ⅰ)中的直線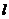 交
交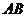 于點
于點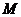 ,交
,交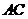 于點
于點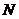 ,求二面角
,求二面角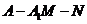 的余弦值.
的余弦值.
20.(本小題滿分13分) 已知橢圓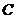 :
: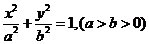 的兩個焦點分別為
的兩個焦點分別為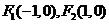 ,且橢圓
,且橢圓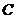 經(jīng)過點
經(jīng)過點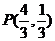 .
.
(Ⅰ)求橢圓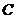 的離心率;
的離心率;
(Ⅱ)設(shè)過點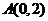 的直線
的直線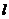 與橢圓
與橢圓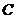 交于
交于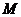 、
、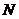 兩點,點
兩點,點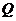 是線段
是線段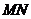 上的點,且
上的點,且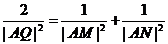 ,求點
,求點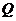 的軌跡方程.
的軌跡方程.
21.(本小題滿分14分)已知函數(shù)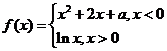 ,其中
,其中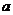 是實數(shù).設(shè)
是實數(shù).設(shè)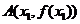 ,
,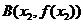 為該函數(shù)圖象上的兩點,且
為該函數(shù)圖象上的兩點,且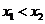 .
.
(Ⅰ)指出函數(shù)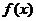 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)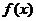 的圖象在點
的圖象在點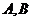 處的切線互相垂直,且
處的切線互相垂直,且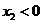 ,求
,求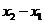 的最小值;
的最小值;
(Ⅲ)若函數(shù)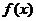 的圖象在點
的圖象在點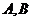 處的切線重合,求
處的切線重合,求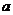 的取值范圍.
的取值范圍.


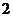 的頻數(shù)
的頻數(shù)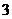 的頻數(shù)
的頻數(shù)