第一部分(選擇題 共60分)
一、選擇題:本大題共12個小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目的要求的.
1.若全集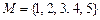 ,
,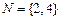 ,則
,則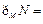
(A)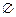 (B)
(B)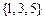 (C)
(C)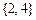 (D)
(D)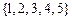
答案:B
解析:∵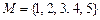 ,則
,則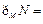
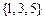 ,選B.
,選B.
2.有一個容量為66的樣本,數(shù)據(jù)的分組及各組的頻數(shù)如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9 [23.5,27.5) 18
[27.5,31.5) 1l [31.5,35.5) 12 [35.5,39.5) 7 [39.5,43.5) 3
根據(jù)樣本的頻率分布估計,大于或等于31.5的數(shù)據(jù)約占
(A)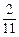 (B)
(B) 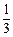 (C)
(C)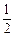 (D)
(D)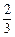
答案:B
解析:大于或等于31.5的數(shù)據(jù)共有12+7+3=22個,約占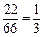 ,選B.
,選B.
3.圓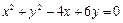 的圓心坐標是
的圓心坐標是
(A)(2,3) (B)(-2,3) (C)(-2,-3) (D)(2,-3)
答案:D
解析:圓方程化為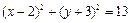 ,圓心(2,-3),選D.
,圓心(2,-3),選D.
4.函數(shù)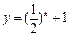 的圖象關于直線y=x對稱的圖象像大致是
的圖象關于直線y=x對稱的圖象像大致是
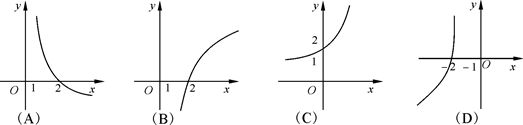
答案:A
解析: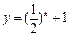 圖象過點
圖象過點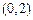 ,且單調(diào)遞減,故它關于直線y=x對稱的圖象過點
,且單調(diào)遞減,故它關于直線y=x對稱的圖象過點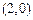 且單調(diào)遞減,選A.
且單調(diào)遞減,選A.
5.“x=3”是“x2=9”的
(A)充分而不必要的條件 (B)必要而不充分的條件
(C)充要條件 (D)既不充分也不必要的條件
答案:A
解析:若x=3,則x 2=9,反之,若x 2=9,則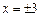 ,選A.
,選A.
6.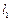 ,
,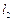 ,
,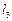 是空間三條不同的直線,則下列命題正確的是
是空間三條不同的直線,則下列命題正確的是
(A)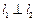 ,
,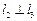
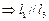 (B)
(B)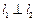 ,
,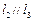
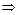
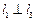
(C)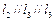
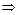
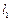 ,
,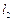 ,
,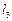 共面 (D)
共面 (D)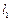 ,
,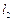 ,
,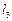 共點
共點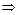
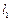 ,
,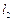 ,
,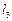 共面
共面
答案:B
解析:由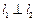 ,
,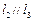 ,根據(jù)異面直線所成角知
,根據(jù)異面直線所成角知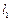 與
與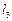 所成角為90°,選B.
所成角為90°,選B.
7.如圖,正六邊形ABCDEF中,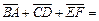
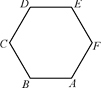
(A)0 (B)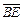
(C)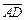 (D)
(D)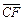
答案:D
解析: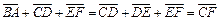 ,選D.
,選D.
8.在△ABC中,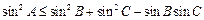 ,則A的取值范圍是
,則A的取值范圍是
(A)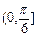 (B)
(B)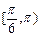 (C)
(C)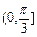 (D)
(D)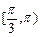
答案:C
解析:由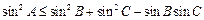 得
得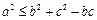 ,即
,即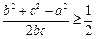 ,
,
∴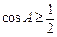 ,∵
,∵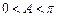 ,故
,故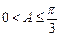 ,選C.
,選C.
9.數(shù)列{an}的前n項和為Sn,若a1=1,an+1 =3Sn(n ≥1),則a6=
(A)3 × 44 (B)3 × 44+1 (C)44 (D)44+1
答案:A
解析:由an+1 =3Sn,得an =3Sn-1(n ≥ 2),相減得an+1-an =3(Sn-Sn-1)= 3an,則an+1=4an(n ≥ 2),a1=1,a2=3,則a6= a2·44=3×44,選A.
10.某運輸公司有12名駕駛員和19名工人,有8輛載重量為10噸的甲型卡車和7輛載重量為6噸的乙型卡車.某天需運往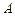 地至
地至 少72噸的貨
少72噸的貨 物,派用的每輛車需滿載且只運送一次.派用的每輛甲型卡車需配2名工人,運送一次可得利潤450元;派用的每輛乙型卡車需配1名工人,運送一次可得利潤350元,該公司合理計劃當天派用兩類卡車的車輛數(shù),可得最大利潤為
物,派用的每輛車需滿載且只運送一次.派用的每輛甲型卡車需配2名工人,運送一次可得利潤450元;派用的每輛乙型卡車需配1名工人,運送一次可得利潤350元,該公司合理計劃當天派用兩類卡車的車輛數(shù),可得最大利潤為
(A)4650元 (B)4700元 (C)4900元 (D)5000元
答案:C
解析:設派用甲型卡車x(輛),乙型卡車y(輛),獲得的利潤為u(元),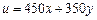 ,由題意,x、y滿足關系式
,由題意,x、y滿足關系式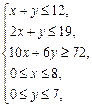 作出相應的平面區(qū)域,
作出相應的平面區(qū)域,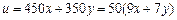 在由
在由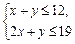 確定的交點
確定的交點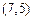 處取得最大值4900元,選C.
處取得最大值4900元,選C.
11.在拋物線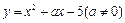 上取橫坐標為
上取橫坐標為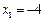 ,
,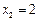 的兩點,過這兩點引一條割線,有平行于該割線的一條直線同時與拋物線和圓
的兩點,過這兩點引一條割線,有平行于該割線的一條直線同時與拋物線和圓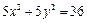 相切,則拋物線頂點的坐標為
相切,則拋物線頂點的坐標為
(A)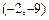 (B)
(B)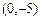 (C)
(C)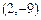 (D)
(D)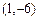
答案:A
解析:令拋物線上橫坐標為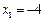 、
、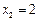 的點為
的點為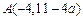 、
、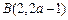 ,則
,則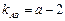 ,由
,由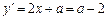 ,故切點為
,故切點為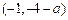 ,切線方程為
,切線方程為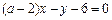 ,該直線又和圓相切,則
,該直線又和圓相切,則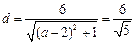 ,解得
,解得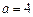 或
或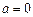 (舍去),則拋物線為
(舍去),則拋物線為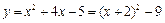 ,定點坐標為
,定點坐標為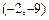 ,選A.
,選A.
12.在集合 中任取一個偶數(shù)a和一個奇數(shù)b構成以原點為起點的向量
中任取一個偶數(shù)a和一個奇數(shù)b構成以原點為起點的向量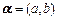 ,從所有得到的以原點為起點的向量中任取兩個向量為鄰邊作平行四邊形,記所有作成的平行四邊形的個數(shù)為n,其中面積等于2的平行四邊形的個數(shù)為
,從所有得到的以原點為起點的向量中任取兩個向量為鄰邊作平行四邊形,記所有作成的平行四邊形的個數(shù)為n,其中面積等于2的平行四邊形的個數(shù)為 m,則
m,則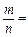
(A)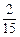 (B)
(B)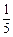 (
( C)
C)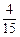 (D)
(D)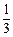
答案:B
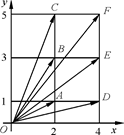
解析:∵以原點為起點的向量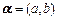 有
有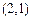 、
、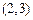 、
、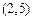 、
、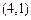 、
、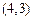 、
、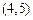 共6個,可作平行四邊形的個數(shù)
共6個,可作平行四邊形的個數(shù)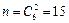 個,結合圖形進行計算,其中由
個,結合圖形進行計算,其中由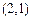
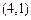 、
、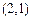
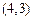 、
、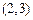
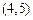 確定的平行四邊形面積為2,共有3個,則
確定的平行四邊形面積為2,共有3個,則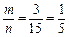 ,選B.
,選B.
第二部分(非選擇題 共90分)
二、填空題:本大題共4小題,每小題4分,共16分.
13.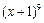 的展開式中
的展開式中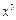 的系數(shù)是_________.(用數(shù)字作答)
的系數(shù)是_________.(用數(shù)字作答)
答案:84
解析:∵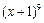 的展開式中
的展開式中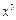 的系數(shù)是
的系數(shù)是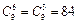 .
.
14.雙曲線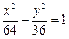 上一點P到雙曲線右焦點的距離是4,那么P到左準線的距離是____.
上一點P到雙曲線右焦點的距離是4,那么P到左準線的距離是____.
答案:16
答案:16
解析:離心率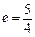 ,設P到右準線的距離是d,則
,設P到右準線的距離是d,則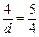 ,則
,則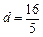 ,則P到左準線的距離等于
,則P到左準線的距離等于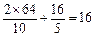 .
.
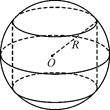
15.如圖,半徑為4的球O中有一內(nèi)接圓柱.當圓柱的側(cè)面積最大時,球的表面積與該圓柱的側(cè)面積之差是_________.
答案:32π
解析:如圖,設球一條半徑與圓柱相應的母線夾角為α,圓柱側(cè)面積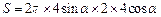 =
=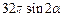 ,當
,當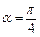 時,S取最大值
時,S取最大值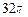 ,此時球的表面積與該圓柱的側(cè)面積之差為
,此時球的表面積與該圓柱的側(cè)面積之差為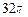 .
.
16.函數(shù)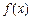 的定義域為A,若
的定義域為A,若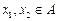 且
且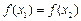 時總有
時總有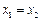 ,則稱
,則稱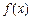 為單函數(shù).例如,函數(shù)
為單函數(shù).例如,函數(shù)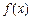 =2x+1(
=2x+1(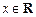 )是單函數(shù).下列命題:
)是單函數(shù).下列命題:
①函數(shù)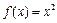 (x
(x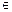 R)是單函數(shù);
R)是單函數(shù);
②指數(shù)函數(shù)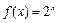 (x
(x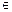 R)是單函數(shù);
R)是單函數(shù);
③若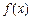 為單函數(shù),
為單函數(shù),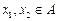 且
且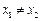 ,則
,則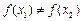 ;
;
④在定義域上具有單調(diào)性的函數(shù)一定是單函數(shù).
其中的真命題是_________.(寫出所有真命題的編號)
答案:②③④
解析:對于①,若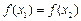 ,則
,則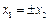 ,不滿足;②是單函數(shù);命題③實際上是單函數(shù)命題的逆否命題,故為真命題;根據(jù)定義,命題④滿足條件.
,不滿足;②是單函數(shù);命題③實際上是單函數(shù)命題的逆否命題,故為真命題;根據(jù)定義,命題④滿足條件.











