第一部分 (選擇題 共60分)
一、選擇題:每小題給出的四個選項中,只有一項是符合題目要求的。
1、設集合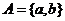 ,
,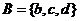 ,則
,則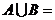 ( )
( )
A、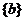 B、
B、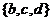 C、
C、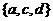 D、
D、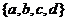
[答案]D
[解析]集合A中包含a,b兩個元素,集合B中包含b,c,d三個元素,共有a,b,c,d四個元素,所以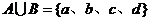
[點評]本題旨在考查集合的并集運算,集合問題屬于高中數學入門知識,考試時出題難度不大,重點是掌握好課本的基礎知識.
2、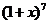 的展開式中
的展開式中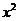 的系數是( )
的系數是( )
A、21 B、28 C、35 D、42
[答案]A
[解析]二項式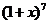 展開式的通項公式為
展開式的通項公式為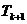 =
=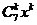 ,令k=2,則
,令k=2,則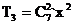
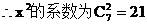
[點評]高考二項展開式問題題型難度不大,要得到這部分分值,首先需要熟練掌握二項展開式的通項公式,其次需要強化考生的計算能力.
3、交通管理部門為了解機動車駕駛員(簡稱駕駛員)對某新法規的知曉情況,對甲、乙、丙、丁四個社區做分層抽樣調查。假設四個社區駕駛員的總人數為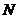 ,其中甲社區有駕駛員96人。若在甲、乙、丙、丁四個社區抽取駕駛員的人數分別為12,21,25,43,則這四個社區駕駛員的總人數
,其中甲社區有駕駛員96人。若在甲、乙、丙、丁四個社區抽取駕駛員的人數分別為12,21,25,43,則這四個社區駕駛員的總人數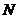 為( )
為( )
A、101 B、808 C、1212 D、2012
[答案]B
[解析]N=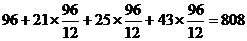
[點評]解決分層抽樣問題,關鍵是求出抽樣比,此類問題難點要注意是否需要剔除個體.
4、函數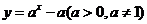 的圖象可能是( )
的圖象可能是( )
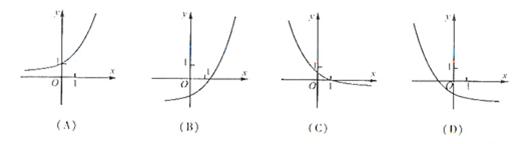
[答案]C
[解析]采用特殊值驗證法. 函數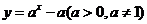 恒過(1,0),只有C選項符合.
恒過(1,0),只有C選項符合.
[點評]函數大致圖像問題,解決方法多樣,其中特殊值驗證、排除法比較常用,且簡單易用.
5、如圖,正方形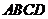 的邊長為
的邊長為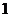 ,延長
,延長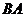 至
至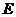 ,使
,使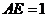 ,連接
,連接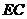 、
、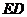 則
則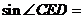 ( )
( )
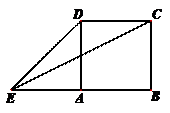
A、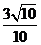 B、
B、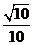 C、
C、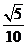 D、
D、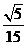
[答案]B
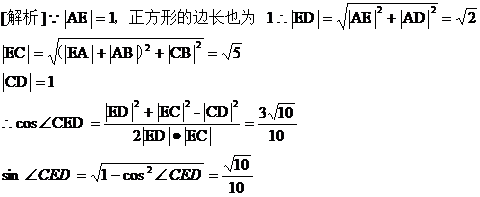
[點評]注意恒等式sin2α+cos2α=1的使用,需要用α的的范圍決定其正余弦值的正負情況.
6、下列命題正確的是( )
A、若兩條直線和同一個平面所成的角相等,則這兩條直線平行
B、若一個平面內有三個點到另一個平面的距離相等,則這兩個平面平行
C、若一條直線平行于兩個相交平面,則這條直線與這兩個平面的交線平行
D、若兩個平面都垂直于第三個平面,則這兩個平面平行
[答案]C
[解析]若兩條直線和同一平面所成角相等,這兩條直線可能平行,也可能為異面直線,也可能相交,所以A錯;一個平面不在同一條直線的三點到另一個平面的距離相等,則這兩個平面平行,故B錯;若兩個平面垂直同一個平面兩平面可以平行,也可以垂直;故D錯;故選項C正確.
[點評]本題旨在考查立體幾何的線、面位置關系及線面的判定和性質,需要熟練掌握課本基礎知識的定義、定理及公式.
7、設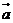 、
、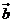 都是非零向量,下列四個條件中,使
都是非零向量,下列四個條件中,使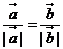 成立的充分條件是( )
成立的充分條件是( )
A、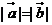 且
且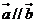 B、
B、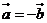 C、
C、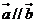 D、
D、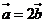
[答案]D
[解析]若使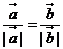 成立,則
成立,則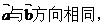 選項中只有D能保證,故選D.
選項中只有D能保證,故選D.
[點評]本題考查的是向量相等條件 模相等且方向相同.學習向量知識時需注意易考易錯零向量,其模為0且方向任意.
模相等且方向相同.學習向量知識時需注意易考易錯零向量,其模為0且方向任意.
8、若變量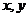 滿足約束條件
滿足約束條件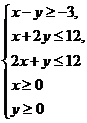 ,則
,則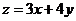 的最大值是( )
的最大值是( )
A、12 B、26 C、28 D、33
[答案]C
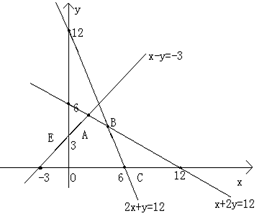
[解析]目標函數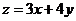 可以變形為
可以變形為
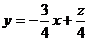 ,做函數
,做函數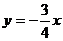 的平行線,
的平行線,
當其經過點B(4,4)時截距最大時,
即z有最大值為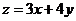 =
=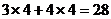 .
.
[點評]解決線性規劃題目的常規步驟:
一列(列出約束條件)、
二畫(畫出可行域)、
三作(作目標函數變形式的平行線)、
四求(求出最優解).
9、已知拋物線關于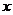 軸對稱,它的頂點在坐標原點
軸對稱,它的頂點在坐標原點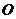 ,
,
并且經過點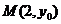 。若點
。若點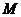 到該拋物線焦點的距離為
到該拋物線焦點的距離為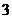 ,則
,則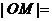 ( )
( )
A、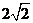 B、
B、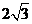 C、
C、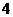 D、
D、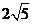
[答案]B
[解析]設拋物線方程為y2=2px(p>0),則焦點坐標為(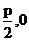 ),準線方程為x=
),準線方程為x=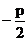 ,
,
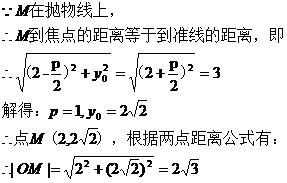
[點評]本題旨在考查拋物線的定義: |MF|=d,(M為拋物線上任意一點,F為拋物線的焦點,d為點M到準線的距離).
10、如圖,半徑為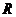 的半球
的半球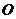 的底面圓
的底面圓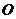 在平面
在平面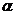 內,過點
內,過點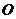 作平面
作平面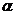 的垂線交半球面于點
的垂線交半球面于點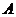 ,過圓
,過圓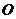 的直徑
的直徑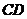 作平面
作平面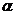 成
成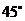 角的平面與半球面相交,所得交線上到平面
角的平面與半球面相交,所得交線上到平面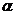 的距離最大的點為
的距離最大的點為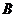 ,該交線上的一點
,該交線上的一點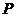 滿足
滿足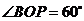 ,則
,則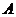 、
、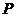 兩點間的球面距離為( )
兩點間的球面距離為( )
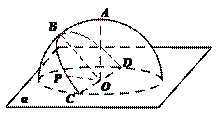
A、 B、
B、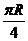 C、
C、 D、
D、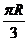
[答案]A
[解析]以O為原點,分別以OB、OC、OA所在直線為x、y、z軸,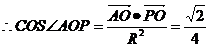 則
則
A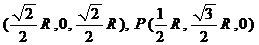
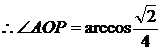
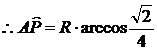
[點評]本題綜合性較強,考查知識點較為全面,題設很自然的把向量、立體幾何、三角函數等基礎知識結合到了一起.是一道知識點考查較為全面的好題.要做好本題需要有扎實的數學基本功.
11、方程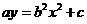 中的
中的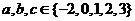 ,且
,且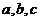 互不相同,在所有這些方程所表示的曲線中,不同的拋物線共有( )
互不相同,在所有這些方程所表示的曲線中,不同的拋物線共有( )
A、28條 B、32條 C、36條 D、48條
[答案]B
[解析]方程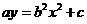 變形得
變形得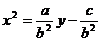 ,若表示拋物線,則
,若表示拋物線,則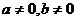
所以,分b=-2,1,2,3四種情況:
(1)若b=-2,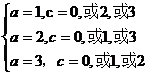 ; (2)若b=2,
; (2)若b=2, 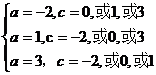
以上兩種情況下有4條重復,故共有9+5=14條;
同理 若b=1,共有9條; 若b=3時,共有9條.
綜上,共有14+9+9=32種
[點評]此題難度很大,若采用排列組合公式計算,很容易忽視重復的4條拋物線. 列舉法是解決排列、組合、概率等非常有效的辦法.要能熟練運用.
12、設函數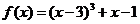 ,
,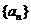 是公差不為0的等差數列,
是公差不為0的等差數列,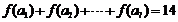 ,則
,則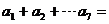 ( )
( )
A、0 B、7 C、14 D、21
[答案]D
[解析]∵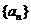 是公差不為0的等差數列,且
是公差不為0的等差數列,且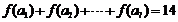
∴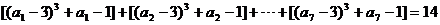
∴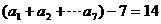
∴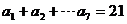
[點評]本小題考查的知識點較為綜合,既考查了高次函數的性質又考查了等差數列性質的應用,解決此類問題必須要敢于嘗試,并需要認真觀察其特點.











