第二部分 (非選擇題 共90分)
二、填空題(本大題共4個小題,每小題4分,共16分。把答案填在答題紙的相應位置上。)
13、函數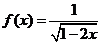 的定義域是____________。(用區間表示)
的定義域是____________。(用區間表示)
[答案](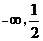 )
)
[解析]由分母部分的1-2x>0,得到x∈(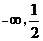 ).
).
[點評]定義域問題屬于低檔題,只要保證式子有意義即可,相對容易得分.常見考點有:分母不為0;偶次根下的式子大于等于0;對數函數的真數大于0;0的0次方沒有意義.
 14、如圖,在正方體
14、如圖,在正方體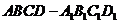 中,
中,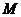 、
、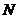 分別是
分別是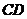 、
、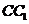 的中點,則異面直線
的中點,則異面直線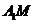 與
與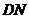 所成的角的大小是____________。
所成的角的大小是____________。
[答案]90º
[解析]方法一:連接D1M,易得DN⊥A1D1 ,DN⊥D1M,
所以,DN⊥平面A1MD1,
又A1M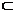 平面A1MD1,所以,DN⊥A1D1,故夾角為90º
平面A1MD1,所以,DN⊥A1D1,故夾角為90º
方法二:以D為原點,分別以DA, DC, DD1為x, y, z軸,建立空間直角坐標系D—xyz.設正方體邊長為2,則D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2)
故,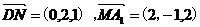
所以,cos<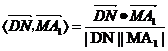 = 0,故DN⊥D1M,所以夾角為90º
= 0,故DN⊥D1M,所以夾角為90º
[點評]異面直線夾角問題通常可以采用兩種途徑: 第一,把兩條異面直線平移到同一平面中借助三角形處理; 第二,建立空間直角坐標系,利用向量夾角公式解決.
15、橢圓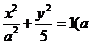 為定值,且
為定值,且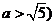 的的左焦點為
的的左焦點為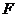 ,直線
,直線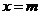 與橢圓相交于點
與橢圓相交于點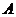 、
、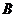 ,
,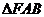 的周長的最大值是12,則該橢圓的離心率是______。
的周長的最大值是12,則該橢圓的離心率是______。
[答案] 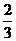
[解析]根據橢圓定義知:4a=12, 得a=3 , 又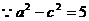
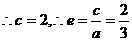
[點評]本題考查對橢圓概念的掌握程度.突出展現高考前的復習要回歸課本的新課標理念.
16、設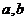 為正實數,現有下列命題:
為正實數,現有下列命題:
①若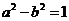 ,則
,則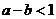 ;
;
②若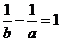 ,則
,則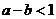 ;
;
③若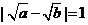 ,則
,則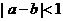 ;
;
④若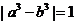 ,則
,則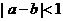 。
。
其中的真命題有____________。(寫出所有真命題的編號)
[答案] ①④
[解析]若a,b都小于1,則a-b<1
若a,b中至少有一個大于等于1, 則a+b>1,
由a2-b2=(a+b)(a-b)=1 ,所以,a-b<1 故①正確.
對于|a3-b3|=|(a-b)(a2+ab+b2)|=1,
若a,b中至少又一個大于等于1,則a2+ab+b2>1,則|a-b|<1
若a,b都小于1,則|a-b|<1,所以④正確.
綜上,真命題有 ① ④ .
[點評]此類問題考查難度較大,要求對四個備選項都要有正確的認識,需要考生具備扎實的數學基礎,平時應多加強這類題的限時性練習.











