三、解答題(本大題共6個小題,共74分。解答應寫出必要的文字說明,證明過程或演算步驟。)
17、(本小題滿分12分) 某居民小區有兩個相互獨立的安全防范系統(簡稱系統)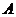 和
和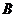 ,系統
,系統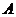 和系統
和系統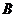 在任意時刻發生故障的概率分別為
在任意時刻發生故障的概率分別為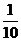 和
和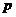 。
。
(Ⅰ)若在任意時刻至少有一個系統不發生故障的概率為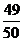 ,求
,求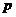 的值;
的值;
(Ⅱ)求系統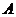 在3次相互獨立的檢測中不發生故障的次數大于發生故障的次數的概率。
在3次相互獨立的檢測中不發生故障的次數大于發生故障的次數的概率。
[解析](1)設:“至少有一個系統不發生故障”為事件C,那么
1-P(C)=1-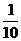 P=
P=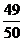 ,解得P=
,解得P=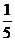 ………………………………6 分
………………………………6 分
(2)設“系統A在3次相互獨立的檢測中不發生故障的次數大于發生故障的次數”為
事件D,
那么P(D)=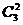

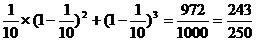
答:檢測中不發生故障的次數大于發生故障的次數的概率為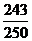 . ………………12分.
. ………………12分.
[點評]本小題主要考查相互獨立事件,獨立重復試驗、互斥事件等概念及相關計算,考查運用概率知識與方法解決實際問題的能力.
18、(本小題滿分12分) 已知函數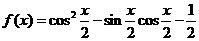 。
。
(Ⅰ)求函數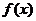 的最小正周期和值域;
的最小正周期和值域;
(Ⅱ)若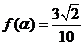 ,求
,求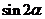 的值。
的值。
[解析](1)由已知,f(x)=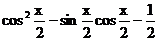
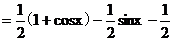
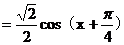
所以f(x)的最小正周期為2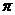 ,值域為
,值域為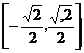 。…………………6分
。…………………6分
(2)由(1)知,f(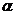 )=
)=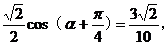
所以cos(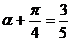 )。
)。
所以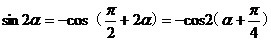
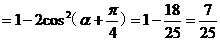 ,…………………12分
,…………………12分
[點評]本小題主要考查三角函數的性質、兩角和的正(余)弦公式、二倍角公式等基礎知識,考查運算能力,考查化歸與轉化等數學思想.
19、(本小題滿分12分) 如圖,在三棱錐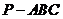 中,
中,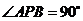 ,
,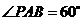 ,
,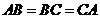 ,點
,點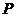 在平面
在平面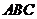 內的射影
內的射影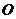 在
在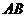 上。
上。
(Ⅰ)求直線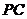 與平面
與平面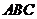 所成的角的大小;
所成的角的大小;
(Ⅱ)求二面角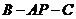 的大小。
的大小。
[解析](1)連接OC. 由已知,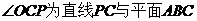 所成的角
所成的角
設AB的中點為D,連接PD、CD.
因為AB=BC=CA,所以CD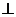 AB.
AB.
因為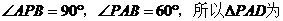 等邊三角形,
等邊三角形,
不妨設PA=2,則OD=1,OP=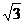 , AB=4.
, AB=4.
所以CD=2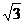 ,OC=
,OC=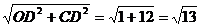 .
.
在Rt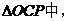 tan
tan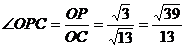 .…………………………6分
.…………………………6分
(2)過D作DE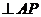 于E,連接CE.
于E,連接CE.
由已知可得,CD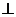 平面PAB.
平面PAB.
據三垂線定理可知,CE⊥PA,
所以,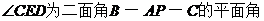 .
.
由(1)知,DE=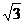
在Rt△CDE中,tan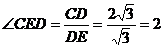
故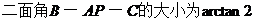 …………………………………12分
…………………………………12分
[點評]本題旨在考查線面位置關系和二面角的基礎概念,重點考查思維能力和空間想象能力,進一步深化對二面角的平面角的求解.求解二面角平面角的常規步驟:一找(尋找現成的二面角的平面角)、二作(若沒有找到現成的,需要引出輔助線作出二面角的平面角)、三求(有了二面角的平面角后,在三角形中求出該角相應的三角函數值).
20、(本小題滿分12分) 已知數列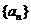 的前
的前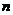 項和為
項和為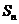 ,常數
,常數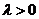 ,且
,且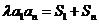 對一切正整數
對一切正整數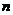 都成立。
都成立。
(Ⅰ)求數列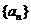 的通項公式;
的通項公式;
(Ⅱ)設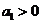 ,
,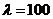 ,當
,當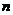 為何值時,數列
為何值時,數列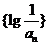 的前
的前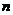 項和最大?
項和最大?
[解析]取n=1,得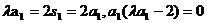
若a1=0,則s1=0, 當n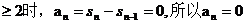
若a1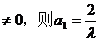 , 當n
, 當n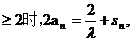
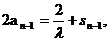
上述兩個式子相減得:an=2an-1,所以數列{an}是等比數列
綜上,若a1 = 0, 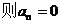
若a1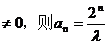 …………………………………………7分
…………………………………………7分
(2)當a1>0,且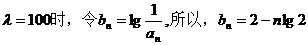
所以,{bn}單調遞減的等差數列(公差為-lg2)
則 b1>b2>b3>…>b6=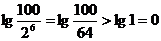
當n≥7時,bn≤b7=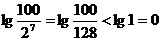
故數列{lg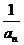 }的前6項的和最大. …………………………12分
}的前6項的和最大. …………………………12分
[點評]本小題主要從三個層面對考生進行了考查. 第一,知識層面:考查等差數列、等比數列、對數等基礎知識;第二,能力層面:考查思維、運算、分析問題和解決問題的能力;第三,數學思想:考查方程、分類與整合、化歸與轉化等數學思想.
21、(本小題滿分12分) 如圖,動點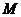 與兩定點
與兩定點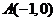 、
、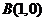 構成
構成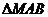 ,且直線
,且直線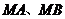 的斜率之積為4,設動點
的斜率之積為4,設動點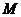 的軌跡為
的軌跡為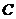 。
。
(Ⅰ)求軌跡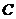 的方程;
的方程;
(Ⅱ)設直線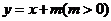 與
與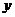 軸交于點
軸交于點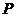 ,與軌跡
,與軌跡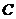 相交于點
相交于點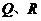 ,且
,且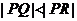 ,求
,求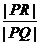 的取值范圍。
的取值范圍。
[解析](1)設M的坐標為(x,y),當x=-1時,直線MA的斜率不存在;當x=1時,直線MB的斜率不存在。
于是x≠1且x≠-1.此時,MA的斜率為
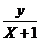 ,MB的斜率為
,MB的斜率為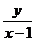 .
.
由題意,有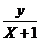 ·
·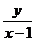 =4
=4
化簡可得,4x2-y2-4=0
故動點M的軌跡C的方程為4x2-y2-4=0(x≠1且x≠-1)…………………………4分
(2)由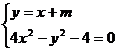 消去y,可得3x2-2mx-m2-4=0. (﹡)
消去y,可得3x2-2mx-m2-4=0. (﹡)
對于方程(﹡),其判別式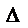 =(-2m)2-4×3(-m2-4)=16m2+48>0
=(-2m)2-4×3(-m2-4)=16m2+48>0
而當1或-1為方程(*)的根時,m的值為-1或1.
結合題設(m>0)可知,m>0,且m≠1
設Q、R的坐標分別為(XQ,YQ),(XR,YR),則為方程(*)的兩根.
因為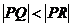 ,所以
,所以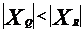 ,
,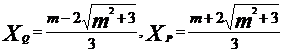
所以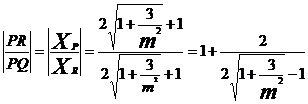 。
。
此時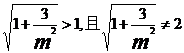
所以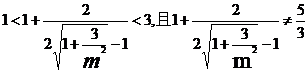
所以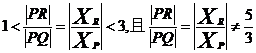
綜上所述, …………………………12分
…………………………12分
[點評]本小題主要考察直線、雙曲線、軌跡方程的求法等基礎知識,考察思維能力、運算能力,考察函數、分類與整合等思想,并考察思維的嚴謹性。
22、(本小題滿分14分) 已知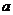 為正實數,
為正實數,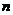 為自然數,拋物線
為自然數,拋物線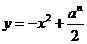 與
與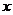 軸正半軸相交于點
軸正半軸相交于點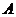 ,設
,設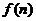 為該拋物線在點
為該拋物線在點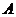 處的切線在
處的切線在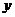 軸上的截距。
軸上的截距。
(Ⅰ)用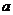 和
和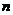 表示
表示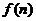 ;
;
(Ⅱ)求對所有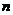 都有
都有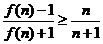 成立的
成立的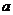 的最小值;
的最小值;
(Ⅲ)當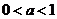 時,比較
時,比較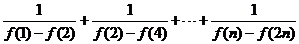 與
與
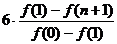 的大小,并說明理由。
的大小,并說明理由。
[解析](1)由已知得,交點A的坐標為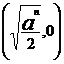 ,對
,對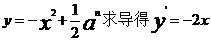
則拋物線在點A處的切線方程為:
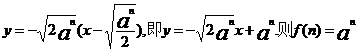 ………………4分
………………4分
(2)由(1)知f(n)=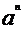 ,則
,則
即知,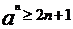 對于所有的n成立,
對于所有的n成立,
特別地,當n=1時,得到a≥3
當a=3,n≥1時,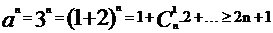
當n=0時,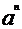 =2n+1.故a=3時
=2n+1.故a=3時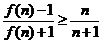 對所有自然數n均成立.
對所有自然數n均成立.
所以滿足條件的a的最小值為3. ………………………………………………8分
(3)由(1)知f(k)=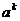
下面證明: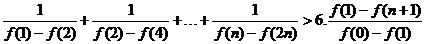
首先證明0<x<1時,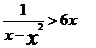
設函數g(x)=6x(x2-x)+1,0<x<1, 則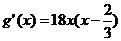 .
.
當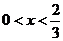 時,g'(x)<0; 當
時,g'(x)<0; 當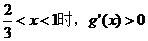
故g(x)在區間(0,1)上的最小值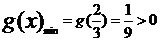
所以,當0<x<1時,g(x)>0,即得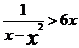
由0<a<1知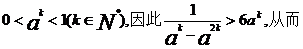
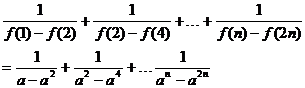
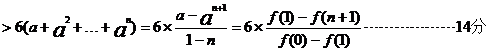
[點評]本小題屬于高檔題,難度較大,需要考生具備扎實的數學基礎和解決數學問題的能力.主要考查了導數的應用、不等式、數列等基礎知識;考查了思維能力、運算能力、分析問題與解決問題的能力和創新意識能力;且又深層次的考查了函數、轉換與化歸、特殊與一般等數學思維方法。











