一、選擇題
(1)設集合A={3,5,6,8},集合B={4,5,7,8},則A n B等于
(A){3,4,5,6,7,8} (B){3,6} (C) {4,7} (D){5,8}
1. 答案D
【命題意圖】本題主要考查集合的交集運算.
【解析】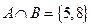 ,故選D.
,故選D.
(2)函數Y=l 2的圖象大致是
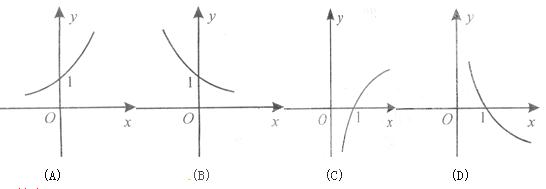
2. 答案C
【命題意圖】本題主要考查對數函數的圖象.
【解析】該對數函數的圖象過(1,0),且單調遞增,故選C.
(3)拋物線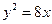 的焦點到準線的距離是
的焦點到準線的距離是
(A)1 (B)2 (C)4 (D)8
3. 答案C
【命題意圖】本題主要考查拋物線的方程及性質.
【解析】焦點到準線的距離是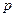 ,
,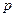 =4,故選C.
=4,故選C.
(4)一個單位有職工800人,期中具有高級職稱的160人,具有中級職稱的320人,具有 初級職稱的200人,其余人員120人.為了解職工收入情況,決定采用
初級職稱的200人,其余人員120人.為了解職工收入情況,決定采用 分層抽樣的方
分層抽樣的方 法,從中抽取容量為40的樣本.則從上述各層中依次抽取的人數分別是
法,從中抽取容量為40的樣本.則從上述各層中依次抽取的人數分別是
(A)12,24,15,9(B)9,12,12,7(C)8,15,12,5(D)8,16,10,6
4.答案D
【命題意圖】本題主要考查分層抽樣知識.
【解析】∵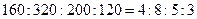 ,∴各層抽取的人數分別是8,16,10,6,故選D.
,∴各層抽取的人數分別是8,16,10,6,故選D.
(5)函數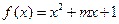 的圖像關于直線
的圖像關于直線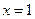 對稱的充要條件是
對稱的充要條件是
(A)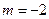 (B)
(B)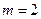 (C)
(C)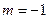 (D)
(D)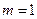
5. 答案A
【命題意圖】本題主要考查二次函數的對稱性和充分必要條件.
【解析】該二次函數的對稱軸是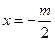 ,∴
,∴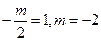 ,故選A.
,故選A.
(6)設點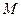 是線段
是線段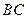 的中點,點
的中點,點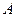 在直線
在直線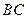 外,
外,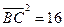 ,
,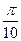
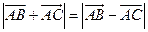 ,則
,則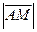
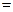
(A)8(B)4 (C)2 (D)1
6. 答案C
【命題意圖】本題主要考查平面向量的基本運算.
【解析】由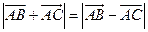 ,兩邊平方得,
,兩邊平方得,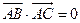 ,∴
,∴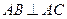 ,△ABC為直角三角形,BC為斜邊,∴
,△ABC為直角三角形,BC為斜邊,∴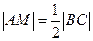 ,由已知得
,由已知得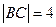 ,∴
,∴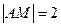 ,故選C.
,故選C.
(7)將函數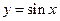 的圖像上所有的點向右平行移動
的圖像上所有的點向右平行移動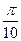 個單位長度,再把所得各點的橫坐標伸長到原來的2倍(縱坐標不變),所得圖像的函數解析式是
個單位長度,再把所得各點的橫坐標伸長到原來的2倍(縱坐標不變),所得圖像的函數解析式是
(A)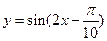
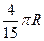 (B)
(B)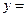
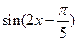
(C)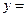
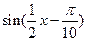 (D)
(D)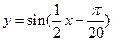
7. 答案C
【命題意圖】本題主要考查三角函數圖象的平移變換和伸縮變換.
【解析】將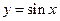 圖象向右平移
圖象向右平移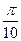 個單位得到函數
個單位得到函數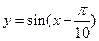 ,再把橫坐標伸長為原來的2倍得到
,再把橫坐標伸長為原來的2倍得到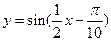 ,故選C.
,故選C.
(8)某加工廠用某原料由甲車間加工出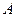 產品,由乙車間加工出
產品,由乙車間加工出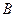 產品.甲車間加工一箱原料需耗費工時10小時可加工出7千克
產品.甲車間加工一箱原料需耗費工時10小時可加工出7千克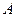 產品,每千克
產品,每千克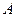 產品獲利40元.乙車間加工一箱原料需耗費工時6小時可加工出4千克
產品獲利40元.乙車間加工一箱原料需耗費工時6小時可加工出4千克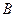 產品,每千克
產品,每千克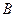 產品獲利50元.甲、乙兩車間每天共能完成至多70箱原料的加工,每天甲、乙車間耗費工時總和不得超過480小時,甲、乙兩車間每天獲利最大的生產計劃為
產品獲利50元.甲、乙兩車間每天共能完成至多70箱原料的加工,每天甲、乙車間耗費工時總和不得超過480小時,甲、乙兩車間每天獲利最大的生產計劃為
(A)甲車間加工原料10箱,乙車間加工原料60箱
(B)甲車間加工原料15箱,乙車間加工原料55箱
(C)甲車間加工原料18箱,乙車間加工原料50箱
(D)甲車間加工原料40箱,乙車間加工原料30箱
8. 答案B
【命題意圖】本題主要考查線性規劃的實際問題.
【解析】設甲車間生產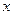 箱,乙車間生產
箱,乙車間生產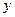 箱,則所獲利潤
箱,則所獲利潤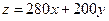 ,由已知條件
,由已知條件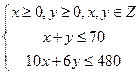 ,可行域為
,可行域為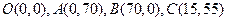 構成的四邊形,∴過點C取得最大值,故選B.
構成的四邊形,∴過點C取得最大值,故選B.
(9)由1、2、3、4、5組成沒有重復數字且1、2都不與5相鄰的五位數的個數是
(A)36(B)3 2(C)28 (D)24
2(C)28 (D)24
9. 答案A 【命題意圖】本題主要考查排列組合知識和分類討論的思想方法.
【解析】①若5在個位或萬位,有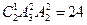 種方法;②若5在中間三位,則有
種方法;②若5在中間三位,則有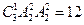 種方法,故有36種方法,故選A.
種方法,故有36種方法,故選A.
(10)橢圓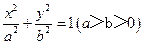 的右焦點為F,其右準線與
的右焦點為F,其右準線與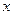 軸的交點為
軸的交點為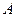 .在橢圓上存在點P滿足線段AP的垂直平分線過點F,則橢圓離心率的取值范圍是
.在橢圓上存在點P滿足線段AP的垂直平分線過點F,則橢圓離心率的取值范圍是
(A)(0,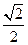 ] (B)(0,
] (B)(0,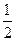 ](C)[
](C)[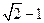 ,1) (D)[
,1) (D)[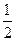 ,1)
,1)
10. 答案D

(A)1(B)2(C)3(D)4
11. 答案D
【命題意圖】本題主要考查利用均值不等式及變形公式求最值.
【解析】原式= 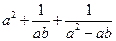 =
= 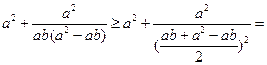
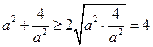 ,當且僅當
,當且僅當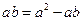 且
且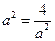 即
即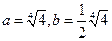 取等號.故選D.
取等號.故選D.
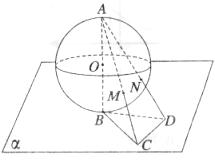
(12)半徑為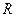 的球
的球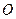 的直徑
的直徑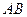 垂直于平面
垂直于平面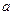 ,垂足為
,垂足為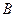 ,
,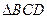 是平面
是平面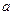 內邊長為
內邊長為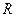 的正三角形,線段
的正三角形,線段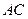 、
、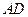 分別與球面交于點
分別與球面交于點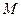 、
、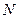 ,那么
,那么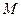 、
、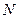 兩點間的球面距離是
兩點間的球面距離是
(A)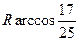 (B)
(B)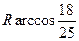
 (C)
(C)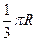 (D)
(D)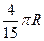
12.A 【命題意圖】本題主要考查球面性質與距離問題.
【解析】連接BM,BN,連接MN,則BM⊥AC,BN⊥BD,由已知直角△ABC與直角△ABD全等,在直角三角形中由等面積法,可得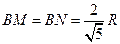 ,∴
,∴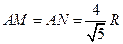 ,
,
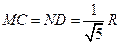 ,∴MN∥CD,且
,∴MN∥CD,且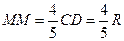 ,在三角形MON中,ON=OM=R,由余弦定理,
,在三角形MON中,ON=OM=R,由余弦定理,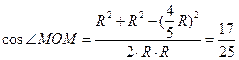 ,∴
,∴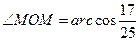 ,∴MN兩點的球面距離為
,∴MN兩點的球面距離為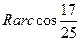 ,故選A
,故選A
二、填空題
(13)(x-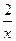 )4的展開式中的常數項為______________(用數字作答)
)4的展開式中的常數項為______________(用數字作答)
13.24 【命題意圖】本題主要考查二項展開式的通項公式和常數項的求法.
【解析】常數項是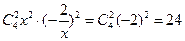 .
.
(14)直線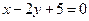 與圓
與圓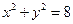 相交于A、B兩點,則
相交于A、B兩點,則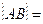 .
.
14. 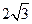 【命題意圖】本題主要考查直線與圓的位置關系.
【命題意圖】本題主要考查直線與圓的位置關系.
【解析】圓心到直線的距離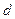 為
為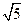 ,又半徑
,又半徑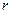 為
為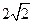 ,∴
,∴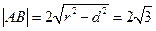 .
.
(15)如圖,二面角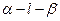 的大小是60°,線段
的大小是60°,線段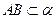 .
.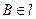 ,
,
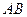 與
與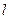 所成的角為30°.則
所成的角為30°.則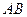 與平面
與平面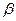 所成的角的正弦值是.
所成的角的正弦值是.
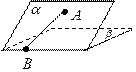
15. 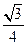 【命題意圖】本題主要考查線線角、線面角、二面角問題,考查空間推理計算能力.
【命題意圖】本題主要考查線線角、線面角、二面角問題,考查空間推理計算能力.
【解析】過A作AO垂直于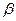 于O,AN⊥
于O,AN⊥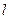 于N,連接ON,OB,則
于N,連接ON,OB,則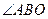 為所求,
為所求,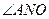 為二面角的平面角,∴
為二面角的平面角,∴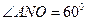 ,設AN的長為
,設AN的長為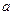 ,則
,則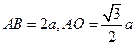 ,∴
,∴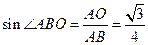 .
.
(16)設S為實數集R的非空子集.若對任意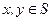 ,都有
,都有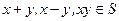 ,則稱S為封閉集。下列命題:
,則稱S為封閉集。下列命題:
1集合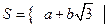
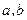 為整數
為整數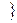 為封閉集;
為封閉集;
2若S為封閉集,則一定有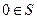 ;
;
3封閉集一定是無限集;
4若S為封閉集,則滿足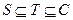 的任意集合
的任意集合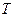 也是封閉集.
也是封閉集.
其中真命題是(寫出所有真命題的序號)
 則
則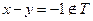 ,所以T不是封閉集.故填①②.
,所以T不是封閉集.故填①②.
三、解答題:本大題共6小題,共74分。解答應寫出文字說明,證明過程或演算步驟。
(17)(本小題滿分12分)
某種有獎銷售的飲料,瓶蓋內印有“獎勵一瓶”或“謝謝購買”字樣,購買一瓶若其瓶蓋內印有“獎勵一瓶”字樣即為中獎,中獎概率為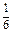 .甲、乙、丙三位同學每人購買了一瓶該飲料。
.甲、乙、丙三位同學每人購買了一瓶該飲料。
(Ⅰ)求三位同學都沒有中獎的概率;
(Ⅱ)求三位同學中至少有兩位沒有中獎的概率.
【命題意圖】本題主要考查相互獨立事件、互斥事件等概率的計算,考查運用所學知識與方法解決實際問題的能力.
解:(Ⅰ)設甲、乙、丙中獎的事件分別為A、B、C,那么
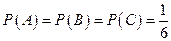 .
.
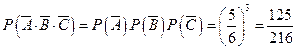 .
.
答:三位同學都沒有中獎的概率是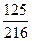 .…………………………………………(6分)
.…………………………………………(6分)
(Ⅱ)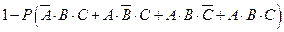
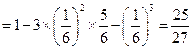 .
.
或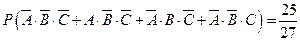 .
.
答:三位同學中至少有兩位沒有中獎的概率為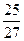 .……………………………(12分)
.……………………………(12分)












