(18)(本小題滿分12分)
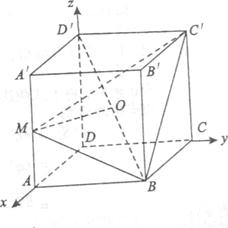
在正方體ABCD-A′B′C′D′中,點M是棱AA′的中點,點O是對角線BD′的中點.
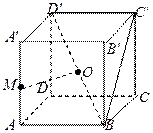
(Ⅰ)求證:OM為異面直線AA′和BD′的公垂線;
(Ⅱ)求二面角M-BC′-B′的大小;
【命題意圖】本題以正方體為載體,考查空間垂直關系的證明以及二面角的計算,考查基本的空間推理與計算能力,考查利用向量解決立體幾何的能力.
解法一
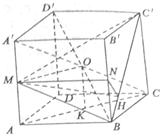
(Ⅰ)連結AC,取AC的中點K,則K為BD的中點,連結OK.
因為點M是棱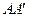 ′的中點,點O是
′的中點,點O是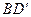 的中點,
的中點,
所以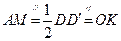 ,
,
所以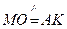 .
.
由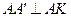 ,得
,得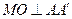
因為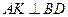 ,
,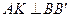 ,所以
,所以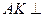 平面
平面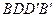 ,
,
所以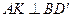 .
.
所以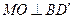 .
.
又因為OM與異面直線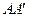 和
和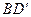 都相交,
都相交,
故OM為異面直線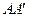 和
和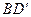 ’的公垂線.……………(5分)
’的公垂線.……………(5分)
(Ⅱ)取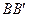 的中點N,連結MN,則
的中點N,連結MN,則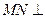 平面
平面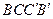 .過點N作
.過點N作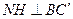 于H,連結MH,則由三垂線定理得,
于H,連結MH,則由三垂線定理得,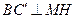 .從而,
.從而,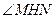 為二面角
為二面角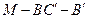 的平面角.
的平面角.
設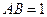 ,則
,則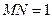 ,
,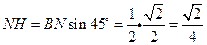 .
.
在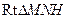 中,
中,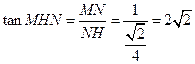 .
.
故二面角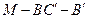 的大小為
的大小為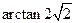 .……………………………(12分)
.……………………………(12分)
解法二
以點D為坐標原點,建立如圖所示的空間直角坐標系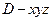 .設
.設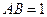 ,則
,則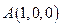 ,
,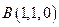 ,
,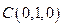 ,
,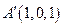 ,
,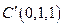 ,
,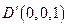 .
.

(Ⅱ)設平面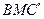 的一個法向量為
的一個法向量為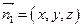 .
.
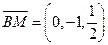 ,
,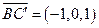 .
.
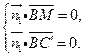 即
即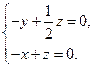
取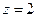 ,則
,則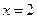 ,
,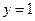 .從而
.從而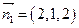 .
.
取平面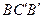 的一個法向量為
的一個法向量為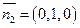 .
.
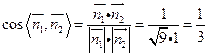 .
.
由圖可知,二面角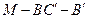 的平面角為銳角,
的平面角為銳角,
故二面角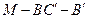 的大小為
的大小為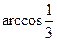 .……………………………(12分)
.……………………………(12分)
【點評】空間的線線垂直的證明方法主要有:(1)定義法;(2)等腰三角形的性質;(3)三垂線定理;(4)線面垂直;(5)向量法.幾何法確定二面角的平面角的方法:(1)直接法;(2)三垂線法;(3)棱的垂面法等,當然如果題目適合建立空間直角坐標系,用向量法更簡潔,但對于分步給分的立體幾何解答題,傳統法也有它的長處.
(19)(本小題滿分12分)
(Ⅰ)1證明兩角和的余弦公式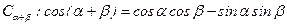 ;
;
2由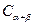 推導兩角和的正弦公式
推導兩角和的正弦公式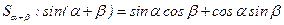 .
.
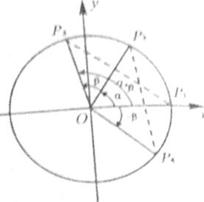
(Ⅱ)已知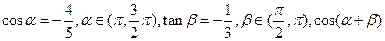 ,求
,求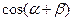
【命題意圖】本題主要考查兩角和的正、余弦公式、誘導公式、同角三角函數的關系等基礎知識及運算能力.
解:(Ⅰ)①如圖,在直角坐標系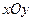 內作單位圓O,并作出角
內作單位圓O,并作出角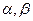 與
與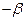 ,使角
,使角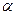 的始邊為
的始邊為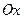 ,交
,交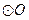 于點
于點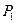 ,終邊交
,終邊交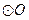 于點
于點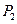 ;角
;角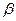 的始邊為
的始邊為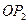 ,終邊交
,終邊交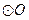 于點
于點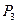 ,角
,角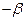 的始邊為
的始邊為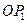 ,終邊交
,終邊交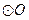 于點
于點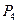 .
.
則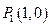 ,
,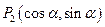 ,
,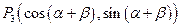 ,
,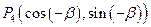 .
.
由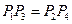 及兩點間的距離公式,得
及兩點間的距離公式,得
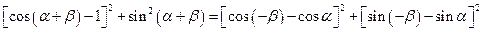
展開并整理,得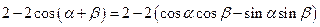 .
.
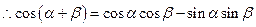 .……………(4分)
.……………(4分)
②由①易得,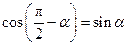 ,
,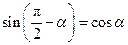 .
.
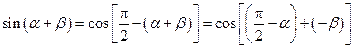
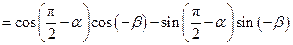
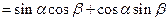 .
.
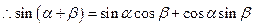 .……………………………(6分)
.……………………………(6分)
(Ⅱ)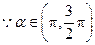 ,
,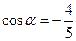 .
.
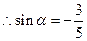 .
.
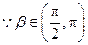 ,
,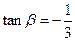 .
.
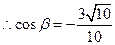 ,
,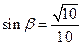 .
.
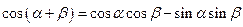
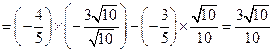 .………………………(12分)
.………………………(12分)












