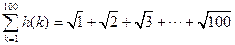19.(本小題共l2分)
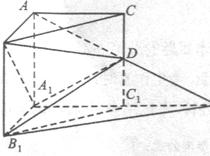
如圖,在直三棱柱AB-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一
P是AD的延長線與A1C1的延長線的交點,且PB1∥平面BDA.
(I)求證:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求點C到平面B1DP的距離.
解析:(1)連接 交
交 于
于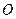 ,
,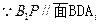 ,
,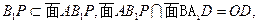
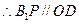 ,又
,又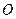 為
為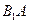 的中點,
的中點,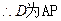 中點,
中點,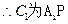 ,
,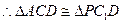
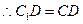 ,D為
,D為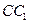 的中點。
的中點。
(2)由題意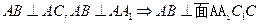 ,過B 作
,過B 作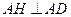 ,連接
,連接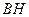 ,則
,則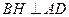 ,
,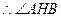 為二面角
為二面角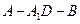 的平面角。在
的平面角。在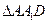 中,
中,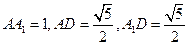 ,則
,則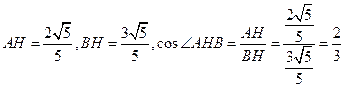
(3)因為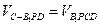 ,所以
,所以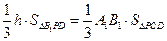 ,
,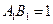
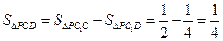 ,
,
在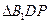 中,
中,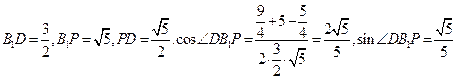 ,
,
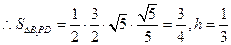
20.(本小題共12分)
設 為非零實數(shù),
為非零實數(shù),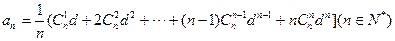
(1)寫出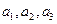 并判斷
并判斷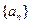 是否為等比數(shù)列。若是,給出證明;若不是,說明理由;
是否為等比數(shù)列。若是,給出證明;若不是,說明理由;
(II)設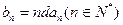 ,求數(shù)列
,求數(shù)列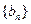 的前n項和
的前n項和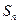 .
.
解析:(1)
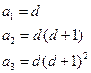
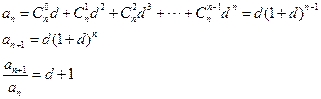
因為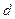 為常數(shù),所以
為常數(shù),所以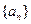 是以
是以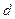 為首項,
為首項,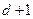 為公比的等比數(shù)列。
為公比的等比數(shù)列。
(2)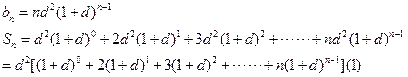
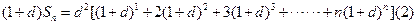
(2)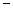 (1)
(1)
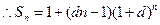
21.(本小題共l2分)
橢圓有兩頂點A(-1,0)、B(1,0),過其焦點F(0,1)的直線l與橢圓交于C、D兩點,并與x軸交于點P.直線AC與直線BD交于點Q.
(I)當|CD | = 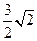 時,求直線l的方程;
時,求直線l的方程;
(II)當點P異于A、B兩點時,求證: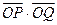 為定值。
為定值。
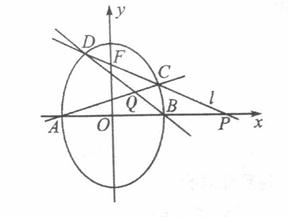
解析:由已知可得橢圓方程為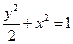 ,設
,設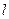 的方程為
的方程為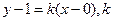 為
為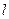 的斜率。
的斜率。
則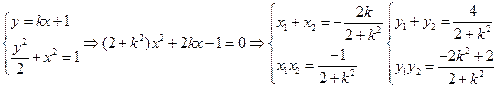
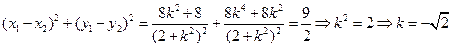
 的方程為
的方程為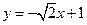
22.(本小題共l4分)
已知函數(shù)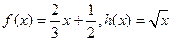
(I)設函數(shù)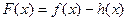 ,求
,求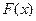 的單調(diào)區(qū)間與極值;
的單調(diào)區(qū)間與極值;
(Ⅱ)設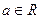 ,解關(guān)于
,解關(guān)于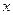 的方程
的方程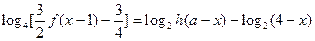
(Ⅲ)試比較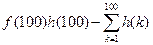 與
與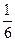 的大小.
的大小.
22、解析:
(1)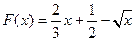 ,
,
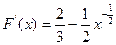
令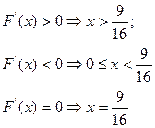
所以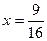 是其極小值點,極小值為
是其極小值點,極小值為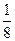 。
。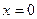 是其極大值點,極大值為
是其極大值點,極大值為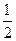
(2)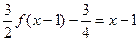 ;
;
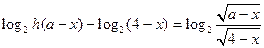
由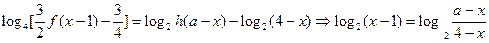
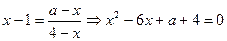
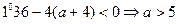 時方程無解
時方程無解
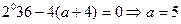 時
時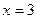
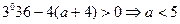 方程的根為
方程的根為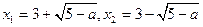
(3)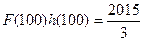 ,
,