評論
打印
18.（本小題滿分13分）
如圖，在長方體ABCD-A1B1C1D1中AA1=AD=1，E為CD中點。
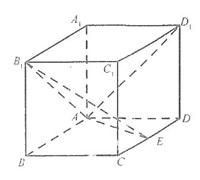
（Ⅰ）求證：B1E⊥A D1
（Ⅱ）在棱AA1上是否存在一點P，使得DP∥平面B1AE？若存在，求AP的行；若存在，求AP的長；若不存在，說明理由。
（Ⅲ）若二面角A-B1E-A1的大小為30°，求AB的長。
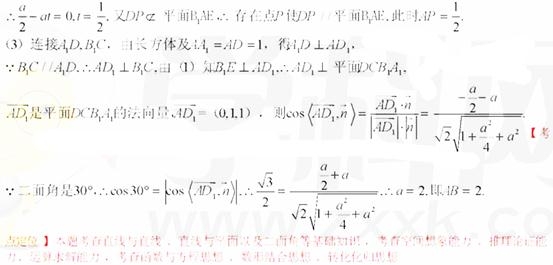
19.（本小題滿分13分）
如圖，橢圓E：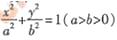
的左焦點為F1，右焦點為F2，離心率
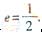。過F1的直線交橢圓于A、B兩點，且△ABF2的周長為8。
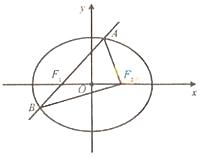
（Ⅰ）求橢圓E的方程。
（Ⅱ）設動直線l：y=kx+m與橢圓E有且只有一個公共點P，且與直線x=4相較于點Q。試探究：在坐標平面內是否存在定點M，使得以PQ為直徑的圓恒過點M？若存在，求出點M的坐標；若不存在，說明理由。
【解析】
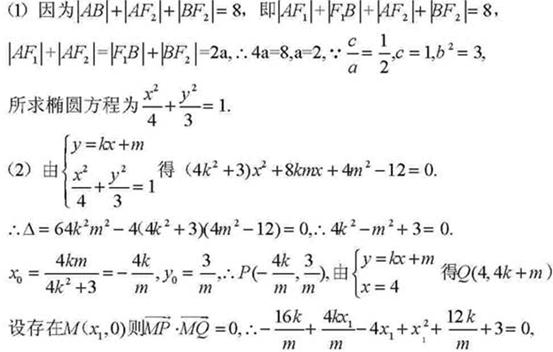
20.（本小題滿分14分）
已知函數f（x）=ex＋ax2-ex，a∈R。
（Ⅰ）若曲線y=f（x）在點（1，f（1））處的切線平行于x軸，求函數f（x）的單調區間；
（Ⅱ）試確定a的取值范圍，使得曲線y=f（x）上存在唯一的點P，曲線在該點處的切線與曲線只有一個公共點P。
21.本題設有（1）、（2）、（3）三個選考題，每題7分，請考生任選2題作答，滿分14分。如果多做，則按所做的前兩題計分。作答時，先用2B鉛筆在答題卡上把所選題目對應題號右邊的方框圖黑，并將所選題號填入括號中。
（1）（本小題滿分7分）選修4-2：矩陣與變換
設曲線2x2+2xy+y2=1在矩陣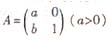
對應的變換作用下得到的曲線為x2+y2=1。
（Ⅰ）求實數a，b的值。
（Ⅱ）求A2的逆矩陣。
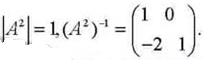
【考點定位】本題主要考查矩陣與變換等基礎知識，考查運算求解能力，考查轉化化歸思想.
（2）（本小題滿分7分）選修4-4：坐標系與參數方程
在平面直角坐標系中，以坐標原點O為幾點，x軸的正半軸為極軸建立極坐標系。已知直線l上兩點M，N的極坐標分別為（2,0），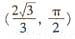
，圓C的參數方程
。
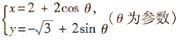（Ⅰ）設P為線段MN的中點，求直線OP的平面直角坐標方程；
（Ⅱ）判斷直線l與圓C的位置關系。
【解析】
（Ⅰ）由題意知M（2,0），N（0，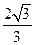
），因為P是線段MN中點，則P（1，
），
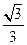因此PO直角坐標方程為：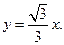
（Ⅱ）因為直線l上兩點M（2,0），N（0，）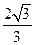
∴l垂直平分線方程為：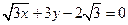
，圓心（2，
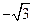），半徑r=2.
∴d=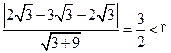
,故直線l和圓C相交.
【考點定位】本題主要考查極坐標與參數方程的互化、圓的參數方程等基礎知識，考查運算求解能力，考查轉化化歸思想。
（3）（本小題滿分7分）選修4-5：不等式選講
已知函數f（x）=m-|x-2|，m∈R，且f（x+2）≥0的解集為[-1,1].
（Ⅰ）求m的值；
（Ⅱ）若a，b，c∈R，且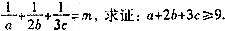
【解析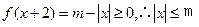】(1)∵
，
∴
的解集是[-1,1]
故m=1.
(2)由（1）知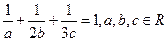
,由柯西不等式得
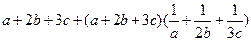
【考點定位】本題主要考查絕對值不等式、柯西不等式等基本知識，考查運算求解能力，考查化歸轉化思想
