第I卷(選擇題 共50分)
一、選擇題:本大題共10小題,每小題5分,共50分。在每小題給出分四個選項中,只有一項是符合題目要求的。
1.若復(fù)數(shù)z滿足zi=1-i,則z等于
A.-1-I B.1-i C.-1+I D.1=i
2.等差數(shù)列{an}中,a1+a5=10,a4=7,則數(shù)列{an}的公差為
A.1 B.2 C.3 D.4
3.下列命題中,真命題是
A. 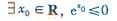 B.
B. 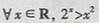
C.a+b=0的充要條件是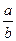 =-1 D.a>1,b>1是ab>1的充分條件
=-1 D.a>1,b>1是ab>1的充分條件
4.一個幾何體的三視圖形狀都相同、大小均相等,那么這個幾何體不可以是
A.球 B.三棱柱 C.正方形 D.圓柱
5.下列不等式一定成立的是
C. 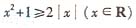 D.
D. 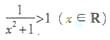
6.如圖所示,在邊長為1的正方形OABC中任取一點P,則點P恰好取自陰影部分的概率為
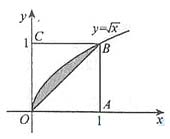
7.設(shè)函數(shù)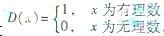 則下列結(jié)論錯誤的是
則下列結(jié)論錯誤的是
A.D(x)的值域為{0,1} B. D(x)是偶函數(shù)
C. D(x)不是周期函數(shù) D. D(x)不是單調(diào)函數(shù)
8.已知雙曲線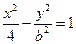 的右焦點與拋物線y2=12x的焦點重合,則該雙曲線的焦點到其漸近線的距離等于
的右焦點與拋物線y2=12x的焦點重合,則該雙曲線的焦點到其漸近線的距離等于
9.若函數(shù)y=2x圖像上存在點(x,y)滿足約束條件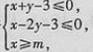 ,則實數(shù)m的最大值為
,則實數(shù)m的最大值為
10.函數(shù)f(x)在[a,b]上有定義,若對任意x1,x2∈[a,b],有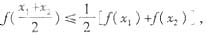 則稱f(x)在[a,b]上具有性質(zhì)P。設(shè)f(x)在[1,3]上具有性質(zhì)P,現(xiàn)給出如下命題:
則稱f(x)在[a,b]上具有性質(zhì)P。設(shè)f(x)在[1,3]上具有性質(zhì)P,現(xiàn)給出如下命題:
①f(x)在[1,3]上的圖像時連續(xù)不斷的;
②f(x2)在[1,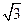 ]上具有性質(zhì)P;
]上具有性質(zhì)P;
③若f(x)在x=2處取得最大值1,則f(x)=1,x∈[1,3];
④對任意x1,x2,x3,x4∈[1,3],有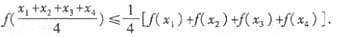
其中真命題的序號是
A.①② B.①③ C.②④ D.③④
第Ⅱ卷(非選擇題共100分)
二、填空題:本大題共5小題,每小題4分,共20分,把答案填在答題卡的相應(yīng)位置。
11.(a+x)4的展開式中x3的系數(shù)等于8,則實數(shù)a=_________。
12.閱讀右圖所示的程序框圖,運行相應(yīng)地程序,輸出的s值等于_____________________。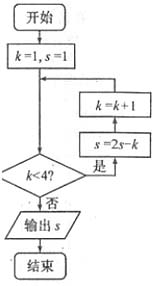
13.已知△ABC得三邊長成公比為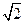 的等比數(shù)列,則其最大角的余弦值為_________.
的等比數(shù)列,則其最大角的余弦值為_________.
14.數(shù)列{an}的通項公式 ,前n項和為Sn,則S2012=___________。
,前n項和為Sn,則S2012=___________。
15.對于實數(shù)a和b,定義運算“﹡”: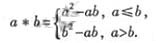
設(shè)f(x)=(2x-1)﹡(x-1),且關(guān)于x的方程為f(x)=m(m∈R)恰有三個互不相等的實數(shù)根x1,x2,x3,則x1x2x3的取值范圍是_________________。
三、解答題:本大題共6小題,共80分,解答題寫出文字說明,證明過程或演算步驟。
16.(本小題滿分13分)
受轎車在保修期內(nèi)維修費等因素的影響,企業(yè)生產(chǎn)每輛轎車的利潤與該轎車首次出現(xiàn)故障的時間有關(guān),某轎車制造廠生產(chǎn)甲、乙兩種品牌轎車,保修期均為2年,現(xiàn)從該廠已售出的兩種品牌轎車中隨機抽取50輛,統(tǒng)計書數(shù)據(jù)如下:
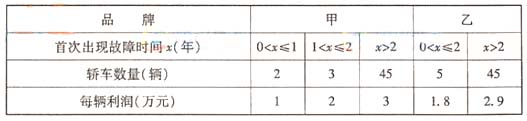
將頻率視為概率,解答下列問題:
(I)從該廠生產(chǎn)的甲品牌轎車中隨機抽取一輛,求首次出現(xiàn)故障發(fā)生在保修期內(nèi)的概率;
(II)若該廠生產(chǎn)的轎車均能售出,記住生產(chǎn)一輛甲品牌轎車的利潤為X1,生產(chǎn)一輛乙品牌轎車的利潤為X2,分別求X1,X2的分布列;
(III)該廠預(yù)計今后這兩種品牌轎車銷量相當(dāng),由于資金限制,只能生產(chǎn)其中一種品牌轎車,若從經(jīng)濟效益的角度考慮,你認(rèn)為應(yīng)該產(chǎn)生哪種品牌的轎車?說明理由。
17(本小題滿分13分)
某同學(xué)在一次研究性學(xué)習(xí)中發(fā)現(xiàn),以下五個式子的值都等于同一個常數(shù)。
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°- sin2(-18°)cos48°
(5)sin2(-25°)+cos255°- sin2(-25°)cos55°
Ⅰ 試從上述五個式子中選擇一個,求出這個常數(shù)
Ⅱ 根據(jù)(Ⅰ)的計算結(jié)果,將該同學(xué)的發(fā)現(xiàn)推廣位三角恒等式,并證明你的結(jié)論。
18.(本小題滿分13分)
如圖,在長方體ABCD-A1B1C1D1中AA1=AD=1,E為CD中點。
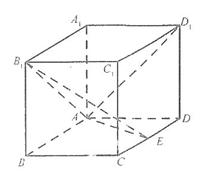
(Ⅰ)求證:B1E⊥A D1
(Ⅱ)在棱AA1上是否存在一點P,使得DP∥平面B1AE?若存在,求AP的行;若存在,求AP的長;若不存在,說明理由。(Ⅲ)若二面角A-B1E-A1的大小為30°,求AB的長。


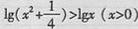 B.
B. 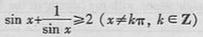
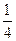 B.
B. 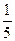
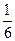 D.
D. 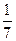
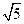
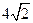 C.3 D.5
C.3 D.5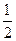 B.1 C.
B.1 C.