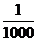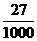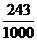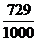第二部分 (非選擇題 共90分)
二、填空題(本大題共4個小題,每小題4分,共16分。把答案填在答題紙的相應(yīng)位置上。)
13、設(shè)全集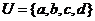 ,集合
,集合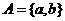 ,
,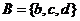 ,則
,則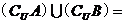 _______。
_______。
[答案]{a, c, d}
[解析]∵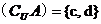 ;
;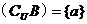 ∴
∴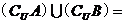 {a,c,d}
{a,c,d}
[點評]本題難度較低,只要稍加注意就不會出現(xiàn)錯誤.
14、如圖,在正方體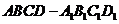 中,
中,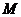 、
、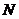 分別是
分別是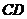 、
、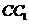 的中點,則異面直線
的中點,則異面直線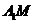 與
與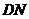 所成角的大小是____________。
所成角的大小是____________。

[答案]90º
[解析]方法一:連接D1M,易得DN⊥A1D1 ,DN⊥D1M,
所以,DN⊥平面A1MD1,
又A1M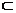 平面A1MD1,所以,DN⊥A1D1,故夾角為90º
平面A1MD1,所以,DN⊥A1D1,故夾角為90º
方法二:以D為原點,分別以DA, DC, DD1為x, y, z軸,建立空間直角坐標系D—xyz.設(shè)正方體邊長為2,則D(0,0,0),N(0,2,1),M(0,1,0)A1(2,0,2)
故,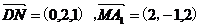
所以,cos<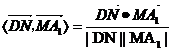 = 0,故DN⊥D1M,所以夾角為90º
= 0,故DN⊥D1M,所以夾角為90º
[點評]異面直線夾角問題通常可以采用兩種途徑: 第一,把兩條異面直線平移到同一平面中借助三角形處理; 第二,建立空間直角坐標系,利用向量夾角公式解決.
15、橢圓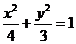 的左焦點為
的左焦點為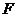 ,直線
,直線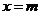 與橢圓相交于點
與橢圓相交于點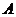 、
、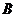 ,當
,當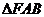 的周長最大時,
的周長最大時,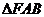 的面積是____________。
的面積是____________。
[答案] 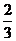
[解析]根據(jù)橢圓定義知:4a=12, 得a=3 , 又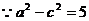
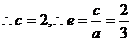
[點評]本題考查對橢圓概念的掌握程度.突出展現(xiàn)高考前的復(fù)習要回歸課本的新課標理念.
16、記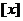 為不超過實數(shù)
為不超過實數(shù)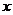 的最大整數(shù),例如,
的最大整數(shù),例如,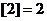 ,
,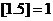 ,
,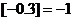 。設(shè)
。設(shè)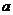 為正整數(shù),數(shù)列
為正整數(shù),數(shù)列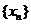 滿足
滿足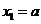 ,
,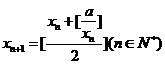 ,現(xiàn)有下列命題:
,現(xiàn)有下列命題:
①當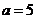 時,數(shù)列
時,數(shù)列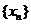 的前3項依次為5,3,2;
的前3項依次為5,3,2;
②對數(shù)列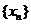 都存在正整數(shù)
都存在正整數(shù)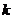 ,當
,當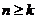 時總有
時總有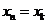 ;
;
③當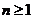 時,
時,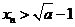 ;
;
④對某個正整數(shù)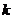 ,若
,若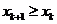 ,則
,則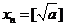 。
。
其中的真命題有____________。(寫出所有真命題的編號)
[答案]①③④
[解析]若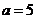 ,根據(jù)
,根據(jù)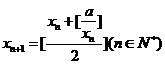
當n=1時,x2=[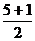 ]=3, 同理x3=
]=3, 同理x3=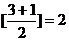 , 故①對.
, 故①對.
對于②③④可以采用特殊值列舉法:
當a=1時,x1=1, x2=1, x3=1, ……xn=1, …… 此時②③④均對.
當a=2時,x1=2, x2=1, x3=1, ……xn=1, …… 此時②③④均對
當a=3時,x1=3, x2=2, x3=1, x4=2……xn=1, ……此時③④均對
綜上,真命題有 ①③④ .
[點評]此題難度較大,不容易尋找其解題的切入點,特殊值列舉是很有效的解決辦法.
三、解答題(本大題共6個小題,共74分。解答應(yīng)寫出必要的文字說明,證明過程或演算步驟。)
17、(本小題滿分12分)
某居民小區(qū)有兩個相互獨立的安全防范系統(tǒng)(簡稱系統(tǒng))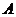 和
和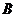 ,系統(tǒng)
,系統(tǒng)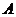 和
和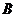 在任意時刻發(fā)生故障的概率分別為
在任意時刻發(fā)生故障的概率分別為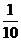 和
和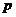 。
。
(Ⅰ)若在任意時刻至少有一個系統(tǒng)不發(fā)生故障的概率為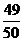 ,求
,求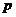 的值;
的值;
(Ⅱ)設(shè)系統(tǒng)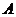 在3次相互獨立的檢測中不發(fā)生故障的次數(shù)為隨機變量
在3次相互獨立的檢測中不發(fā)生故障的次數(shù)為隨機變量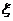 ,求
,求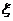 的概率分布列及數(shù)學期望
的概率分布列及數(shù)學期望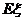 。
。
[解析](1)設(shè):“至少有一個系統(tǒng)不發(fā)生故障”為事件C,那么
1-P(C)=1-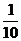 P=
P=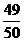 ,解得P=
,解得P=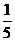 ………………………………4 分
………………………………4 分
(2)由題意,P(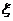 =0)=
=0)=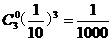
P(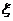 =1)=
=1)=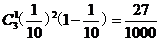
P(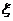 =2)=
=2)=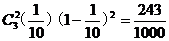
P(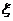 =3)=
=3)=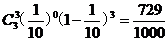
所以,隨機變量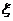 的概率分布列為:
的概率分布列為:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
故隨機變量X的數(shù)學期望為:
E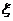 =0
=0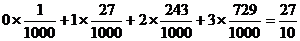 ……………………12分.
……………………12分.
[點評]本小題主要考查相互獨立事件,獨立重復(fù)試驗、互斥事件、隨機變量的分布列、數(shù)學期望等概念及相關(guān)計算,考查運用概率知識與方法解決實際問題的能力.
18、(本小題滿分12分)
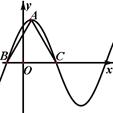
函數(shù)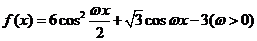 在一個周期內(nèi)的圖象如圖所示,
在一個周期內(nèi)的圖象如圖所示,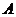 為圖象的最高點,
為圖象的最高點,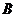 、
、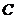 為圖象與
為圖象與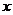 軸的交點,且
軸的交點,且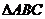 為正三角形。
為正三角形。
(Ⅰ)求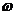 的值及函數(shù)
的值及函數(shù)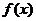 的值域;
的值域;
(Ⅱ)若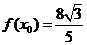 ,且
,且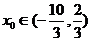 ,求
,求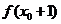 的值。
的值。
[解析](Ⅰ)由已知可得: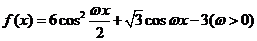
=3cosωx+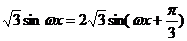
又由于正三角形ABC的高為2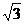 ,則BC=4
,則BC=4
所以,函數(shù)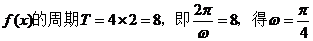
所以,函數(shù)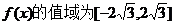 。……………………6分
。……………………6分
(Ⅱ)因為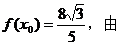 (Ⅰ)有
(Ⅰ)有
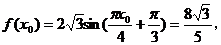
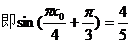
由x0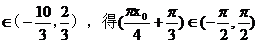
所以,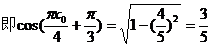
故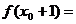
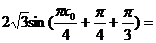
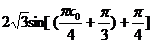
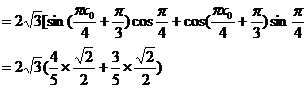
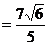 ………………………………………………………12分
………………………………………………………12分
[點評]本題主要考查三角函數(shù)的圖像與性質(zhì)同三角函數(shù)的關(guān)系、兩角和的正(余)弦公式、二倍角公式等基礎(chǔ)知識,考查運算能力,考查樹形結(jié)合、轉(zhuǎn)化等數(shù)學思想.