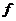19.(本小題滿分13分)某產品按行業生產標準分成8個等級,等級系數X依次為1,2,……,8,其中X≥5為標準A,X≥3為標準B,已知甲廠執行標準A生產該產品,產品的零售價為6元/件;乙廠執行標準B生產該產品,產品的零售價為4元/件,假定甲、乙兩廠得產品都符合相應的執行標準(I)已知甲廠產品的等級系數X1的概率分布列如下所示:
| 5 | 6 | 7 | 8 |
P | 0.4 | a | b | 0.1 |
且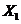 的數字期望
的數字期望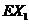 =6,求a,b的值;
=6,求a,b的值;

【解析】:本小題主要考查概率、統計等基礎知識,考查數據處理能力 、運算求解能力、應用意識、考查函數與方程思想、必然與或然思想、分類與整合思想,滿分13分。
、運算求解能力、應用意識、考查函數與方程思想、必然與或然思想、分類與整合思想,滿分13分。
解:(I)因為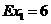 ,所以
,所以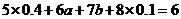 ,即
,即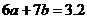 又由
又由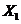 的概率分布列得
的概率分布列得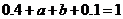 ,即
,即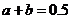 由
由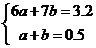 解得
解得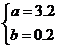
(II)由已知得,樣本的頻率分布表如下:
| 3 | 4 | 5 | 6 | 7 | 8 |
| 0.3 | 0.2 | 0.2 | 0.1 | 0.1 | 0.1 |
用這個樣本的頻率分布估計總體分布,將頻率視為概率,可得等級系數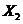 的概率分布列如下:
的概率分布列如下:
| 3 | 4 | 5 | 6 | 7 | 8 |
| 0.3 | 0.2 | 0.2 | 0.1 | 0.1 | 0.1 |
所以
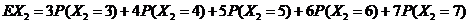
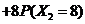 =3×0.3+4×0.2+5×0.2+6×0.1+7×0.1+8×0.1=4.8即乙廠產品的等級系數的數學期望等于4.8。
=3×0.3+4×0.2+5×0.2+6×0.1+7×0.1+8×0.1=4.8即乙廠產品的等級系數的數學期望等于4.8。
(Ⅲ)乙廠的產品更具 可購買性,理由如下:因為甲廠產品的等級系數的數學期望等于6,價格為6元/件,所以其性價比為
可購買性,理由如下:因為甲廠產品的等級系數的數學期望等于6,價格為6元/件,所以其性價比為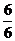 =1,因為乙廠產品的等級系數的數學期望等于4.8,價
=1,因為乙廠產品的等級系數的數學期望等于4.8,價 格為4元/件,所以其性價比為
格為4元/件,所以其性價比為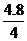 =1.2據此,乙廠的產品更其可購買性。
=1.2據此,乙廠的產品更其可購買性。
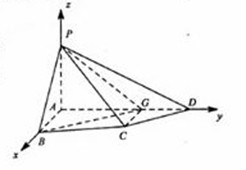
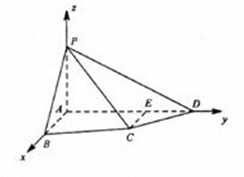
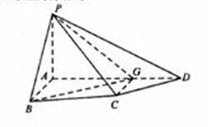
20.(本小題滿分14分) 如圖,四棱錐P-ABCD中,PA⊥底面ABCD,四邊形ABCD中,AB⊥AD,AB+AD=4,CD=
如圖,四棱錐P-ABCD中,PA⊥底面ABCD,四邊形ABCD中,AB⊥AD,AB+AD=4,CD=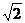 ,
,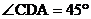 .
.
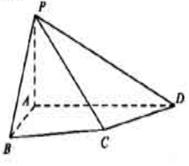
(I)求證:平面PAB⊥平面PAD;(II)設AB=AP.(i)若直線PB與平面PCD所成的角為
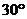 ,求線段AB的長; (ii)在線段AD上是否存在一個點G,使得點G到點P,B,C,D的距離都相等?說明理由。
,求線段AB的長; (ii)在線段AD上是否存在一個點G,使得點G到點P,B,C,D的距離都相等?說明理由。
【解析】:本小題主要考查直線與直線、直線與平面、平面與平面的位置關系等基礎知識,考查空間想象能力、推理論證能力、抽象概括能力、運算求解能力,考查函數與方程思想、數形結合思想、化歸與轉化思想,滿分14分。
法一:(Ⅰ)因為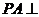 平面
平面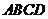 ,
,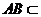 平面
平面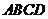 ,所以
,所以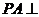
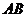 ,又
,又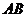
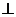
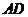 ,
,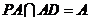 所以
所以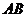
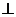 平面
平面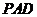 ,又
,又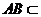 平面
平面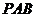 ,所以平面
,所以平面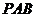
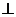 平面
平面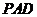
 。
。
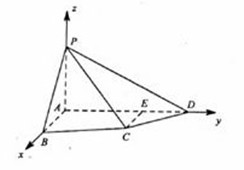
(II)以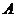 為坐標原點,建立空間直角坐標系
為坐標原點,建立空間直角坐標系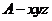 (如圖)在平面
(如圖)在平面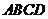 內,作
內,作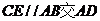 于點
于點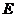 ,
,
則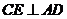 ,在
,在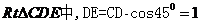
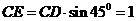 ,設
,設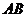 =
=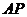 =
=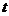 ,
,
則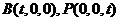 ,由
,由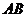 +
+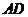 =4得
=4得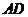 =4-
=4-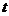 ,
,
所以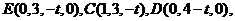
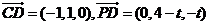
(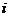 )設平面
)設平面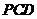 的法向量為
的法向量為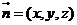 ,由
,由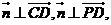 得
得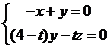
取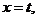 得平面
得平面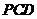 的一個法向量
的一個法向量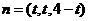 ,又
,又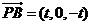 ,故由直線
,故由直線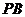 與平面
與平面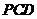 所成的角為
所成的角為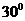 得
得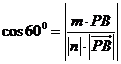 即
即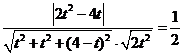 ,解得
,解得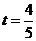 或
或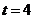 (舍去,因為
(舍去,因為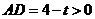 ),所以
),所以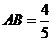
(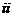 )假設在線段
)假設在線段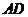 上存在一個點C,使得點
上存在一個點C,使得點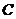 到點
到點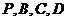 的距離都相等。
的距離都相等。
由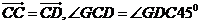 ,從而
,從而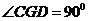 ,即
,即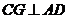 ,
,
所以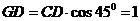 設
設 ,則
,則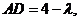
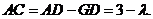
在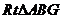 中,
中,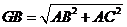
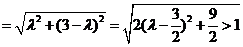 ,
,
這與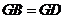 矛盾,所以在線段
矛盾,所以在線段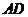 上不存在一個點
上不存在一個點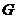 ,使得點
,使得點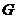 到
到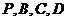 的距離都相等。
的距離都相等。
法二:
(Ⅰ)同解法一
(II)( )以
)以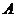 為坐標原點,建立空間直角坐標系
為坐標原點,建立空間直角坐標系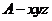 (如圖)在平面
(如圖)在平面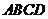 內,作
內,作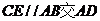 于點E,
于點E,
則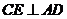 ,在
,在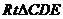 中,
中,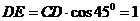
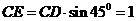 ,設
,設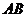 =
=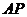 =
=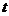 ,
,
則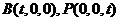 ,由
,由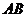 +
+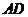 =4得
=4得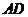 =4-
=4-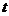 ,
,
所以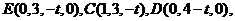
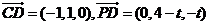

(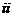 )假設在線段
)假設在線段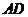 上存在一個點C,使得點
上存在一個點C,使得點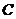 到點
到點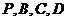 的距離都相等。
的距離都相等。
 由
由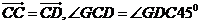 ,
,
從而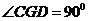 ,即
,即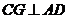 ,
,
所以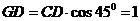
設 ,則
,則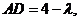
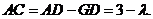 在
在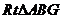 中,
中,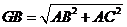
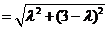
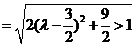 ,這與
,這與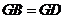 矛盾,所以在線段
矛盾,所以在線段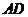 上不存在一個點
上不存在一個點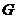 ,使得點
,使得點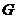 到
到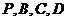 的距離都相等。
的距離都相等。
21 . 本題設有(1)、(2)、(3)三個選考題,每題7分,請考生任選2題做答,滿分14分,如果多做,則按所做的前兩題計分,做答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中。
. 本題設有(1)、(2)、(3)三個選考題,每題7分,請考生任選2題做答,滿分14分,如果多做,則按所做的前兩題計分,做答時,先用2B鉛筆在答題卡上把所選題目對應的題號涂黑,并將所選題號填入括號中。
(1)(本小題滿分7分)選修4-2:矩陣與變換
設矩陣 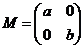 (其中a>0,b>0).(I)若a=2,b=3,求矩陣M的逆矩陣M-1;(II)若曲線C:x2+y2=1在矩陣M所對應的線性變換作用下得到曲線C’:
(其中a>0,b>0).(I)若a=2,b=3,求矩陣M的逆矩陣M-1;(II)若曲線C:x2+y2=1在矩陣M所對應的線性變換作用下得到曲線C’: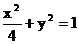 ,求a,b的值.
,求a,b的值.
【解析】:本小題主要考查矩陣與變換等基礎知識,考查運算求解能力,考查化歸與轉化思想,滿分7分。
(Ⅰ)設矩陣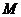 的逆矩陣
的逆矩陣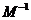 =
=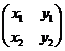 ,則
,則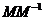 =
=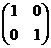
又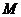 =
=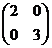 ,所以
,所以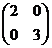
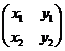 =
=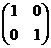
所以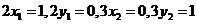 ,即
,即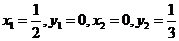 ,
,
故所求的逆矩陣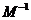 =
=

(Ⅰ)把極坐標系下的點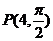 化為直角坐標,得
化為直角坐標,得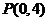 ,因為點
,因為點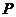 的直角坐標(0,4)滿足直線
的直角坐標(0,4)滿足直線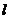 的方程
的方程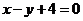 ,所以點
,所以點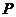 在直線
在直線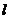 上。
上。
(II)因為點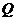 在曲線
在曲線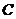 上,故可設點
上,故可設點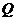 的坐標為
的坐標為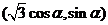 ,從而點
,從而點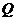 到直線
到直線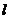 的距離為
的距離為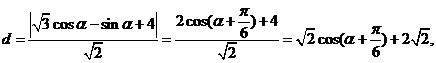
由此得,當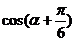 =-1時,
=-1時,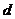 取得最小值,且最小值為
取得最小值,且最小值為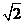
(3)(本小題滿分7分)選修4-5:不等式選講
設不等式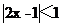 的解集為M.(I)求集合M;(II)若a,b∈M,試比較ab+1與a+b的大小.
的解集為M.(I)求集合M;(II)若a,b∈M,試比較ab+1與a+b的大小.