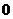20.(本小題滿分12分)如圖,在拋物線 的焦點為
的焦點為 ,準線
,準線 與
與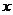 軸的交點為
軸的交點為 .點
.點 在拋物線
在拋物線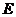 上,以
上,以 為圓心
為圓心 為半徑作圓,設圓
為半徑作圓,設圓 與準線
與準線 的交于不同的兩點
的交于不同的兩點 .
.
(1)若點 的縱坐標為2,求
的縱坐標為2,求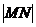 ;
;
(2)若 ,求圓
,求圓 的半徑.
的半徑.

本小題主要考查拋物線的方程、圓的方程與性質、直線與圓的位置關系等基礎知識,考查運算求解能力、推理論證能力,考查函數與方程思想、數形結合思想、化歸與轉化思想.滿分12分.
解:(Ⅰ)拋物線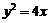 的準線
的準線 的方程為
的方程為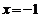 ,
,
由點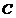 的縱坐標為
的縱坐標為 ,得點
,得點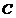 的坐標為
的坐標為
所以點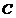 到準線
到準線 的距離
的距離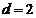 ,又
,又 .
.
所以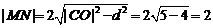 .
.
(Ⅱ)設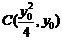 ,則圓
,則圓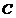 的方程為
的方程為 ,
,
即 .
.
由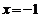 ,得
,得
設 ,
,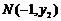 ,則:
,則:

由 ,得
,得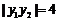
所以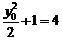 ,解得
,解得 ,此時
,此時
所以圓心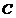 的坐標為
的坐標為 或
或
從而 ,
, ,即圓
,即圓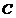 的半徑為
的半徑為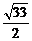
21(本小題滿分12分)如圖,在等腰直角三角形 中,
中,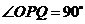 ,
, ,點
,點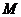 在線段
在線段 上.
上.
(1)若 ,求
,求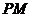 的長;
的長;
(2)若點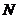 在線段
在線段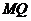 上,且
上,且 ,問:當
,問:當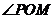 取何值時,
取何值時, 的面積最小?并求出面積的最小
的面積最小?并求出面積的最小
值.

本小題主要考查解三角形、同角三角函數的基本關系、兩角和與差的三角函數等基礎知識,考查推理論證能力、抽象概括能力、運算求解能力,考查函數與方程思想、數形結合思想、化歸與轉化思想.滿分12分.
解:(Ⅰ)在 中,
中, ,
, ,
, ,
,
由余弦定理得, ,
,
得 ,
,
解得 或
或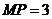 .
.
(Ⅱ)設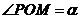 ,
, ,
,
在 中,由正弦定理,得
中,由正弦定理,得 ,
,
所以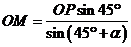 ,
,
同理
故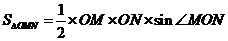
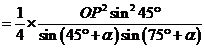

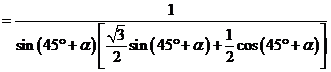
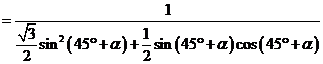



因為 ,
, ,所以當
,所以當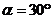 時,
時, 的最大值為
的最大值為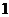 ,此時
,此時 的面積取到最小值.即2
的面積取到最小值.即2 時,
時, 的面積的最小值為
的面積的最小值為 .
.
22(本小題滿分14分)已知函數 (
( ,
, 為自然對數的底數).
為自然對數的底數).
(1)若曲線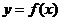 在點
在點 處的切線平行于
處的切線平行于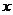 軸,求
軸,求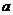 的值;
的值;
(2)求函數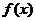 的極值;
的極值;
(3)當 的值時,若直線
的值時,若直線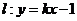 與曲線
與曲線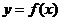 沒有公共點,求
沒有公共點,求 的最大值.
的最大值.
本小題主要考查函數與導數,函數的單調性、極值、零點等基礎知識,考查推理論證能力、運算求解能力,考查函數與方程思想、數形結合思想、分類與整合思想、化歸與轉化思想.滿分14分.
解:(Ⅰ)由 ,得
,得 .
.
又曲線 在點
在點 處的切線平行于
處的切線平行于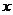 軸,
軸,
得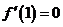 ,即
,即 ,解得
,解得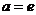 .
.
(Ⅱ) ,
,
①當 時,
時, ,
, 為
為 上的增函數,所以函數
上的增函數,所以函數 無極值.
無極值.
②當 時,令
時,令 ,得
,得 ,
,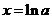 .
.
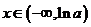 ,
,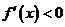 ;
; ,
, .
.
所以 在
在 上單調遞減,在
上單調遞減,在 上單調遞增,
上單調遞增,
故 在
在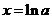 處取得極小值,且極小值為
處取得極小值,且極小值為 ,無極大值.
,無極大值.
綜上,當 時,函數
時,函數 無極小值;
無極小值;
當 ,
, 在
在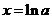 處取得極小值
處取得極小值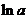 ,無極大值.
,無極大值.
(Ⅲ)當 時,
時,
令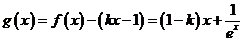 ,
,
則直線 :
: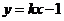 與曲線
與曲線 沒有公共點,
沒有公共點,
等價于方程 在
在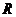 上沒有實數解.
上沒有實數解.
假設 ,此時
,此時 ,
,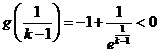 ,
,
又函數 的圖象連續不斷,由零點存在定理,可知
的圖象連續不斷,由零點存在定理,可知 在
在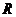 上至少有一解,與“方程
上至少有一解,與“方程 在
在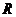 上沒有實數解”矛盾,故
上沒有實數解”矛盾,故 .
.
又 時,
時, ,知方程
,知方程 在
在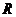 上沒有實數解.
上沒有實數解.
所以 的最大值為
的最大值為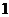 .
.
解法二:
(Ⅰ)(Ⅱ)同解法一.
(Ⅲ)當 時,
時, .
.
直線 :
: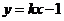 與曲線
與曲線 沒有公共點,
沒有公共點,
等價于關于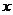 的方程
的方程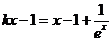 在
在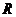 上沒有實數解,即關于
上沒有實數解,即關于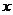 的方程:
的方程:
 (*)
(*)
在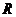 上沒有實數解.
上沒有實數解.
①當 時,方程(*)可化為
時,方程(*)可化為 ,在
,在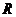 上沒有實數解.
上沒有實數解.
②當 時,方程(*)化為
時,方程(*)化為 .
.
令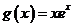 ,則有
,則有 .
.
令 ,得
,得 ,
,
當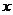 變化時,
變化時,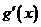 的變化情況如下表:
的變化情況如下表:
|
|
|
|
|
|
|
|
|
|
|
|
當 時,
時, ,同時當
,同時當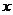 趨于
趨于 時,
時, 趨于
趨于 ,
,
從而 的取值范圍為
的取值范圍為 .
.
所以當 時,方程(*)無實數解,
時,方程(*)無實數解,
解得 的取值范圍是
的取值范圍是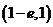 .
.
綜上,得 的最大值為
的最大值為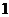 .
.