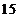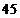三.解答題
17.(本小題滿分12分)已知等差數列 的公差
的公差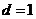 ,前
,前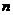 項和為
項和為 .
.
(1)若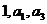 成等比數列,求
成等比數列,求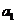 ;
;
(2)若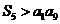 ,求
,求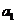 的取值范圍.
的取值范圍.
本小題主要考查等比等差數列、等比數列和不等式等基礎知識,考查運算求解能力,考查函數與方程思想、化歸與轉化思想.滿分12分.
解:(1)因為數列 的公差
的公差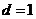 ,且
,且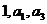 成等比數列,
成等比數列,
所以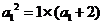 ,
,
即 ,解得
,解得 或
或 .
.
(2)因為數列 的公差
的公差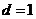 ,且
,且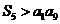 ,
,
所以 ;
;
即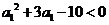 ,解得
,解得
18.(本小題滿分12分)如圖,在四棱錐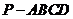 中,
中,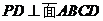 ,
, ,
, ,
, ,
, ,
,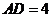 ,
, .
.
(1)當正視圖方向與向量 的方向相同時,畫出四棱錐
的方向相同時,畫出四棱錐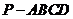 的正視圖.(要求標出尺寸,并畫出演算過程);
的正視圖.(要求標出尺寸,并畫出演算過程);
(2)若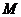 為
為 的中點,求證:
的中點,求證: ;
;
(3)求三棱錐 的體積.
的體積.

本小題主要考查直線與直線、直線與平面的位置關系及幾何體的三視圖和體積等基礎知識,考查空間想象能力,推理論證能力.運算求解能力,考查數形結合能力、化歸與轉化思想,滿分12分.
解法一:
(Ⅰ)在梯形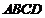 中,過點
中,過點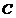 作
作 ,垂足為
,垂足為 ,
,
由已知得,四邊形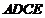 為矩形,
為矩形,
在 中,由
中,由 ,
, ,依勾股定理得:
,依勾股定理得:
 ,從而
,從而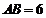
又由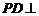 平面
平面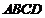 得,
得,
 從而在
從而在 中,由
中,由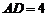 ,
, ,得
,得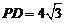
正視圖如右圖所示:
(Ⅱ)取 中點
中點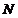 ,連結
,連結 ,
,
在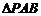 中,
中, 是
是 中點,
中點,
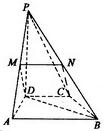
∴ ,
, ,又
,又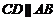 ,
,
∴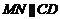 ,
,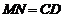
∴四邊形 為平行四邊形,∴
為平行四邊形,∴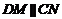
又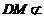 平面
平面 ,
, 平面
平面
∴ 平面
平面
(Ⅲ)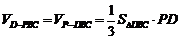
又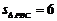 ,
,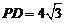 ,所以
,所以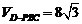
解法二:
(Ⅰ)同解法一

(Ⅱ)取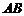 的中點
的中點 ,連結
,連結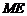 ,
,
在梯形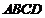 中,
中, ,且
,且
∴四邊形 為平行四邊形
為平行四邊形
∴ ,又
,又 平面
平面 ,
, 平面
平面
∴ 平面
平面 ,又在
,又在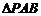 中,
中,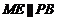
 平面
平面 ,
, 平面
平面
∴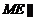 平面
平面 .又
.又 ,
,
∴平面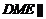 平面
平面 ,又
,又 平面
平面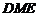
∴ 平面
平面
(Ⅲ)同解法一
19.(本小題滿分12分)某工廠有25周歲以上(含25周歲)工人300名,25周歲以下工人200名.為研究工人的日平均生產量是否與年齡有關.現采用分層抽樣的方法,從中抽取了100名工人,先統計了他們某月的日平均生產件數,然后按工人年齡在“25周歲以上(含25周歲)”和“25周歲以下”分為兩組,在將兩組工人的日平均生產件數分成5組: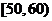 ,
, ,
, ,
, ,
, 分別加以統計,得到如圖所示的頻率分布直方圖.
分別加以統計,得到如圖所示的頻率分布直方圖.
(1)從樣本中日平均生產件數不足60件的工人中隨機抽取2人,求至少抽到一名“25周歲以下組”工人的頻率.
(2)規定日平均生產件數不少于80件者為“生產能手”,請你根據已知條件完成 的列聯表,并判斷是否有
的列聯表,并判斷是否有
的把握認為“生產能手與工人所在的年齡組有關”?


附表:

本小題主要考查古典概型、抽樣方法、獨立性檢驗等基礎知識,考查運算求解能力、應用意識,考查必然和或然思想、化歸與轉化思想等,滿分12分.
解:(Ⅰ)由已知得,樣本中有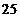 周歲以上組工人
周歲以上組工人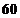 名,
名,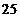 周歲以下組工人
周歲以下組工人 名
名
所以,樣本中日平均生產件數不足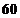 件的工人中,
件的工人中,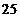 周歲以上組工人有
周歲以上組工人有 (人),
(人),
記為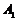 ,
,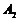 ,
, ;
;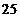 周歲以下組工人有
周歲以下組工人有 (人),記為
(人),記為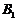 ,
,
從中隨機抽取 名工人,所有可能的結果共有
名工人,所有可能的結果共有 種,他們是:
種,他們是: ,
, ,
,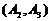 ,
, ,
, ,
, ,
, ,
, ,
, ,
,
其中,至少有名“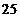 周歲以下組”工人的可能結果共有
周歲以下組”工人的可能結果共有 種,它們是:
種,它們是: ,
, ,
, ,
, ,
, ,
, ,
, .故所求的概率:
.故所求的概率: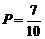
(Ⅱ)由頻率分布直方圖可知,在抽取的 名工人中,“
名工人中,“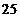 周歲以上組”中的生產能手
周歲以上組”中的生產能手 (人),“
(人),“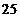 周歲以下組”中的生產能手
周歲以下組”中的生產能手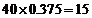 (人),據此可得
(人),據此可得 列聯表如下:
列聯表如下:
生產能手 | 非生產能手 | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
所以得: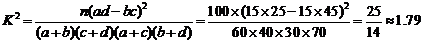
因為 ,所以沒有
,所以沒有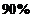 的把握認為“生產能手與工人所在的年齡組有關”
的把握認為“生產能手與工人所在的年齡組有關”