一. 選擇題:本小題共10小題,每小題5分,共50分。在每小題給出的四個選項中,只有一項是符合題目要求的。
1. 函數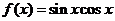 最小值是
最小值是
A.-1 B. 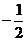 C.
C. 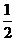 D.1
D.1
1.【答案】:B
[解析]∵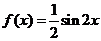 ∴
∴ .故選B
.故選B
2.已知全集U=R,集合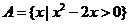 ,則
,則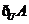 等于
等于
A. { x ∣0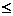 x
x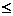 2} B { x ∣0<x<2}
2} B { x ∣0<x<2}
C. { x ∣x<0或x>2} D { x ∣x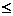 0或x
0或x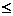 2}
2}
2.【答案】:A
[解析]∵計算可得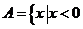 或
或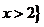 ∴
∴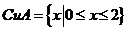 .故選A
.故選A
3.等差數列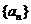 的前n項和為
的前n項和為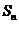 ,且
,且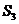 =6,
=6,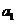 =4, 則公差d等于
=4, 則公差d等于
A.1 B 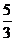 C.- 2 D 3
C.- 2 D 3
3.【答案】:C
[解析]∵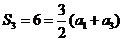 且
且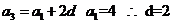 .故選C
.故選C
4. 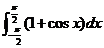 等于
等于
A.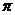 B. 2 C.
B. 2 C. 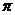 -2 D.
-2 D. 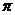 +2
+2
4.【答案】:D
[解析]∵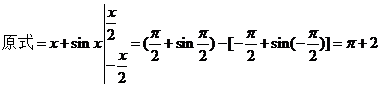 .故選D
.故選D
5.下列函數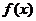 中,滿足“對任意
中,滿足“對任意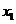 ,
,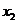
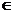 (0,
(0,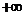 ),當
),當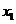 <
<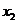 時,都有
時,都有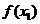 >
>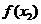 的是
的是
A.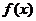 =
= B.
B. 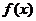 =
=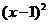 C .
C .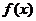 =
=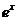 D
D 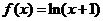
5.【答案】:A
[解析]依題意可得函數應在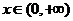 上單調遞減,故由選項可得A正確。
上單調遞減,故由選項可得A正確。
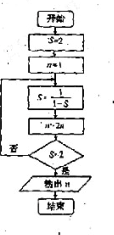
6.閱讀右圖所示的程序框圖,運行相應的程序,輸出的結果是
A.2 B .4 C. 8 D .16
6.【答案】:C
[解析]由算法程序圖可知,在n =4前均執行”否”命令,故n=2×4=8. 故選C
7.設m,n是平面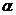 內的兩條不同直線,
內的兩條不同直線,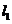 ,
,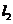 是平面
是平面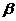 內的兩條相交直線,則
內的兩條相交直線,則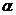 //
// 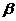 的一個充分而不必要條件是
的一個充分而不必要條件是

A.m // 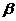 且l //
且l // 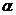 B. m // l 且n // l
B. m // l 且n // l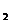
C. m // 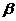 且n //
且n // 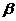 D. m //
D. m // 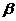 且n // l
且n // l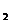
7.【答案】:B
[解析]若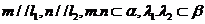 ,則可得
,則可得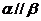 .若
.若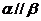 則存在
則存在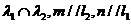
8.已知某運動員每次投籃命中的概率都為40%。現采用隨機模擬的方法估計該運動
員三次投籃恰有兩次命中的概率:先由計算器算出0到9之間取整數值的隨機數,
指定1,2,3,4表示命中,5,6,,7,8,9,0表示不命中;再以每三個隨機數為一組,代表三次投籃的結果。經隨機模擬產生了20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為
A.0.35 B 0.25 C 0.20 D 0.15
8.【答案】:B
[解析]由隨機數可估算出每次投籃命中的概率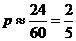 則三次投籃命中兩次為
則三次投籃命中兩次為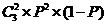
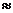 0.25故選B
0.25故選B
9.設a,b,c為同一平面內具有相同起點的任意三個非零向量,且滿足a與b不共線,
a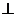 c ∣a∣=∣c∣,則∣b • c∣的值一定等于
c ∣a∣=∣c∣,則∣b • c∣的值一定等于

A. 以a,b為兩邊的三角形面積 B 以b,c為兩邊的三角形面積
C.以a,b為鄰邊的平行四邊形的面積 D 以b,c為鄰邊的平行四邊形的面積
9.【答案】:C
[解析]依題意可得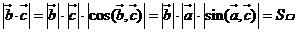 故選C.
故選C.
10.函數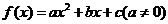 的圖象關于直線
的圖象關于直線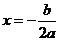 對稱。據此可推測,對任意的非零實數a,b,c,m,n,p,關于x的方程
對稱。據此可推測,對任意的非零實數a,b,c,m,n,p,關于x的方程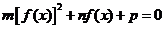 的解集都不可能是
的解集都不可能是
A. 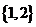 B
B 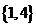 C
C 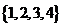 D
D 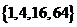
10. 【答案】:D
[解析]本題用特例法解決簡潔快速,對方程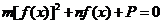 中
中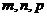 分別賦值求出
分別賦值求出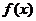 代入
代入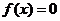 求出檢驗即得.
求出檢驗即得.