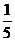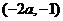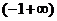21.本小題主要考查函數、導數等基礎知識,考查推理論證能力、運算求解能力、考查函數與方程思想、數形結合思想、化歸與轉化思想、分類與整合思想,滿分12分。
解法一:
(I)依題意,得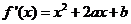
由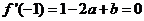 得
得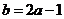
(Ⅱ)由(I)得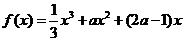 (
(
故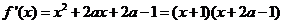
令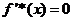 ,則
,則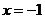 或
或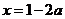
①當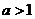 時,
時,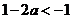
當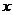 變化時,
變化時,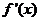 與
與 的變化情況如下表:
的變化情況如下表:
|
|
|
|
| + | — | + |
| 單調遞增 | 單調遞減 | 單調遞增 |
由此得,函數 的單調增區間為
的單調增區間為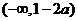 和
和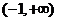 ,單調減區間為
,單調減區間為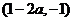
②由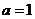 時,
時,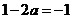 ,此時,
,此時,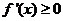 恒成立,且僅在
恒成立,且僅在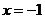 處
處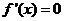 ,故函數
,故函數 的單調區間為R
的單調區間為R
③當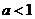 時,
時,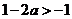 ,同理可得函數
,同理可得函數 的單調增區間為
的單調增區間為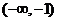 和
和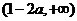 ,單調減區間為
,單調減區間為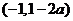
綜上:
當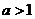 時,函數
時,函數 的單調增區間為
的單調增區間為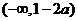 和
和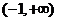 ,單調減區間為
,單調減區間為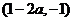 ;
;
當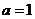 時,函數
時,函數 的單調增區間為R;
的單調增區間為R;
當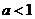 時,函數
時,函數 的單調增區間為
的單調增區間為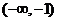 和
和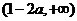 ,單調減區間為
,單調減區間為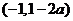
(Ⅲ)當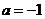 時,得
時,得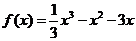
由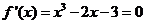 ,得
,得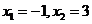
由(Ⅱ)得 的單調增區間為
的單調增區間為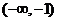 和
和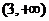 ,單調減區間為
,單調減區間為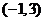
所以函數 在
在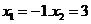 處取得極值。
處取得極值。
故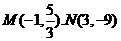
所以直線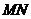 的方程為
的方程為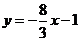
由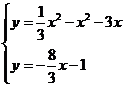 得
得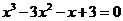
令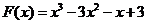
易得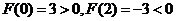 ,而
,而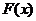 的圖像在
的圖像在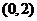 內是一條連續不斷的曲線,
內是一條連續不斷的曲線,
故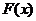 在
在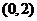 內存在零點
內存在零點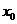 ,這表明線段
,這表明線段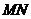 與曲線
與曲線 有異于
有異于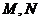 的公共點
的公共點
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)當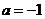 時,得
時,得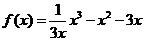 ,由
,由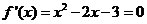 ,得
,得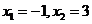
由(Ⅱ)得 的單調增區間為
的單調增區間為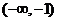 和
和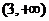 ,單調減區間為
,單調減區間為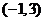 ,所以函數
,所以函數 在
在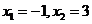 處取得極值,
處取得極值,
故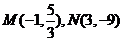
所以直線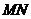 的方程為
的方程為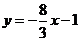
由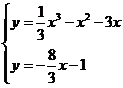 得
得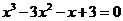
解得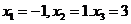
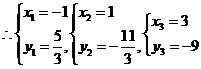
所以線段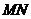 與曲線
與曲線 有異于
有異于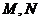 的公共點
的公共點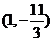
22.本小題主要考查直線、橢圓、直線與圓錐曲線的位置關系等基礎知識,考查推理論證能力、運算求解能力,考查數形結合思想、化歸與轉化思想,滿分14分
解法一:
(I)由已知得,橢圓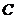 的左頂點為
的左頂點為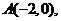 上頂點為
上頂點為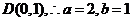
故橢圓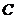 的方程為
的方程為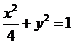
(Ⅱ)直線AS的斜率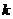 顯然存在,且
顯然存在,且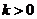 ,故可設直線
,故可設直線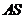 的方程為
的方程為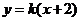 ,從而
,從而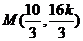
由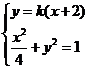 得
得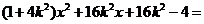 0
0
設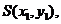 則
則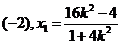 得
得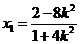 ,從而
,從而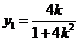
即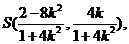 又
又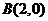
由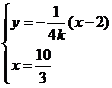 得
得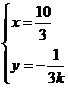
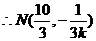
故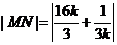
又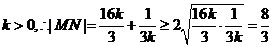
當且僅當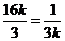 ,即
,即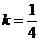 時等號成立
時等號成立
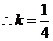 時,線段
時,線段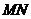 的長度取最小值
的長度取最小值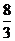
(Ⅲ)由(Ⅱ)可知,當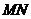 取最小值時,
取最小值時,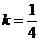
此時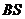 的方程為
的方程為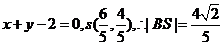
要使橢圓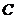 上存在點
上存在點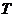 ,使得
,使得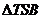 的面積等于
的面積等于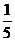 ,只須
,只須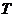 到直線
到直線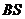 的距離等于
的距離等于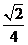 ,所以
,所以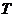 在平行于
在平行于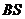 且與
且與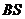 距離等于
距離等于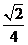 的直線
的直線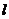 上。
上。
設直線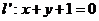
則由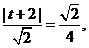 解得
解得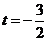 或
或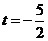
① 當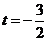 由
由 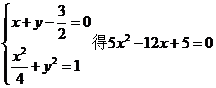
由于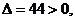 故直線
故直線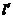 與橢圓C有兩個不同的交點
與橢圓C有兩個不同的交點
② 當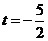 由
由 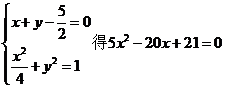
由于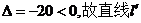 與橢圓C沒有交點
與橢圓C沒有交點
綜上所述,當線段MN的長度最小時,橢圓上僅存在兩個不同的點T,使得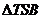 的面積等于
的面積等于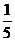
解法二:
(Ⅰ)同解法一
(Ⅱ)設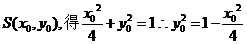
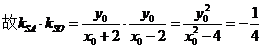
設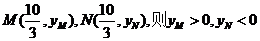
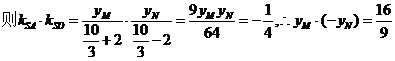
故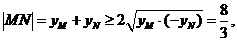
當且僅當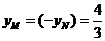 時等號成立
時等號成立
即M,N的長度的最小值為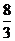
(Ⅲ)由(Ⅱ)知,當M,N取最小值時,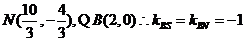
此時BS的方程為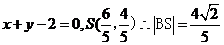
設與直線BS平行的直線方程為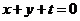
由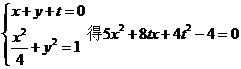
當直線與橢圓C有唯一公共點時,有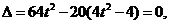 解得
解得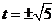
當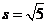 時,兩平行直線BS:
時,兩平行直線BS: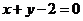 與
與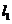 :
: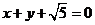 間的距離
間的距離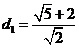 ,
,
當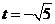 時,兩平行直線BS:
時,兩平行直線BS: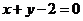 與
與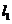 :
: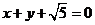 間的距離
間的距離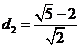 ,
,
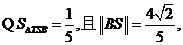 故
故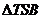 在BS邊上的高
在BS邊上的高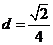
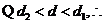 橢圓C上存在兩個不同的點T,使得
橢圓C上存在兩個不同的點T,使得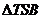 的面積等于
的面積等于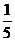
即線段MN的長度最小時,橢圓C上僅存在兩個不同的點T,使得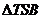 的面積等于
的面積等于