(19)(本小題滿分12分)
如圖,已知兩個(gè)正方形ABCD 和DCEF不在同一平面內(nèi),M,N分別為AB,DF的中點(diǎn)。
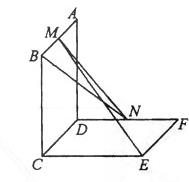
(I)若CD=2,平面ABCD ⊥平面DCEF,求直線MN的長;
(II)用反證法證明:直線ME 與 BN 是兩條異面直線。
(19)解
(Ⅰ)取CD的中點(diǎn)G連結(jié)MG,NG.
因?yàn)锳BCD,DCEF為正方形,且邊長為2,
所以MG⊥CD,MG=2,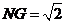 .
.
因?yàn)槠矫鍭BCD⊥平面DCEF,
所以MG⊥平面DCEF,可得MG⊥NG.
所以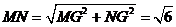 ……6分
……6分
(Ⅱ)假設(shè)直線ME與BN共面, …..8分
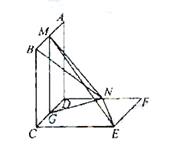
則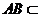 平面MBEN,且平面MBEN與平面DCEF交于EN,
平面MBEN,且平面MBEN與平面DCEF交于EN,
由已知,兩正方形不共面,故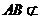 平面DCEF.
平面DCEF.
又AB∥CD,所以AB∥平面DCEF.而EN為平面MBEN與平面DCEF的交線,
所以AB∥EN.
又AB∥CD∥EF,
所以EN∥EF,這與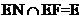 矛盾,故假設(shè)不成立。
矛盾,故假設(shè)不成立。
所以ME與BN不共面,它們是異面直線。 ……..12分
(20)(本小題滿分12分)
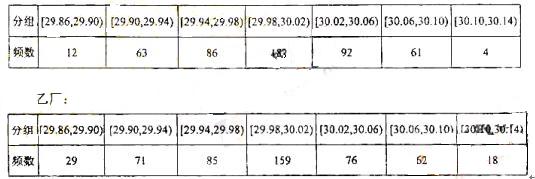
某企業(yè)有兩個(gè)分廠生產(chǎn)某種零件,按規(guī)定內(nèi)徑尺寸(單位:mm)的值落在(29.94,30.06)的零件為優(yōu)質(zhì)品。從兩個(gè)分廠生產(chǎn)的零件中個(gè)抽出500件,量其內(nèi)徑尺寸,的結(jié)果如下表:
甲廠
(1)試分別估計(jì)兩個(gè)分廠生產(chǎn)的零件的優(yōu)質(zhì)品率;
(2)由于以上統(tǒng)計(jì)數(shù)據(jù)填下面 列聯(lián)表,并問是否有99%的把握認(rèn)為“兩個(gè)分廠生產(chǎn)的零件的質(zhì)量有差異”。
列聯(lián)表,并問是否有99%的把握認(rèn)為“兩個(gè)分廠生產(chǎn)的零件的質(zhì)量有差異”。
甲 廠 | 乙 廠 | 合計(jì) | |
優(yōu)質(zhì)品 | |||
非優(yōu)質(zhì)品 | |||
合計(jì) |
附: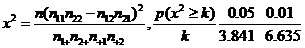

(20)解:
(Ⅰ)甲廠抽查的產(chǎn)品中有360件優(yōu)質(zhì)品,從而甲廠生產(chǎn)的零件的優(yōu)質(zhì)品率估計(jì)為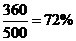 ; ……6分
; ……6分
乙廠抽查的產(chǎn)品中有320件優(yōu)質(zhì)品,從而乙廠生產(chǎn)的零件的優(yōu)質(zhì)品率估計(jì)為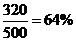
(Ⅱ)
甲廠 | 乙廠 | 合計(jì) | |
優(yōu)質(zhì)品 | 360 | 320 | 680 |
非優(yōu)質(zhì)品 | 140 | 180 | 320 |
合計(jì) | 500 | 500 | 1000 |
……8分
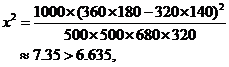

所以有99%的把握認(rèn)為“兩個(gè)分廠生產(chǎn)的零件的質(zhì)量有差異”。 ……12分
(21)(本小題滿分12分)
設(shè)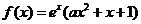 ,且曲線y=f(x)在x=1處的切線與x軸平行。
,且曲線y=f(x)在x=1處的切線與x軸平行。
(I)求a的值,并討論f(x)的單調(diào)性;
(II)證明:當(dāng)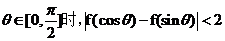

(21)解:
(Ⅰ)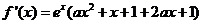 .有條件知,
.有條件知,
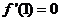 ,故
,故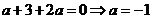 . ………2分
. ………2分
于是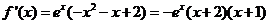 .
.
故當(dāng)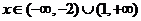 時(shí),
時(shí),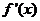 <0;
<0; 
當(dāng)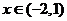 時(shí),
時(shí),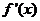 >0.
>0.
從而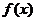 在
在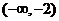 ,
,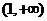 單調(diào)減少,在
單調(diào)減少,在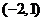 單調(diào)增加. ………6分
單調(diào)增加. ………6分
(Ⅱ)由(Ⅰ)知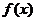 在
在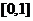 單調(diào)增加,故
單調(diào)增加,故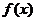 在
在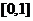 的最大值為
的最大值為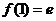 ,
,
最小值為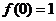 .
. 
從而對任意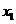 ,
,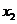
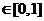 ,有
,有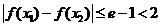 . ………10分
. ………10分
而當(dāng)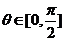 時(shí),
時(shí),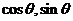
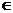
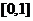 .
.
從而 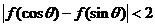 ………12分
………12分
(22)(本小題滿分12分)
已知,橢圓C以過點(diǎn)A(1,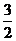 ),兩個(gè)焦點(diǎn)為(-1,0)(1,0)。
),兩個(gè)焦點(diǎn)為(-1,0)(1,0)。
(1) 求橢圓C的方程;
(2) E,F是橢圓C上的兩個(gè)動點(diǎn),如果直線AE的斜率與AF的斜率互為相反數(shù),證明直線EF的斜率為定值,并求出這個(gè)定值。
(22)解:(Ⅰ)由題意,c=1,可設(shè)橢圓方程為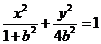 。
。
因?yàn)锳在橢圓上,所以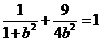 ,解得
,解得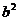 =3,
=3,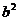 =
=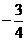 (舍去)。
(舍去)。
所以橢圓方程為 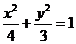 . ......4分
. ......4分
(Ⅱ)設(shè)直線AE方程:得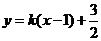 ,代入
,代入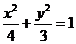 得
得
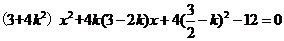
設(shè)E(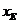 ,
,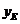 ),F(
),F(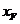 ,
,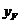 ).因?yàn)辄c(diǎn)A(1,
).因?yàn)辄c(diǎn)A(1,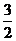 )在橢圓上,所以
)在橢圓上,所以
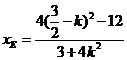 ,
,
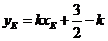 。 .......8分
。 .......8分
又直線AF的斜率與AE的斜率互為相反數(shù),在上式中以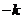 代
代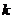 ,可得
,可得
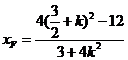 ,
,
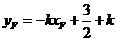 。
。
所以直線EF的斜率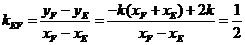 。
。
即直線EF的斜率為定值,其值為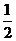 。 .......12分
。 .......12分