第Ⅰ卷
一、選擇題:本大題共12小題,每小題5分,在每小題給出的四個選項中,只有一項是符合題目要求的.
(1) a為正實數,i為虛數單位,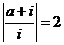 ,則a=( )
,則a=( )
(A)2 (B)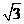 (C)
(C)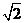 (D)1
(D)1

(3)已知F是拋物線y2=x的焦點,A,B是該拋物線上的兩點,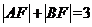 ,則線段AB的中點到y軸的距離為( )
,則線段AB的中點到y軸的距離為( )
(A)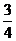 (B) 1 (C)
(B) 1 (C)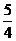 (D)
(D)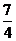
答案: C
解析:設A、B的橫坐標分別是m、n,由拋物線定義,得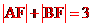 =m+
=m+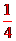 +n+
+n+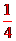 = m+n+
= m+n+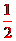 =3,故m+n=
=3,故m+n=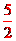 ,
,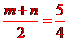 ,故線段AB的中點到y軸的距離為
,故線段AB的中點到y軸的距離為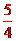 .
.
(4)△ABC的三個內角A、B、C所對的邊分別為a,b,c,asin AsinB+bcos2A=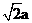 則
則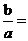 ( )
( )
(A) 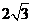 (B)
(B) 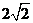 (C)
(C) 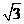 (D)
(D)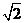

(6)執行右面的程序框圖,如果輸入的n是4,則輸出的P是
(A) 8 (B) 5 (C) 3 (D) 2
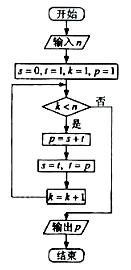
答案:C
解析:第一次執行結果:p=1,s=1,t=1,k=2;
第二次執行結果:p=2,s=1,t=2,k=3;
第三次執行結果:p=3,s=2,t=3,k=4;結束循環,輸出p的值4.
(7)設sin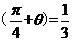 ,則
,則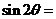 ( )
( )
(A) 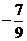 (B)
(B) 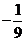 (C)
(C) 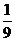 (D)
(D)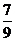
答案: A
解析: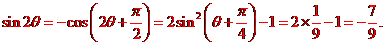
(8)如圖,四棱錐S-ABCD的底面為正方形,SD⊥底面ABCD,則下列結論中不正確的是( )
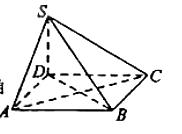
(A) AC⊥SB
(B) AB∥平面SCD
(C) SA與平面SBD所成的角等于SC與平面SBD所成的角
(D)AB與SC所成的角等于DC與SA所成的角
答案: D
解析:對于A:因為SD⊥平面ABCD,所以DS⊥AC.
因為四邊形ABCD為正方形,所以AC⊥BD,故AC⊥平面ABD,因為SB 平面ABD,所以AC⊥SB,正確.
平面ABD,所以AC⊥SB,正確.
對于B:因為AB//CD,所以AB//平面SCD.
對于C:設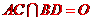 .因為AC⊥平面ABD,所以SA和SC在平面SBD內的射影為SO,則∠ASO和∠CSO就是SA與
.因為AC⊥平面ABD,所以SA和SC在平面SBD內的射影為SO,則∠ASO和∠CSO就是SA與 平面SBD所成的角和SC與平面SBD所成的角,二者相等,正確.故選D.
平面SBD所成的角和SC與平面SBD所成的角,二者相等,正確.故選D.
(9)設函數f(x)=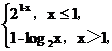 則滿足f(x)≤2的x的取值范圍是( )
則滿足f(x)≤2的x的取值范圍是( )
(A)[-1,2] (B)[0,2] (C)[1,+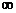 ) (D)[0,+
) (D)[0,+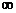 )
)

(11)函數f(x)的定義域為R,f(-1)=2,對任意x∈R,f’(x)>2,則f(x)>2x+4的解集為( )
(A)(-1,1) (B)(-1,+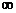 ) (C)(-
) (C)(-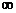 ,-1) (D)(-
,-1) (D)(-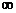 ,+
,+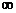 )
)
答案: B
解析:設g(x)= f(x)-(2x+4), g’(x)= f’(x)-2.因為對任意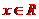 ,f’(
,f’( x)>2,所以對任意
x)>2,所以對任意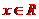 ,g’(x)>0,則函數g(x)在R上單調遞增.又因為g(-1)= f(-1)-(-2+4)=0,故g(x)>0,即f(x)>2x+4的解集為(-1,+
,g’(x)>0,則函數g(x)在R上單調遞增.又因為g(-1)= f(-1)-(-2+4)=0,故g(x)>0,即f(x)>2x+4的解集為(-1,+ ).
).
(12)已知球的直徑SC=4,A,B是該球球面上的兩點,AB=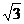 ,
,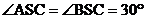 ,則棱錐S-ABC的體積為( )
,則棱錐S-ABC的體積為( )
(A)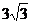 (B)
(B)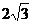 (C)
(C)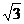
 (D)1
(D)1