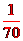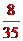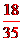第Ⅱ卷
本卷包括必考題和選考題兩部分.第13題-第21題為必考題,每個(gè)試題考生都必須做答.第22題-第24題為選考題,考生根據(jù)要求做答.
二、填空題 :本大題共4小題,
:本大題共4小題, 每小題5分.
每小題5分.
(13)已知點(diǎn)(2,3)在雙曲線C: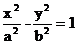 (a>0,b>0)上,C的焦距為4,則它的離心率為_____________.
(a>0,b>0)上,C的焦距為4,則它的離心率為_____________.
答案: 2
解析:由題意得,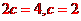 ,
,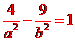 ,
,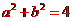 ,解得a=1,故離心率為2.
,解得a=1,故離心率為2.
(14) 調(diào)查了某地若干戶家庭的年收入x(單位:萬元)和年飲食支 出y(單位:萬元),調(diào)查顯示年收入x與年飲食支出y具有線性相關(guān)關(guān)系,并由調(diào)查數(shù)據(jù)得到y(tǒng)對x的回歸直線方程:
出y(單位:萬元),調(diào)查顯示年收入x與年飲食支出y具有線性相關(guān)關(guān)系,并由調(diào)查數(shù)據(jù)得到y(tǒng)對x的回歸直線方程: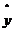 =0.254x+0.321.由回歸直線方程可知,家庭年收入每增加1萬元,年飲食支出平均增加_______萬元.
=0.254x+0.321.由回歸直線方程可知,家庭年收入每增加1萬元,年飲食支出平均增加_______萬元.

(16)已知函數(shù)f(x)=Atan(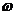 x+
x+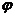 )(
)(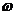 >0,
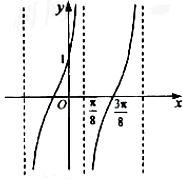
>0,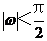 ),y=f(x)的部分圖像如下圖,則f(
),y=f(x)的部分圖像如下圖,則f(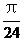 )=____________.
)=____________.
答案: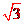
解析:函數(shù)f(x)的周期是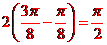 ,故
,故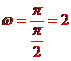 ,由
,由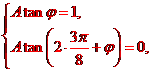 得
得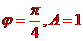 .所以
.所以 ,故
,故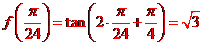 .
.
三、解答題:解答應(yīng)寫文字說明,證明過程或演算步驟.
(17)(本小題滿分12分)
已知等差數(shù)列{an}滿足a2=0,a6+a8= -10
(I)求數(shù)列{an}的通項(xiàng)公式;
(II )求數(shù)列
)求數(shù)列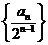 的前n項(xiàng)和.
的前n項(xiàng)和.

(18)(本小題滿分12分)
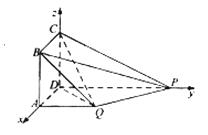
如圖,四邊形ABCD為正方形,PD⊥平面ABCD,PD∥QA,QA=AB=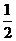 PD.
PD.

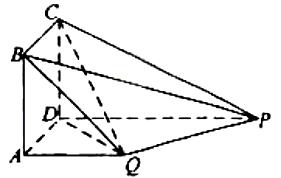
(I)證明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.

即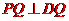 ,
,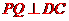 .故
.故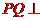 平面DCQ,
平面DCQ,
又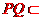 平面PQC,所以平面PQC
平面PQC,所以平面PQC 平面DCQ.
平面DCQ.
(II)依題意得B(1,0,1),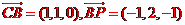 ,
,
設(shè)n=(x,y,z)是平面PBC的法向量,則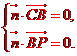 即
即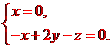
因此,取n=(0,-1,-2).
設(shè)m是平面PBQ的法向量,則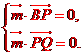
可取m=(1,1,1),所以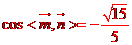 ,
,
故二面角Q-BP-C的余弦值為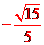 .
.
19.(本小題滿分12分)
某農(nóng)場計(jì)劃種植某種新作物,為此對這種作物的兩個(gè)品種(分別稱為品種甲和品種乙)進(jìn)行田間試驗(yàn).選取兩大塊地,每大塊地分成n小塊地,在總共2n小塊地中,隨機(jī)選n小塊地種植品種甲,另外n小塊地種植品種乙.
(I)假設(shè)n=4,在第一大塊地中,種植品種甲的小塊地的數(shù)目記為X,求X的分布列和數(shù)學(xué)期望;
(II)試驗(yàn)時(shí)每大塊地分成8小塊,即n=8,試驗(yàn)結(jié)束后得到品種甲和品種乙在個(gè)小塊地上的每公頃產(chǎn)量(單位:kg/hm2)如下表:

分別求品種甲和品種乙的每公頃產(chǎn)量的樣本平均數(shù)和樣本方差;根據(jù)試驗(yàn)結(jié)果,你認(rèn)為應(yīng)該種植哪一品種?
附:樣本數(shù)據(jù)x1,x2,…,xa的樣本方差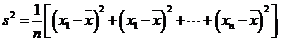 ,其中
,其中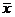 為樣本平均數(shù).
為樣本平均數(shù).
解析:(I)X可能的取值為0,1,2,3,4,且
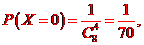
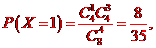
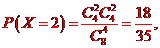
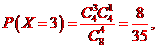
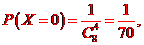
即X的分布列為
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
X的數(shù)學(xué)期望是:
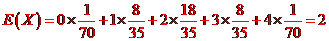 .
.
(II)品種甲的每公頃產(chǎn)量的樣本平均數(shù)和樣本方差分別是:
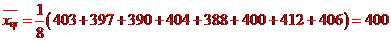 ,
,
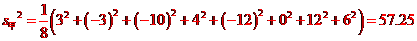 .
.
品種乙的每公頃產(chǎn)量的樣本平均數(shù)和樣本方差分別是:
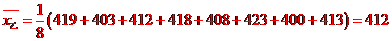 ,
,
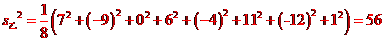 ,
,
由以上結(jié)果可以看出 ,品種乙的樣本平均數(shù)大于品種甲的樣本平均數(shù),且兩品種的樣本方差差異不大,故應(yīng)該選擇種植品種乙.
,品種乙的樣本平均數(shù)大于品種甲的樣本平均數(shù),且兩品種的樣本方差差異不大,故應(yīng)該選擇種植品種乙.