(20)(本小題滿分12分)
如圖,已知橢圓C1的中心在原點O,長軸左、右端點M,N在x軸上,橢圓C2的短軸為MN,且C1,C2的離心率都為e,直線l⊥MN,l與C1交于兩點,與C2交于兩點,這四點按縱坐標從大到小依次為A,B,C,D.
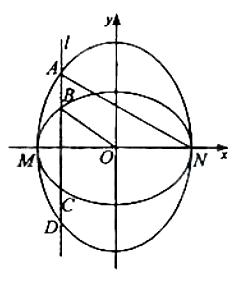
(I)設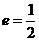 ,求
,求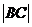 與
與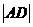 的比值;
的比值;
(II)當e變化時,是否存在直線l,使得BO∥AN,并說明理由
解析:(I)因為C1,C2的離心率相同,故依題意可設
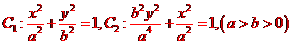 .
.
設直線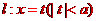 分別和C
分別和C 1,C2聯立,求得
1,C2聯立,求得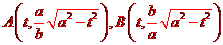 .
.
當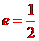 時,
時,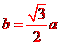 ,分別用yA,yB表示A、B的縱坐標,可知
,分別用yA,yB表示A、B的縱坐標,可知
|BC|:AD|=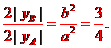
(II)t=0時的l不符合題意,t≠0時,BO//AN當且僅當BO的斜率kBO與AN的斜率kAN相等,即
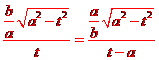 ,
,
解得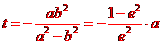 .
.
因為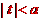 ,又
,又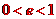 ,所以
,所以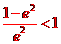 ,解得
,解得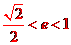 .
.
所以當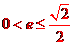 時,不存在直線l,使得BO//AN;當
時,不存在直線l,使得BO//AN;當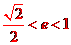 時,存在直線l使得BO//AN.
時,存在直線l使得BO//AN.
(21)(本小題滿分12分)
已知函數f(x)=lnx-ax2+(2-a)x.
(I)討論f(x)的單調性;
(II)設a>0,證明:當0<x<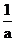 時,f(
時,f(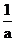 +x)>f(
+x)>f(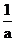 -x);
-x);
(III)若函數y=f(x)的圖像與x軸交于A,B兩點,線段AB中點的橫坐標為x0,證明:f’( x0)<0.
解析:(I)f(x)的定義域為(0,+∞),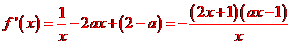 ,
,
①若a≤0,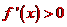 ,所以f(x)在(0,+∞)單調增加;
,所以f(x)在(0,+∞)單調增加;
②若a>0,則由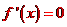 得
得
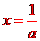 ,且當
,且當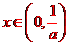 時,
時,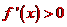 ,當
,當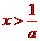 時,
時,
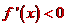 ,所以f(x)在
,所以f(x)在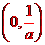 單調增加,在
單調增加,在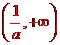 單調
單調 減少.
減少.
(II)設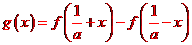 ,則
,則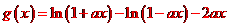 ,
,
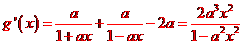 ,
,
當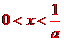 時,
時,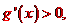 而
而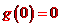 ,所以
,所以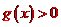 .
.
故當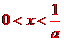 時,
時, 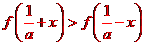

請考生在第22、23、24三題中任選一題做答,如果多做,則按所做的第一題計分.做答是用2B鉛筆在答題卡上把所選題目對應題號下方的方框涂黑.
(22)(本小題滿分10分)選修4-1:幾何證明選講
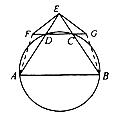
如圖,A,B,C,D四點在同一圓上,AD的延長線與BC的延長線交于E點,且EC=ED.
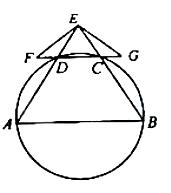
(I)證明:CD//AB;
(II)延長CD到F,延長DC到G,使得EF=EG,證明:A,B,G,F四點共圓.

(23)(本小題滿分10分)選修4-4:坐標系統與參數方程
在平面直角坐標系xOy中,曲線C1的參數方程為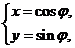 (
(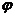 為參數)曲線C2的參數方程為
為參數)曲線C2的參數方程為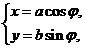 (
(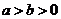 ,
,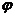 為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=
為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=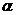 與C1,C2各有一個交點.當
與C1,C2各有一個交點.當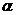 =0時,這兩個交點間的距離為2,當
=0時,這兩個交點間的距離為2,當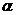 =
=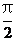 時,這兩個交點重合.
時,這兩個交點重合.
(I)分別說明C1,C2是什么曲線,并求出a與b的值;
(II)設當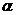 =
=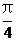 時,l與C1,C2的交點分別為A1,B1,當
時,l與C1,C2的交點分別為A1,B1,當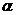 =-
=-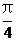 時,l與C1,
時,l與C1,
C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
解析:(I)C1為圓,C2為橢圓.
當 =0時,射線l與C1,C2交點的直角坐標分別是(1,0),(a,0),因為這兩點間的距離為2,所以a=3.
=0時,射線l與C1,C2交點的直角坐標分別是(1,0),(a,0),因為這兩點間的距離為2,所以a=3.
當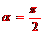 時,射線l與C1,C2交點的直角坐標分別是(0,1),(
時,射線l與C1,C2交點的直角坐標分別是(0,1),( 0,b),因為這兩點重合,所以b=1.
0,b),因為這兩點重合,所以b=1.
(II)C1,C2的普通方程分別為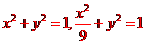 ,
,
當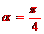 時,射線l與C1交點A1的橫坐標是
時,射線l與C1交點A1的橫坐標是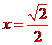 ,與C2交點B1的橫坐標是
,與C2交點B1的橫坐標是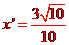 ;
;
當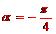 時,射線l與C1 、C2的兩個交點A2 、B2的分別與A1、B1 關于x軸對稱,因此,四邊形與A1 A2B2B1 為梯形.
時,射線l與C1 、C2的兩個交點A2 、B2的分別與A1、B1 關于x軸對稱,因此,四邊形與A1 A2B2B1 為梯形.
故四邊形與A1 A2B2B1 的面積為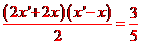 .
.
(24)(本小題滿分10分)選修4-5:不等式選講
已知函數f(x)=|x-2|-|x-5|.
(I)證明:-3≤f(x)≤3;
(II)求不等式f(x)≥x2-8x+15的解集.












