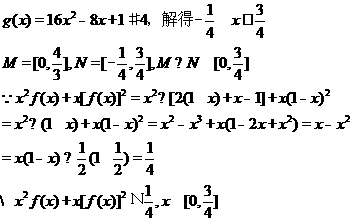第Ⅰ卷(共60分)
一、選擇題:本大題共12個小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項
是符合題目要求的.
1.已知全集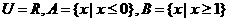 ,則集合
,則集合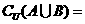 ( )
( )
A.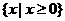 B.
B.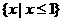 C.
C.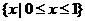 D.
D.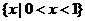
【答案】D
【解析】
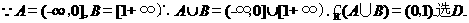
2.設復數z滿足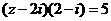 ,則
,則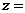 ( )
( )
A.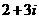 B.
B.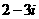 C.
C.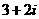 D.
D.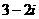
【答案】A
【解析】
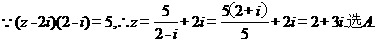
3.已知 ,
,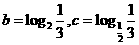 ,則( )
,則( )
A.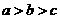 B.
B.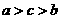 C.
C.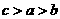 D.
D.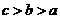
【答案】C
【解析】
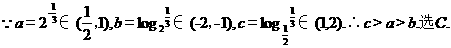
4.已知m,n表示兩條不同直線,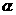 表示平面,下列說法正確的是( )
表示平面,下列說法正確的是( )
A.若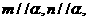 則
則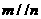 B.若
B.若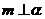 ,
,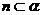 ,則
,則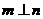
C.若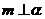 ,
,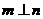 ,則
,則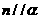 D.若
D.若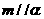 ,
,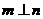 ,則
,則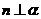
【答案】B
【解析】

5.設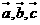 是非零向量,已知命題P:若
是非零向量,已知命題P:若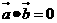 ,
,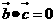 ,則
,則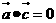 ;命題q:若
;命題q:若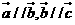 ,則
,則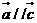 ,則下列命題中真命題是( )
,則下列命題中真命題是( )
A.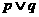 B.
B.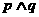 C.
C.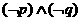 D.
D.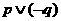
【答案】A
【解析】
命題p為假,命題q為真,所以A正確。選A
6把椅子擺成一排,3人隨機就座,任何兩人不相鄰的做法種數為( )
A.144 B.120 C.72 D.24
【答案】D
【解析】
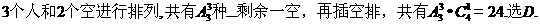
7.某幾何體三視圖如圖所示,則該幾何體的體積為( )
A.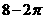 B.
B.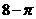 C.
C.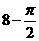 D.
D.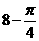
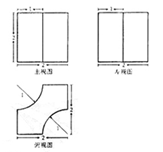
【答案】B
【解析】
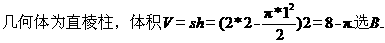
8.設等差數列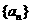 的公差為d,若數列
的公差為d,若數列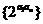 為遞減數列,則( )
為遞減數列,則( )
A.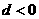 B.
B.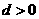 C.
C.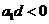 D.
D.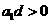
【答案】C
【解析】

9.將函數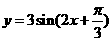 的圖象向右平移
的圖象向右平移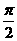 個單位長度,所得圖象對應的函數( )
個單位長度,所得圖象對應的函數( )
A.在區間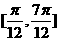 上單調遞減
上單調遞減
B.在區間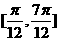 上單調遞增
上單調遞增
C.在區間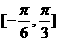 上單調遞減
上單調遞減
D.在區間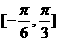 上單調遞增
上單調遞增
【答案】B
【解析】

10.已知點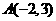 在拋物線C:
在拋物線C: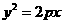 的準線上,過點A的直線與C在第一象限相切于點B,記C的焦點為F,則直線BF的斜率為( )
的準線上,過點A的直線與C在第一象限相切于點B,記C的焦點為F,則直線BF的斜率為( )
A.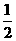 B.
B.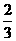 C.
C.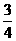 D.
D.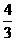
【答案】D
【解析】

11.當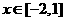 時,不等式
時,不等式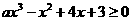 恒成立,則實數a的取值范圍是( )
恒成立,則實數a的取值范圍是( )
A.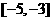 B.
B.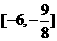 C.
C.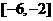 D.
D.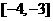
【答案】C
【解析】

12.已知定義在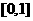 上的函數
上的函數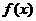 滿足:
滿足:
①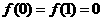 ;
;
②對所有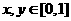 ,且
,且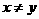 ,有
,有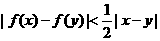 .
.
若對所有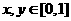 ,
,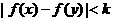 ,則k的最小值為( )
,則k的最小值為( )
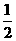 B.
B.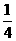 C.
C.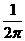 D.
D.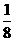
【答案】B
【解析】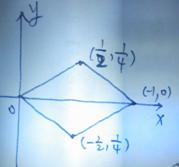

第Ⅱ卷(共90分)
二、填空題(每題5分,滿分20分,將答案填在答題紙上)
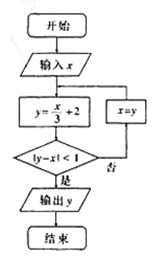
13.執行右側的程序框圖,若輸入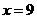 ,則輸出
,則輸出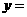 ____________ .
____________ .
【答案】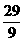
【解析】
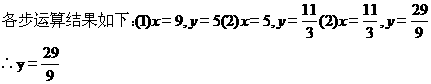
14.正方形的四個頂點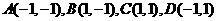 分別在拋物線
分別在拋物線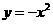 和
和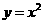 上,如圖所示,若將一個質點隨機投入正方形ABCD中,則質點落在陰影區域的概率是_________.
上,如圖所示,若將一個質點隨機投入正方形ABCD中,則質點落在陰影區域的概率是_________.
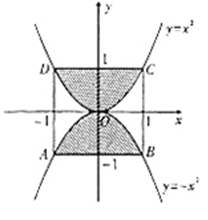
【答案】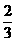
【解析】
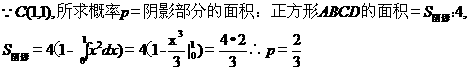
15.已知橢圓C: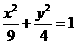 ,點M與C的焦點不重合,若M關于C的焦點的對稱點分別為A,B,線段MN的中點在C上,則
,點M與C的焦點不重合,若M關于C的焦點的對稱點分別為A,B,線段MN的中點在C上,則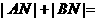 _________ .
_________ .
【答案】12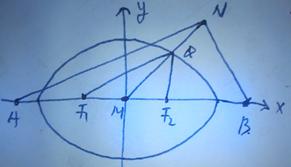
【解析】
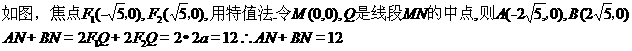
16.對于 ,當非零實數a,b滿足
,當非零實數a,b滿足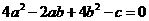 ,且使
,且使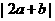 最大時,
最大時,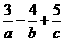 的最小值為 _________ .
的最小值為 _________ .
【答案】-2
【解析】

三、解答題 (本大題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.)
17.(本小題滿分12分)
在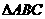 中,內角A,B,C的對邊a,b,c,且
中,內角A,B,C的對邊a,b,c,且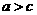 ,已知
,已知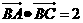 ,
,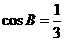 ,
,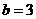 ,求:
,求:
(1)a和c的值;
(2)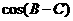 的值.
的值.
【答案】 (1) 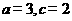 (2)
(2) 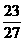
【解析】
(1)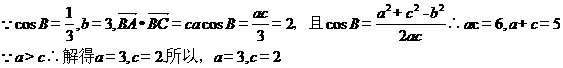
(2)
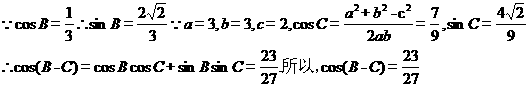
18. (本小題滿分12分)
一家面包房根據以往某種面包的銷售記錄,繪制了日銷售量的頻率分布直方圖,如圖所示:
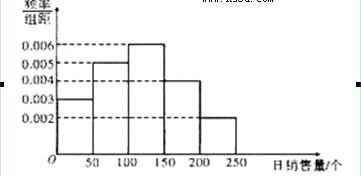
將日銷售量落入各組的頻率視為概率,并假設每天的銷售量相互獨立.
(1)求在未來連續3天里,有連續2天的日銷售量都不低于100個且另一天的日銷售量低于50個的概率;
(2)用X表示在未來3天里日銷售量不低于100個的天數,求隨機變量X的分布列,期望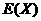 及方差
及方差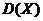 .
.
【答案】 (1) 0.108 (2) 1.8,0.72
【解析】
(1)

(2)
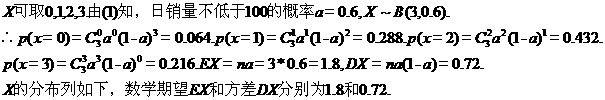
X | 0 | 1 | 2 | 3 |
P | 0.064 | 0.288 | 0.432 | 0.216 |
19. (本小題滿分12分)
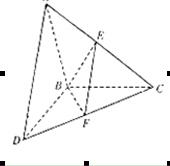
如圖, 和
和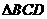 所在平面互相垂直,且
所在平面互相垂直,且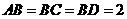 ,
,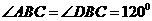 ,E、F分別為AC、DC的中點.
,E、F分別為AC、DC的中點.
(1)求證: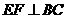 ;
;
(2)求二面角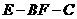 的正弦值.
的正弦值.
【答案】 (1) 省略(2) 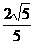
【解析】
(1)

(2)

20. (本小題滿分12分)
圓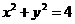 的切線與x軸正半軸,y軸正半軸圍成一個三角形,當該三角形面積最小時,切點為P(如圖),雙曲線
的切線與x軸正半軸,y軸正半軸圍成一個三角形,當該三角形面積最小時,切點為P(如圖),雙曲線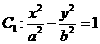 過點P且離心率為
過點P且離心率為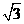 .
.
(1)求 的方程;
的方程;
(2)橢圓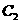 過點P且與
過點P且與 有相同的焦點,直線
有相同的焦點,直線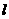 過
過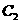 的右焦點且與
的右焦點且與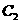 交于A,B兩點,若以線段AB為直徑的圓心過點P,求
交于A,B兩點,若以線段AB為直徑的圓心過點P,求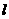 的方程
的方程
【答案】 (1) 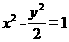 (2)
(2) 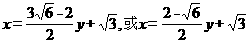
【解析】
(1)

(2)
.
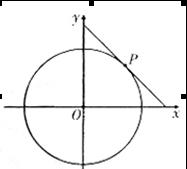
21. (本小題滿分12分)
已知函數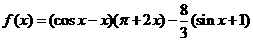 ,
,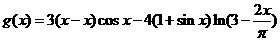 .
.
證明:(1)存在唯一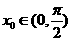 ,使
,使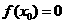 ;
;
存在唯一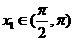 ,使
,使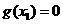 ,且對(1)中的
,且對(1)中的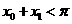 .
.
【答案】 (1) 0.108 (2) 1.8,0.72
【解析】
(1)

(2)
(II)考慮 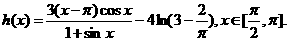
令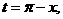 則
則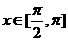 時,
時,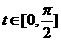
記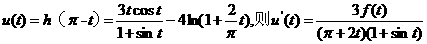
由(I)得,當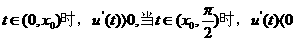
在(0,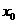 )上
)上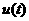 是增函數,又
是增函數,又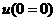 ,從而當
,從而當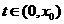 時,
時,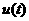
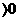 ,所以
,所以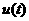 在
在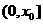 上無零點。
上無零點。
在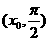 上
上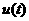 為減函數,由
為減函數,由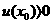 ,
,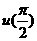 =-4ln2
=-4ln2 ,知存在唯一
,知存在唯一 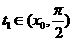 ,使
,使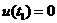 .
.
所以存在唯一的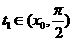 ,使
,使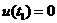 .
.
因此存在唯一的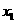 ,使
,使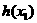 =
=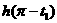 =
=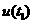 =0.
=0.
因為當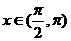 時,
時,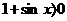 ,故
,故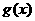 =(
=(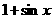 )
)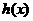 與
與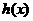 有相同的零點,所以存在唯一的
有相同的零點,所以存在唯一的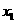
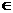
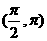 ,使
,使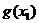 =0.
=0.
請考生在第22、23、24三題中任選一題作答,如果多做,則按所做的第一題記分,作答時用2B鉛筆在答題卡上把所選題目對應題號下方的方框涂黑.
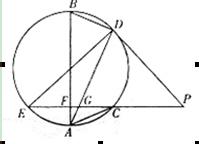
22. (本小題滿分10分)選修4-1:幾何證明選講
如圖,EP交圓于E、C兩點,PD切圓于D,G為CE上一點且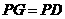 ,連接DG并延長交圓于點A,作弦AB垂直EP,垂足為F.
,連接DG并延長交圓于點A,作弦AB垂直EP,垂足為F.
(1)求證:AB為圓的直徑;
(2)若AC=BD,求證:AB=ED.
【答案】
【解析】
(1)
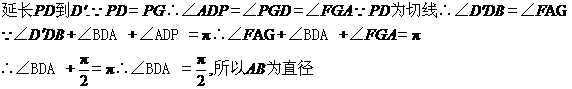
(2)
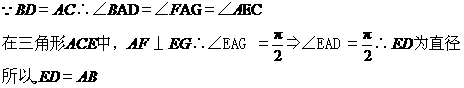
23. (本小題滿分10分)選修4-4:坐標系與參數方程
將圓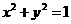 上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
(1)寫出C的參數方程;
(2)設直線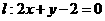 與C的交點為
與C的交點為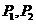 ,以坐標原點為極點,x軸正半軸為極坐標建立極坐標系,求過線段
,以坐標原點為極點,x軸正半軸為極坐標建立極坐標系,求過線段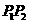 的中點且與
的中點且與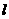 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
【答案】 (1) 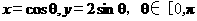 (2)
(2) 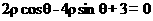
【解析】
(1)
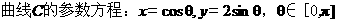
(2)

24. (本小題滿分10分)選修4-5:不等式選講
設函數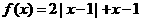 ,
,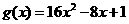 ,記
,記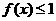 的解集為M,
的解集為M,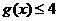 的解集為N.
的解集為N.
(1)求M;
(2)當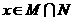 時,證明:
時,證明: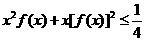 .
.
【答案】 (1) 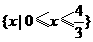 (2)
(2)
【解析】
(1)
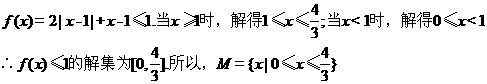
(2)