19.(本小題滿分13分)
某地建一座橋,兩端的橋墩已建好,這兩墩相距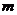 米,余下工程只需要建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為256萬元,距離為
米,余下工程只需要建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為256萬元,距離為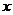 米的相鄰兩墩之間的橋面工程費用為
米的相鄰兩墩之間的橋面工程費用為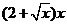 萬元。假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為
萬元。假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為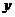 萬元。
萬元。
(Ⅰ)試寫出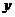 關于
關于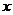 的函數關系式;
的函數關系式;
(Ⅱ)當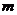 =640米時,需新建多少個橋墩才能使
=640米時,需新建多少個橋墩才能使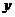 最小?
最小?
解 (Ⅰ)設需要新建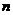 個橋墩,
個橋墩,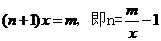
所以 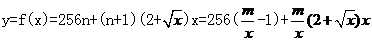
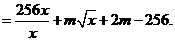
(Ⅱ) 由(Ⅰ)知,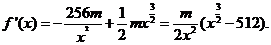
令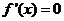 ,得
,得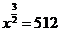 ,所以
,所以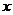 =64
=64
當0<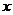 <64時
<64時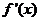 <0,
<0, 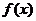 在區間(0,64)內為減函數;
在區間(0,64)內為減函數; 

當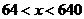 時,
時,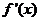 >0.
>0. 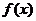 在區間(64,640)內為增函數,
在區間(64,640)內為增函數,
所以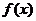 在
在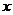 =64處取得最小值,此時,
=64處取得最小值,此時,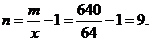
故需新建9個橋墩才能使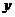 最小。
最小。
20(本小題滿分13分)
在平面直角坐標系xOy中,點P到點F(3,0)的距離的4倍與它到直線x=2的距離的3倍之和記為d,當P點運動時,d恒等于點P的橫坐標與18之和
(Ⅰ)求點P的軌跡C;
(Ⅱ)設過點F的直線I與軌跡C相交于M,N兩點,求線段MN長度的最大值。
解(Ⅰ)設點P的坐標為(x,y),則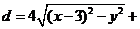 3︳x-2︳
3︳x-2︳
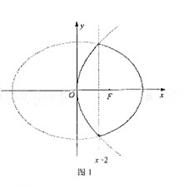 由題設
由題設
當x>2時,由①得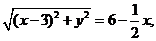
化簡得 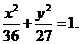
當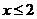 時 由①得
時 由①得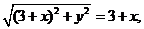
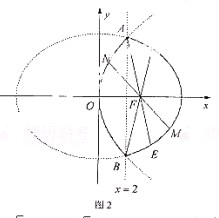
化簡得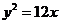
故點P的軌跡C是橢圓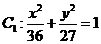 在直線x=2的右側部分與拋物線
在直線x=2的右側部分與拋物線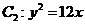 在直線x=2的左側部分(包括它與直線x=2的交點)所組成的曲線,參見圖1
在直線x=2的左側部分(包括它與直線x=2的交點)所組成的曲線,參見圖1
(Ⅱ)如圖2所示,易知直線x=2與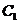 ,
,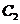 的交點都是A(2,
的交點都是A(2,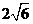 ),
),
B(2,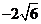 ),直線AF,BF的斜率分別為
),直線AF,BF的斜率分別為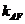 =
=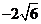 ,
,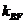 =
=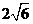 .
.
當點P在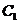 上時,由②知
上時,由②知
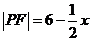 . ④
. ④
當點P在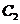 上時,由③知
上時,由③知
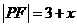 ⑤
⑤
若直線l的斜率k存在,則直線l的方程為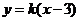
(i)當k≤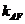 ,或k≥
,或k≥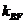 ,即k≤-2
,即k≤-2 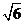 時,直線I與軌跡C的兩個交點M(
時,直線I與軌跡C的兩個交點M(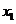 ,
,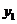 ),N(
),N(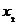 ,
,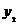 )都在C
)都在C 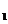 上,此時由④知
上,此時由④知
∣MF∣= 6 - 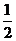
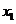 ∣NF∣= 6 -
∣NF∣= 6 - 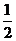
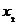
從而∣MN∣= ∣MF∣+ ∣NF∣= (6 - 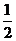
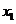 )+ (6 -
)+ (6 - 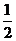
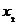 )=12 -
)=12 - 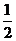 (
( 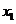 +
+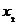 )
)
由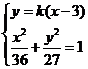 得
得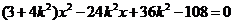 則
則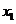 ,
,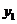 是這個方程的兩根,所以
是這個方程的兩根,所以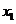 +
+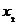 =
=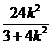 *∣MN∣=12 -
*∣MN∣=12 - 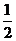 (
(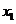 +
+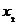 )=12 -
)=12 - 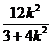
因為當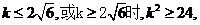
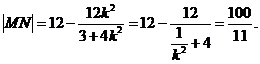

當且僅當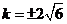 時,等號成立。
時,等號成立。
(2)當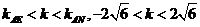 時,直線L與軌跡C的兩個交點
時,直線L與軌跡C的兩個交點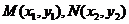 分別在
分別在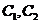 上,不妨設點
上,不妨設點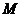 在
在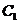 上,點
上,點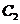 上,則④⑤知,
上,則④⑤知,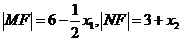
設直線AF與橢圓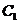 的另一交點為E
的另一交點為E
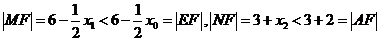
所以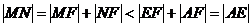 。而點A,E都在
。而點A,E都在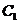 上,且
上,且
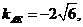 有(1)知
有(1)知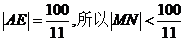

若直線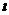 的斜率不存在,則
的斜率不存在,則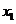 =
=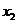 =3,此時
=3,此時
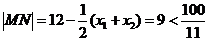
綜上所述,線段MN長度的最大值為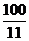
21.(本小題滿分13分)
對于數列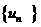 若存在常數M>0,對任意的
若存在常數M>0,對任意的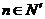 ,恒有
,恒有
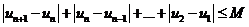

則稱數列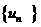 為B-數列
為B-數列
(1) 首項為1,公比為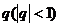 的等比數列是否為B-數列?請說明理由;
的等比數列是否為B-數列?請說明理由;
請以其中一組的一個論斷條件,另一組中的一個論斷為結論組成一個命題
判斷所給命題的真假,并證明你的結論;
(2) 設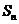 是數列
是數列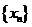 的前
的前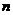 項和,給出下列兩組論斷;
項和,給出下列兩組論斷;
A組:①數列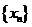 是B-數列 ②數列
是B-數列 ②數列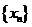 不是B-數列
不是B-數列
B組:③數列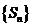 是B-數列 ④數列
是B-數列 ④數列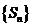 不是B-數列
不是B-數列
請以其中一組中的一個論斷為條件,另一組中的一個論斷為結論組成一個命題。
判斷所給命題的真假,并證明你的結論;
(3) 若數列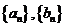 都是
都是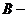 數列,證明:數列
數列,證明:數列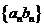 也是
也是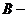 數列。
數列。
解(1)設滿足題設的等比數列為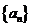 ,則
,則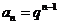 ,于是
,于是
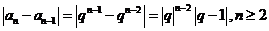
因此|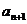 -
- 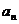 |+|
|+|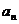 -
-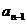 |+…+|
|+…+|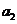 -
-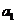 |=
|=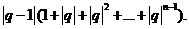
因為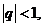 所以
所以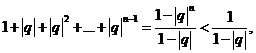 即
即
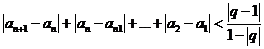
故首項為1,公比為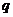
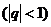 的等比數列是B-數列。
的等比數列是B-數列。
(2)命題1:若數列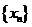 是B-數列,則數列
是B-數列,則數列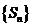 是B-數列
是B-數列
次命題為假命題。
事實上,設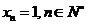 ,易知數列
,易知數列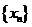 是B-數列,但
是B-數列,但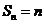
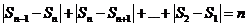
由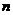 的任意性知,數列
的任意性知,數列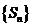 是B-數列此命題為。
是B-數列此命題為。
命題2:若數列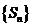 是B-數列,則數列
是B-數列,則數列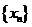 是B-數列
是B-數列
此命題為真命題
事實上,因為數列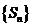 是B-數列,所以存在正數M,對任意的
是B-數列,所以存在正數M,對任意的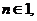 有
有
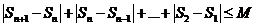

即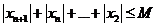 。于是
。于是
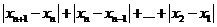
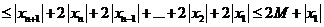
所以數列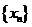 是B-數列。
是B-數列。
(III)若數列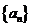 {
{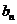 }是
}是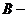 數列,則存在正數
數列,則存在正數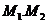 ,對任意的
,對任意的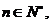 有
有
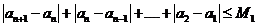
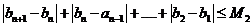
注意到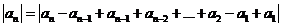
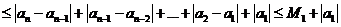
同理: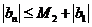
記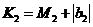 ,則有
,則有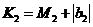
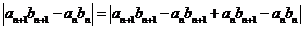
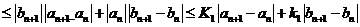
因此 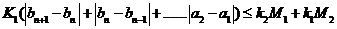
+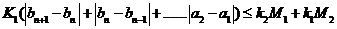
故數列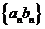 是
是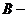 數列
數列











