一、選擇題:本大題共8小題,每小題5分,共40分。在每小題給出的四個選項中,只有一項是符合題目要求的。
1.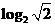 的值為 【 D 】
的值為 【 D 】
A.-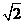 B.
B. 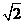 C.
C. 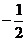 D.
D. 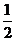
2. 拋物線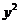 =-8x的焦點坐標(biāo)是 【 B 】
=-8x的焦點坐標(biāo)是 【 B 】

A.(2,0) B. (- 2,0) C. (4,0) D. (- 4,0)
3.設(shè)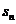 是等差數(shù)列{
是等差數(shù)列{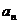 }的前n項和,已知
}的前n項和,已知 =3,
=3,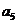 =11,則
=11,則 等于 【 C 】
等于 【 C 】
A.13 B. 35 C. 49 D. 63

4.如圖1 D,E,F(xiàn)分別是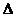 ABC的邊AB,BC,CA的中點,則 【 A 】
ABC的邊AB,BC,CA的中點,則 【 A 】
A.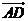 +
+  +
+  =0
=0
B.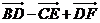 =0
=0

C.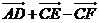 =0
=0
D. =0 圖1
=0 圖1
5.某地政府召集5家企業(yè)的負(fù)責(zé)人開會,其中甲企業(yè)有2人到會,其余4家企業(yè)各有1人到會,會上有3人發(fā)言,則這3人來自3家不同企業(yè)的可能情況的種數(shù)為【 B 】
A.14 B. 16 C. 20 D. 48
6.平面六面體 -
- 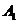
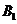
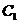
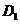 中,既與
中,既與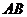 共面也與
共面也與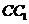 共面的棱的條數(shù)為【 C 】
共面的棱的條數(shù)為【 C 】
A.3 B. 4 C.5 D. 6

7.若函數(shù)y=f(x)導(dǎo)函數(shù)在區(qū)間[a,b]是增函數(shù),則函數(shù)y=f(x)在區(qū)間[a,b]上的圖象可能是(A)

8. 設(shè)函數(shù) 在
在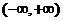 內(nèi)有定義,對于給定的正數(shù)K,定義函數(shù)
內(nèi)有定義,對于給定的正數(shù)K,定義函數(shù)


取函數(shù) 。當(dāng)
。當(dāng)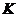 =
=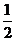 時,函數(shù)
時,函數(shù) 的單調(diào)遞增區(qū)間為 【C】
的單調(diào)遞增區(qū)間為 【C】
A  B
B 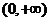 C
C  D
D 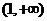
二 填空題:本大題共七小題,沒小題5分,共35分,把答案填在答題卡中對應(yīng)題號后的橫線上。
9 . 某班共30人,其中15人喜愛籃球運動,10人喜愛乒乓球運動,8人對這兩項運都不喜愛,則喜愛籃球運動但不喜愛乒乓球運動的人數(shù)為 12 .
10. 若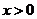 ,則
,則 的最小值為
的最小值為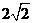 .
.
11. 在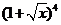 的展開式中,
的展開式中,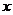 的系數(shù)為 6 (用數(shù)字作答)。
的系數(shù)為 6 (用數(shù)字作答)。
12 . 一個總體分為A.B兩層,用分層抽樣方法從總體中抽取一個容量為10的樣本。已知B層中每個個體被抽到的概率都為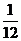 ,則總體中的個體數(shù)為 120
,則總體中的個體數(shù)為 120
13. 過雙曲線C:
 的一個焦點作圓
的一個焦點作圓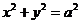 的兩條切線,切點分別為A.B,若
的兩條切線,切點分別為A.B,若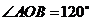 (O是坐標(biāo)原點),則雙曲線線C的離心率為 2 。
(O是坐標(biāo)原點),則雙曲線線C的離心率為 2 。
14. 在銳角 中,
中, 則
則 的值等于 2 ,
的值等于 2 ,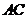 的取值范圍為
的取值范圍為 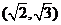 。
。
15. 如圖2,兩塊斜邊長相等的直角三角板在一起,若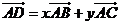 ,則
,則
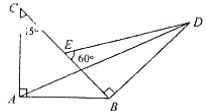
 ,
, .
. 

圖2
三 解答題:每小題共6小題,共75分,解答應(yīng)寫出文字說明.證明過程或演算步驟。
 16 (每小題滿分12分)
16 (每小題滿分12分)
以知向量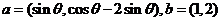 。
。
(Ⅰ)若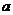 //
//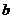 ,求
,求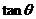 的值;
的值;
(Ⅱ)若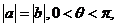 求
求 的值。
的值。

解(Ⅰ) 因為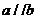 ,所以
,所以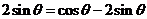 ,于是
,于是  ,故tan
,故tan =
=
(Ⅱ)由 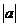 =
=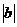 知,
知,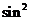
 +(cos
+(cos -2sin
-2sin
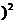 =5,所以
=5,所以
1-2sin2 +4
+4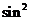
 =5.
=5.
從而-2sin2 +2(1-cos2
+2(1-cos2 =4,即sin2
=4,即sin2 +cos2
+cos2 = -1,于是
= -1,于是
Sin(2 +
+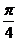 )= -
)= - 
又由0< <
<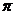 知,
知, 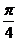 <2
<2 +
+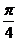 <
<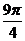 ,所以2
,所以2 +
+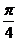 =
= ,或2
,或2 -
-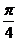 =
=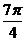
因此 =
=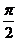 ,或
,或 =
=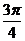


17.(本小題滿分12分)
為拉動經(jīng)濟增長,某市決定新建一批重點工程,分別為基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程三類,這三類工程所含項目的個數(shù)分別占總數(shù)的.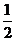 、
、 、
、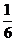 ,現(xiàn)在3名工人獨立地從中任意一個項目參與建設(shè)要求:
,現(xiàn)在3名工人獨立地從中任意一個項目參與建設(shè)要求:
(I)他們選擇的項目所屬類別互不相同的概率;

(II)至少有1人選擇的項目屬于民生工程的概率。
解:記第1名工人選擇的項目屬于基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程分別為事件 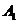 ,
,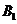 ,
,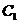 ,i=1,2,3.由題意知
,i=1,2,3.由題意知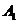
 相互獨立,
相互獨立,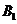
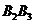 相互獨立,
相互獨立,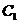
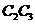 相互獨立,
相互獨立,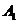 ,
,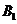 ,
,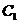 (i,j,k=1,2,3,且i,j,k互不相同)相互獨立,
(i,j,k=1,2,3,且i,j,k互不相同)相互獨立,
且P(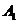 )=,p(
)=,p(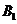 )=
)= ,p(
,p(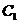 )=
)=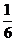


(1)他們選擇的項目所屬類別互不相同的概率
P=3!p(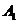

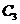 )=6p(
)=6p(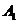 )p(
)p( )p(
)p(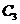 )
)
=6x 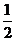 x
x x
x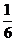 =
=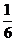
(1I)至少有1人選擇的項目屬于民生工程的概率
P=1-p(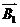

 )
)

=1-p(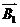 )p(
)p( )p(
)p( )
)
=1-(1-
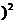 =
=