一、選擇題:本大題共9小題,每小題5分,共45分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.復數z=i·(1+i)(i為虛數單位)在復平面上對應的點位于___ B ____
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【解析】 z = i·(1+i) = i – 1.所以對應點(-1,1).選B
2.“1<x<2”是“x<2”成立的___ A ____
A.充分不必要條件 B.必要不充分條件
C.充分必要條件 D.既不充分也不必要條件
【答案】A
【解析】 若“1<x<2”成立,則“x<2”成立,所以“1<x<2”是“x<2”的充分條件;
若“x<2” 成立,則“1<x<2”不一定成立, 所以“1<x<2”不是“x<2”的必要條件.
綜上,“1<x<2”是“x<2”的充分不必要條件.
選A
3.某工廠甲、乙、丙三個車間生產了同一種產品,數量分別為120件,80件,60件。為了解它們的產品質量是否存在顯著差異,用分層抽樣方法抽取了一個容量為n的樣本進行調查,其中從丙車間的產品中抽取了3件,則n=___ D ____
A.9 B.10 C.12 D.13
【答案】D
【解析】 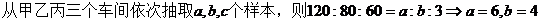
n = a + b + c=13.
選D
4.已知f(x)是奇函數,g(x)是偶函數,且f(-1)+g(1)=2,f(1)+g(-1)=4,則g(1)等于____ B ____
A.4 B.3 C.2 D.1
【答案】 B
【解析】 由題知f(-1)+g(1)= - f(1)+g(1)= 2,
f(1)+g(-1)= f(1)+ g(1)= 4.上式相加,解得g(1) = 3 .
選B
5.在銳角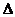 ABC中,角A,B所對的邊長分別為a,b. 若2sinB=
ABC中,角A,B所對的邊長分別為a,b. 若2sinB=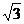 b,則角A等于____ A ____
b,則角A等于____ A ____
A.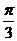 B.
B.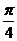 C.
C.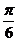 D.
D.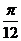
【答案】 A
【解析】 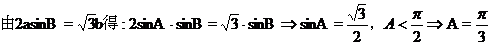
選A
6.函數f(x)=㏑x的圖像與函數g(x)=x2-4x+4的圖像的交點個數為____ C ____
A.0 B.1 C.2 D.3
【答案】 C
【解析】 在同一坐標系中畫出對數函數f(x)=㏑x的圖像和二次函數g(x)=x2-4x+4的圖像,觀察可知交點個數為2個。
選C
7.已知正方體的棱長為1,其俯視圖是一個面積為1的正方形,側視圖是一個面積為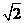 的矩形,則該正方體的正視圖的面積等于____ D ____
的矩形,則該正方體的正視圖的面積等于____ D ____
A. 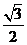 B.1 C.
B.1 C.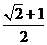 D.
D.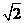
【答案】 D
【解析】 正方體的側視圖面積為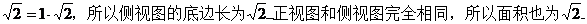 選D
選D
8.已知a,b是單位向量,a·b=0.若向量c滿足|c-a-b|=1,則|c|的最大值為____ C ____
A.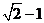 B.
B.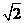 C.
C.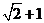 D.
D.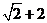
【答案】 C
【解析】  可以這樣認為:在直角坐標系中,
可以這樣認為:在直角坐標系中, 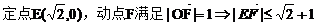
選C
9.已知事件“在矩形ABCD的邊CD上隨機取一點P,使△APB的最大邊是AB”發生的概率為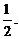 ,則
,則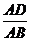 =____ D ____
=____ D ____
A.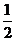 B.
B.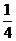 C.
C.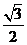 D.
D.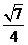
【答案】 D
【解析】 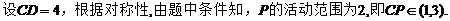
選D
二、填空題:本大題共6小題,每小題5分,共30分。
10.已知集合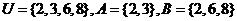 ,則
,則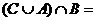 __
__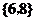 ___
___
【答案】 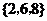
【解析】 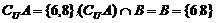 .
.
11.在平面直角坐標系xOy中,若直線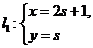 (s為參數)和直線
(s為參數)和直線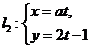 (t為參數)平行,則常數a的值為___4___
(t為參數)平行,則常數a的值為___4___
【答案】 4
【解析】 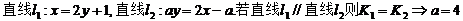 .
.
12.執行如圖1所示的程序框圖,如果輸入a=1,b=2,則輸出的a的值為____9___
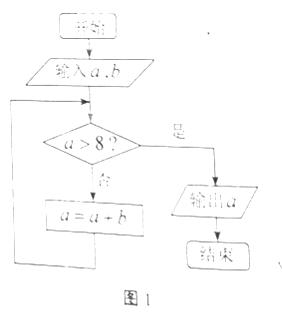
【答案】 4
【解析】 a = a + b + b + b…… = 1+2+2+2+2=9.
13.若變量x,y滿足約束條件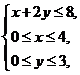 則x+y的最大值為___6___
則x+y的最大值為___6___
【答案】 6
【解析】 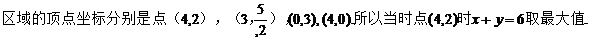
14.設F1,F2是雙曲線C,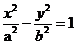 (a>0,b>0)的兩個焦點。若在C上存在一點P。使
(a>0,b>0)的兩個焦點。若在C上存在一點P。使
PF1⊥PF2,且∠PF1F2=30°,則C的離心率為____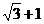 _______.
_______.
【答案】 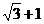
【解析】 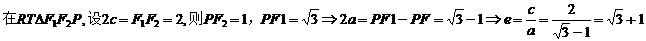
15.對于E={a1,a2,….a100}的子集X={a1,a2,…,an},定義X的“特征數列”
為x1,x2…,x100,其中x1=x10=…xn=1.其余項均為0,例如子集{a2,a3}的
“特征數列”為0,1,0,0,…,0
(1) 子集{a1,a3,a5}的“特征數列”的前三項和等于_____2________;
(2) 若E的子集P的“特征數列”P1,P2,…,P100 滿足P1+Pi+1=1, 1≤i≤99;
E 的子集Q的“特征數列” q1,q2,q100 滿足q1=1,q1+qj+1+qj+2=1,
1≤j≤98,則P∩Q的元素個數為___17______.
【答案】 (1) 2 (2)
【解析】 (1) 由題知,特征數列為:1,0,1,0,1,0,0,0……0.所以前3項和 = 2。
(2) P的“特征數列”:1,0,1,0 … 1,0. 所以P = 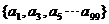 .
.
Q的“特征數列”:1,0,0,1,0,0 …1,0,0,1. 所以Q = 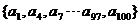 .
.
所以, 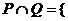
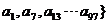 ,共有17個元素。
,共有17個元素。











