一、選擇題:本大題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.設集合M={-1,0,1},N={x|x2≤x},則M∩N=
A.{0} B.{0,1} C.{-1,1} D.{-1,0,0}
【答案】B
【解析】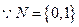 M={-1,0,1}
M={-1,0,1} 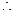 M∩N={0,1}.
M∩N={0,1}.
【點評】本題考查了集合的基本運算,較簡單,易得分.
先求出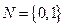 ,再利用交集定義得出M∩N.
,再利用交集定義得出M∩N.
【答案】C
【解析】因為“若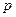 ,則
,則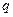 ”的逆否命題為“若
”的逆否命題為“若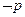 ,則
,則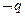 ”,所以 “若α=
”,所以 “若α=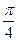 ,則tanα=1”的逆否命題是 “若tanα≠1,則α≠
,則tanα=1”的逆否命題是 “若tanα≠1,則α≠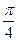 ”.
”.
【點評】本題考查了“若p,則q”形式的命題的逆命題、否命題與逆否命題,考查分析問題的能力.
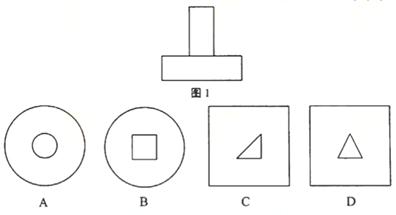
3.某幾何體的正視圖和側(cè)視圖均如圖1所示,則該幾何體的俯視圖不可能是
【答案】D
【解析】本題是組合體的三視圖問題,由幾何體的正視圖和側(cè)視圖均如圖1所示知,原圖下面圖為圓柱或直四棱柱,上面是圓柱或直四棱柱或下底是直角的三棱柱,A,B,C都可能是該幾何體的俯視圖,D不可能是該幾何體的俯視圖,因為它的正視圖上面應為如圖的矩形.
【點評】本題主要考查空間幾何體的三視圖,考查空間想象能力.是近年高考中的熱點題型.
4.設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據(jù)一組樣本數(shù)據(jù)(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為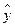 =0.85x-85.71,則下列結論中不正確的是
=0.85x-85.71,則下列結論中不正確的是
A.y與x具有正的線性相關關系
C.若該大學某女生身高增加1cm,則其體重約增加0.85kg
D.若該大學某女生身高為170cm,則可斷定其體重比為58.79kg
【答案】D
【解析】【解析】由回歸方程為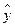 =0.85x-85.71知
=0.85x-85.71知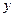 隨
隨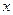 的增大而增大,所以y與x具有正的線性相關關系,由最小二乘法建立的回歸方程得過程知
的增大而增大,所以y與x具有正的線性相關關系,由最小二乘法建立的回歸方程得過程知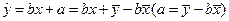 ,所以回歸直線過樣本點的中心(
,所以回歸直線過樣本點的中心(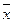 ,
,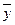 ),利用回歸方程可以預測估計總體,所以D不正確.
),利用回歸方程可以預測估計總體,所以D不正確.
【點評】本題組要考查兩個變量間的相關性、最小二乘法及正相關、負相關的概念,并且是找不正確的答案,易錯.
5. 已知雙曲線C :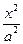 -
-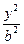 =1的焦距為10 ,點P (2,1)在C 的漸近線上,則C的方程為
=1的焦距為10 ,點P (2,1)在C 的漸近線上,則C的方程為
又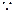 C 的漸近線為
C 的漸近線為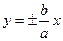 ,點P (2,1)在C 的漸近線上,
,點P (2,1)在C 的漸近線上,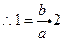 ,即
,即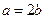 .
.
【點評】本題考查雙曲線的方程、雙曲線的漸近線方程等基礎知識,考查了數(shù)形結合的思想和基本運算能力,是近年來常考題型.
6. 函數(shù)f(x)=sinx-cos(x+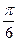 )的值域為
)的值域為
A. [ -2 ,2] B.[-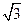 ,
,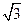 ] C.[-1,1 ] D.[-
] C.[-1,1 ] D.[-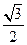 ,
, 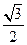 ]
]
【答案】B
【解析】f(x)=sinx-cos(x+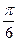 )
)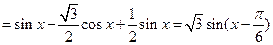 ,
,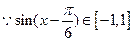 ,
,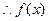 值域為[-
值域為[-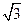 ,
,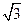 ].
].
【點評】利用三角恒等變換把 化成
化成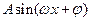 的形式,利用
的形式,利用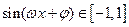 ,求得
,求得 的值域.
的值域.
7. 在△ABC中,AB=2,AC=3,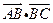 = 1則
= 1則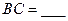 .
.
【答案】A
【解析】由下圖知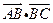

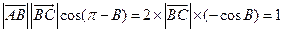 .
.
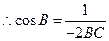 .又由余弦定理知
.又由余弦定理知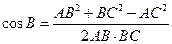 ,解得
,解得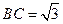 .
.
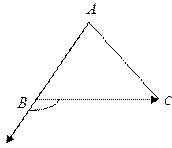
【點評】本題考查平面向量的數(shù)量積運算、余弦定理等知識.考查運算能力,考查數(shù)形結合思想、等價轉(zhuǎn)化思想等數(shù)學思想方法.需要注意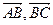 的夾角為
的夾角為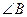 的外角.
的外角.
8.已知兩條直線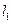 :y=m 和
:y=m 和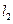 : y=
: y=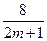 (m>0),
(m>0),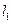 與函數(shù)
與函數(shù)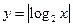 的圖像從左至右相交于點A,B ,
的圖像從左至右相交于點A,B ,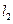 與函數(shù)
與函數(shù)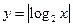 的圖像從左至右相交于C,D .記線段AC和BD在X軸上的投影長度分別為a ,b ,當m 變化時,
的圖像從左至右相交于C,D .記線段AC和BD在X軸上的投影長度分別為a ,b ,當m 變化時,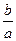 的最小值為
的最小值為
【答案】B
【解析】在同一坐標系中作出y=m,y=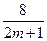 (m>0),
(m>0),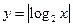 圖像如下圖,
圖像如下圖,
依照題意得
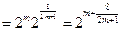 .
.
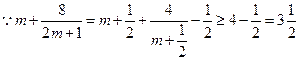 ,
,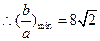 .
.
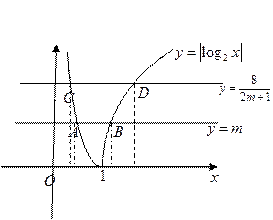


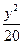
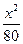
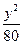
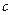 ,則
,則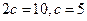 .
.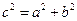 ,
,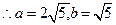 ,
,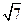
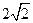
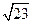
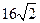
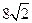
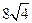
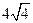
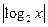 = m,得
= m,得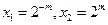 ,
,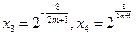 .
.








