18.(本小題滿分12分)
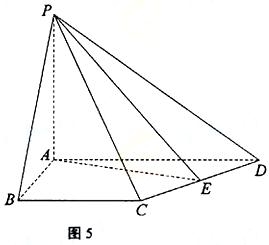
如圖5,在四棱錐P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中點.
(Ⅰ)證明:CD⊥平面PAE;
(Ⅱ)若直線PB與平面PAE所成的角和PB與平面ABCD所成的角相等,求四棱錐P-ABCD的體積.
【解析】
解法1(Ⅰ如圖(1)),連接AC,由AB=4,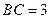 ,
,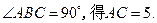
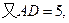 E是CD的中點,所以
E是CD的中點,所以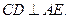
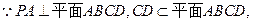 所以
所以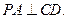
而 內的兩條相交直線,所以CD⊥平面PAE.
內的兩條相交直線,所以CD⊥平面PAE.
(Ⅱ)過點B作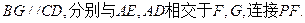
由(Ⅰ)CD⊥平面PAE知,BG⊥平面PAE.于是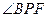 為直線PB與平面PAE
為直線PB與平面PAE
所成的角,且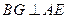 .
.
由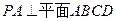 知,
知,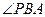 為直線
為直線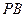 與平面
與平面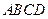 所成的角.
所成的角.
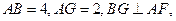 由題意,知
由題意,知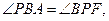
因為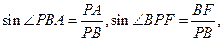 所以
所以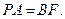
由 所以四邊形
所以四邊形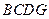 是平行四邊形,故
是平行四邊形,故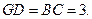 于是
于是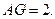
在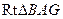 中,
中,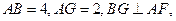 所以
所以
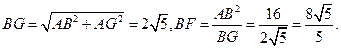
于是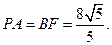
又梯形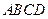 的面積為
的面積為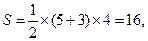 所以四棱錐
所以四棱錐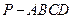 的體積為
的體積為
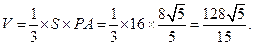
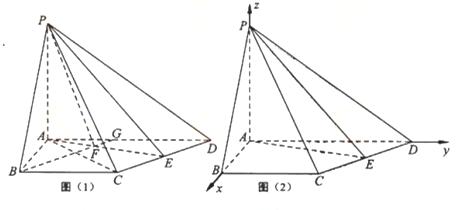
解法2:如圖(2),以A為坐標原點,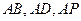 所在直線分別為
所在直線分別為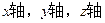 建立空間直角坐標系.設
建立空間直角坐標系.設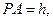 則相關的各點坐標為:
則相關的各點坐標為:
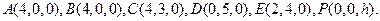
(Ⅰ)易知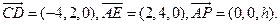 因為
因為
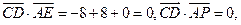 所以
所以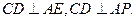 而
而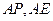 是平面
是平面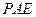 內的兩條相交直線,所以
內的兩條相交直線,所以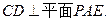
(Ⅱ)由題設和(Ⅰ)知,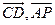 分別是
分別是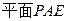 ,
,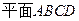 的法向量,而PB與
的法向量,而PB與
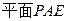 所成的角和PB與
所成的角和PB與 所成的角相等,所以
所成的角相等,所以
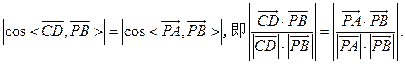
由(Ⅰ)知,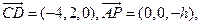 由
由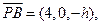 故
故
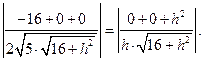
解得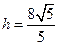 .
.
又梯形ABCD的面積為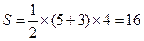 ,所以四棱錐
,所以四棱錐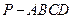 的體積為
的體積為
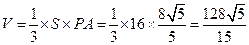 .
.
【點評】本題考查空間線面垂直關系的證明,考查空間角的應用,及幾何體體積計算.第一問只要證明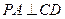 即可,第二問算出梯形的面積和棱錐的高,由
即可,第二問算出梯形的面積和棱錐的高,由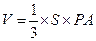 算得體積,或者建立空間直角坐標系,求得高幾體積.
算得體積,或者建立空間直角坐標系,求得高幾體積.
19.(本小題滿分12分)
已知數列{an}的各項均為正數,記A(n)=a1+a2+……+an,B(n)=a2+a3+……+an+1,C(n)=a3+a4+……+an+2,n=1,2,……
(1) 若a1=1,a2=5,且對任意n∈N﹡,三個數A(n),B(n),C(n)組成等差數列,求數列{ an }的通項公式.
(2) 證明:數列{ an }是公比為q的等比數列的充分必要條件是:對任意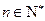 ,三個數A(n),B(n),C(n)組成公比為q的等比數列.
,三個數A(n),B(n),C(n)組成公比為q的等比數列.
【解析】
解(1)對任意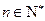 ,三個數
,三個數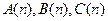 是等差數列,所以
是等差數列,所以
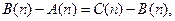
即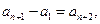 亦即
亦即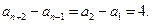
故數列 是首項為1,公差為4的等差數列.于是
是首項為1,公差為4的等差數列.于是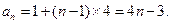
(Ⅱ)(1)必要性:若數列 是公比為q的等比數列,則對任意
是公比為q的等比數列,則對任意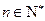 ,有
,有
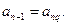 由
由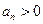 知,
知,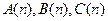 均大于0,于是
均大于0,于是
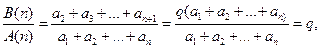
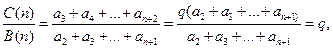
即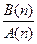 =
=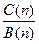 =
=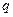 ,所以三個數
,所以三個數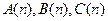 組成公比為
組成公比為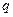 的等比數列.
的等比數列.
(2)充分性:若對于任意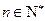 ,三個數
,三個數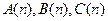 組成公比為
組成公比為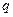 的等比數列,
的等比數列,
則
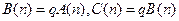 ,
,
于是 得
得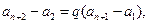 即
即
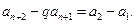
由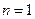 有
有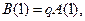 即
即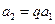 ,從而
,從而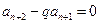 .
.
因為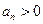 ,所以
,所以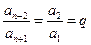 ,故數列
,故數列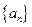 是首項為
是首項為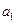 ,公比為
,公比為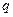 的等比數列,
的等比數列,
綜上所述,數列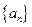 是公比為
是公比為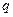 的等比數列的充分必要條件是:對任意n∈N﹡,三個數
的等比數列的充分必要條件是:對任意n∈N﹡,三個數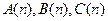 組成公比為
組成公比為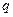 的等比數列.
的等比數列.
【點評】本題考查等差數列、等比數列的定義、性質及充要條件的證明.第一問由等差數列定義可得;第二問要從充分性、必要性兩方面來證明,利用等比數列的定義及性質易得證.
20.(本小題滿分13分)
某企業接到生產3000臺某產品的A,B,C三種部件的訂單,每臺產品需要這三種部件的數量分別為2,2,1(單位:件).已知每個工人每天可生產A部件6件,或B部件3件,或C部件2件.該企業計劃安排200名工人分成三組分別生產這三種部件,生產B部件的人數與生產A部件的人數成正比,比例系數為k(k為正整數).
(1)設生產A部件的人數為x,分別寫出完成A,B,C三種部件生產需要的時間;
(2)假設這三種部件的生產同時開工,試確定正整數k的值,使完成訂單任務的時間最短,并給出時間最短時具體的人數分組方案.
【解析】
解:(Ⅰ)設完成A,B,C三種部件的生產任務需要的時間(單位:天)分別為
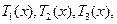 由題設有
由題設有
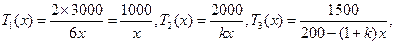
期中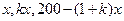 均為1到200之間的正整數.
均為1到200之間的正整數.
(Ⅱ)完成訂單任務的時間為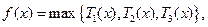 其定義域為
其定義域為
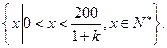 易知,
易知,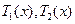 為減函數,
為減函數,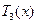 為增函數.注意到
為增函數.注意到
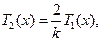 于是
于是
(1)當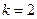 時,
時,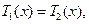 此時
此時
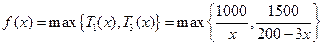 ,
,
由函數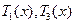 的單調性知,當
的單調性知,當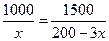 時
時 取得最小值,解得
取得最小值,解得
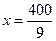 .由于
.由于
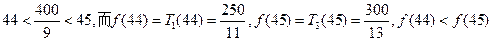 .
.
故當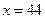 時完成訂單任務的時間最短,且最短時間為
時完成訂單任務的時間最短,且最短時間為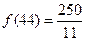 .
.
(2)當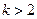 時,
時,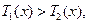 由于
由于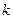 為正整數,故
為正整數,故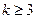 ,此時
,此時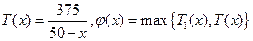 易知
易知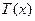 為增函數,則
為增函數,則
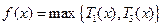
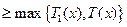
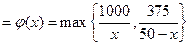 .
.
由函數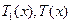 的單調性知,當
的單調性知,當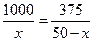 時
時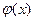 取得最小值,解得
取得最小值,解得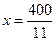 .由于
.由于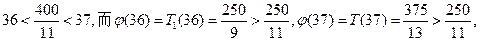
此時完成訂單任務的最短時間大于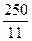 .
.
(3)當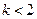 時,
時,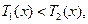 由于
由于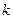 為正整數,故
為正整數,故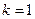 ,此時
,此時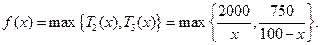 由函數
由函數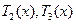 的單調性知,
的單調性知,
當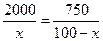 時
時 取得最小值,解得
取得最小值,解得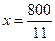 .類似(1)的討論.此時
.類似(1)的討論.此時
完成訂單任務的最短時間為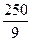 ,大于
,大于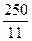 .
.
綜上所述,當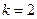 時完成訂單任務的時間最短,此時生產A,B,C三種部件的人數
時完成訂單任務的時間最短,此時生產A,B,C三種部件的人數
分別為44,88,68.
【點評】本題為函數的應用題,考查分段函數、函數單調性、最值等,考查運算能力及用數學知識分析解決實際應用問題的能力.第一問建立函數模型;第二問利用單調性與最值來解決,體現分類討論思想.
21.(本小題滿分13分)
在直角坐標系xOy中,曲線C1的點均在C2:(x-5)2+y2=9外,且對C1上任意一點M,M到直線x=﹣2的距離等于該點與圓C2上點的距離的最小值.
(Ⅰ)求曲線C1的方程;
(Ⅱ)設P(x0,y0)(y0≠±3)為圓C2外一點,過P作圓C2的兩條切線,分別與曲線C1相交于點A,B和C,D.證明:當P在直線x=﹣4上運動時,四點A,B,C,D的縱坐標之積為定值.
【解析】(Ⅰ)解法1 :設M的坐標為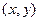 ,由已知得
,由已知得
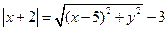 ,
,
易知圓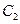 上的點位于直線
上的點位于直線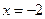 的右側.于是
的右側.于是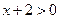 ,所以
,所以
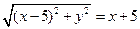 .
.
化簡得曲線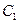 的方程為
的方程為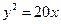 .
.
解法2 :由題設知,曲線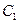 上任意一點M到圓心
上任意一點M到圓心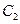
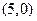 的距離等于它到直線
的距離等于它到直線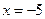 的距離,因此,曲線
的距離,因此,曲線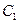 是以
是以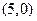 為焦點,直線
為焦點,直線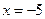 為準線的拋物線,故其方程為
為準線的拋物線,故其方程為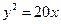 .
.
(Ⅱ)當點P在直線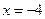 上運動時,P的坐標為
上運動時,P的坐標為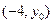 ,又
,又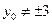 ,則過P且與圓
,則過P且與圓
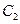 相切得直線的斜率
相切得直線的斜率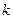 存在且不為0,每條切線都與拋物線有兩個交點,切線方程為
存在且不為0,每條切線都與拋物線有兩個交點,切線方程為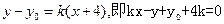 .于是
.于是
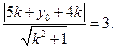
整理得
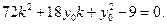 ①
①
設過P所作的兩條切線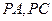 的斜率分別為
的斜率分別為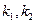 ,則
,則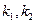 是方程①的兩個實根,故
是方程①的兩個實根,故
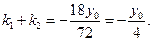 ②
②
由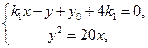 得
得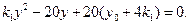 ③
③
設四點A,B,C,D的縱坐標分別為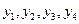 ,則是方程③的兩個實根,所以
,則是方程③的兩個實根,所以
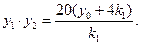 ④
④
同理可得
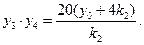 ⑤
⑤
于是由②,④,⑤三式得
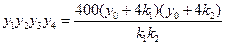
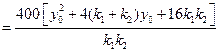
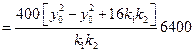 .
.
所以,當P在直線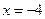 上運動時,四點A,B,C,D的縱坐標之積為定值6400.
上運動時,四點A,B,C,D的縱坐標之積為定值6400.
【點評】本題考查曲線與方程、直線與曲線的位置關系,考查運算能力,考查數形結合思想、函數與方程思想等數學思想方法.第一問用直接法或定義法求出曲線的方程;第二問設出切線方程,把直線與曲線方程聯立,由一元二次方程根與系數的關系得到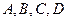 四點縱坐標之積為定值,體現“設而不求”思想.
四點縱坐標之積為定值,體現“設而不求”思想.
22.(本小題滿分13分)
已知函數 =
=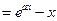 ,其中a≠0.
,其中a≠0.
(1) 若對一切x∈R, ≥1恒成立,求a的取值集合.
≥1恒成立,求a的取值集合.
(2)在函數 的圖像上取定兩點
的圖像上取定兩點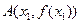 ,
,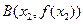
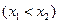 ,記直線AB的斜率為K,問:是否存在x0∈(x1,x2),使
,記直線AB的斜率為K,問:是否存在x0∈(x1,x2),使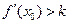 成立?若存在,求
成立?若存在,求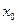 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
【解析】(Ⅰ)若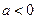 ,則對一切
,則對一切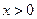 ,
,
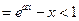 ,這與題設矛盾,又
,這與題設矛盾,又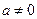 ,
,
故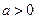 .
.
而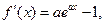 令
令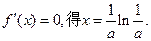
當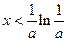 時,
時,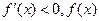 單調遞減;當
單調遞減;當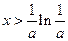 時,
時,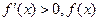 單調遞增,故當
單調遞增,故當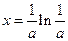 時,
時, 取最小值
取最小值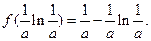
于是對一切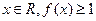 恒成立,當且僅當
恒成立,當且僅當
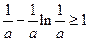 . ①
. ①
令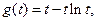 則
則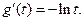
當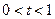 時,
時,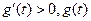 單調遞增;當
單調遞增;當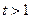 時,
時,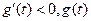 單調遞減.
單調遞減.
故當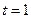 時,
時,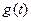 取最大值
取最大值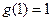 .因此,當且僅當
.因此,當且僅當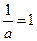 即
即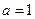 時,①式成立.
時,①式成立.
綜上所述,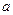 的取值集合為
的取值集合為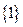 .
.
(Ⅱ)由題意知,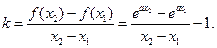
令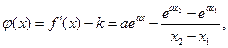 則
則
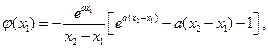
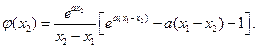
令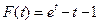 ,則
,則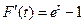 .
.
當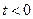 時,
時,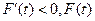 單調遞減;當
單調遞減;當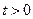 時,
時,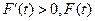 單調遞增.
單調遞增.
故當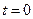 ,
,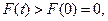 即
即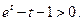
從而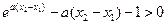 ,
,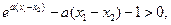 又
又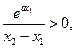
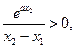
所以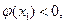
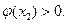
因為函數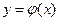 在區間
在區間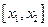 上的圖像是連續不斷的一條曲線,所以存在
上的圖像是連續不斷的一條曲線,所以存在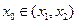 使
使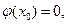
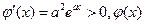 單調遞增,故這樣的
單調遞增,故這樣的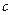 是唯一的,且
是唯一的,且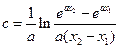 .故當且僅當
.故當且僅當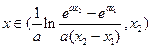 時,
時, 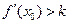 .
.
綜上所述,存在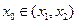 使
使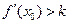 成立.且
成立.且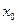 的取值范圍為
的取值范圍為
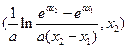 .
.
【點評】本題考查利用導函數研究函數單調性、最值、不等式恒成立問題等,考查運算能力,考查分類討論思想、函數與方程思想,轉化與劃歸思想等數學思想方法.第一問利用導函數法求出 取最小值
取最小值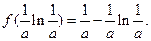 對一切x∈R,f(x)
對一切x∈R,f(x) 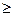 1恒成立轉化為
1恒成立轉化為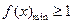 ,從而得出a的取值集合;第二問在假設存在的情況下進行推理,通過構造函數,研究這個函數的單調性及最值來進行分析判斷.
,從而得出a的取值集合;第二問在假設存在的情況下進行推理,通過構造函數,研究這個函數的單調性及最值來進行分析判斷.