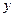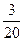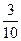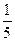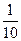二 、填空題: 本大題共8小題,考生作答7小題,每小題5分 ,共35分,把答案填在答題卡中對應題號后的橫線上.
(一)選做題(請考生在第9、10、 11三題中任選兩題作答,如果全做,則按前兩題記分 )
9. 在直角坐標系xOy 中,已知曲線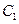 :
: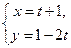 (t為參數)與曲線
(t為參數)與曲線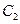 :
: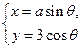
【答案】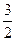
【解析】曲線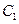 :
: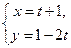 直角坐標方程為
直角坐標方程為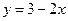 ,與
,與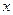 軸交點為
軸交點為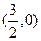 ;
;
曲線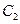 :
: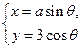 直角坐標方程為
直角坐標方程為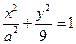 ,其與
,其與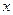 軸交點為
軸交點為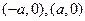 ,
,
由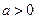 ,曲線
,曲線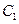 與曲線
與曲線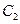 有一個公共點在X軸上,知
有一個公共點在X軸上,知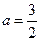 .
.
【點評】本題考查直線的參數方程、橢圓的參數方程,考查等價轉化的思想方法等.曲線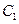 與曲線
與曲線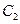 的參數方程分別等價轉化為直角坐標方程,找出與
的參數方程分別等價轉化為直角坐標方程,找出與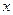 軸交點,即可求得.
軸交點,即可求得.
10.不等式|2x+1|-2|x-1|>0的解集為_______.
【答案】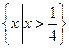
【解析】令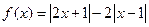 ,則由
,則由
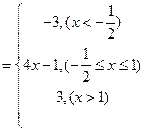 得
得
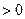 的解集為
的解集為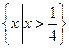 .
.
【點評】絕對值不等式解法的關鍵步驟是去絕對值,轉化為代數不等式(組).
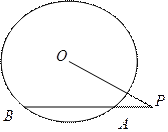
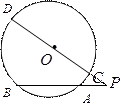
11.如圖2,過點P的直線與圓O相交于A,B兩點.若PA=1,AB=2,PO=3,則圓O的半徑等于_______.
【答案】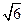
【解析】設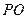 交圓O于C,D,如圖,設圓的半徑為R,由割線定理知
交圓O于C,D,如圖,設圓的半徑為R,由割線定理知
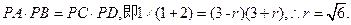
【點評】本題考查切割線定理,考查數形結合思想,由切割線定理知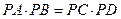 ,從而求得圓的半徑.
,從而求得圓的半徑.
(二)必做題(12~16題)
12.已知復數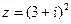 (i為虛數單位),則|z|=_____.
(i為虛數單位),則|z|=_____.
【答案】10
【解析】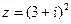 =
=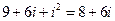 ,
,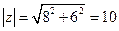 .
.
【點評】本題考查復數的運算、復數的模.把復數化成標準的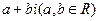 形式,利用
形式,利用
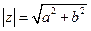 求得.
求得.
【答案】-160
【解析】( 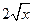 -
-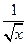 )6的展開式項公式是
)6的展開式項公式是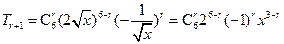 .由題意知
.由題意知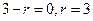 ,所以二項展開式中的常數項為
,所以二項展開式中的常數項為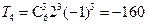 .
.
【點評】本題主要考察二項式定理,寫出二項展開式的通項公式是解決這類問題的常規辦法.
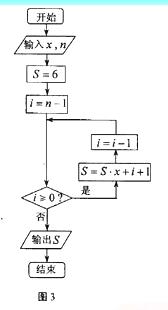
14.如果執行如圖3所示的程序框圖,輸入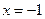 ,n=3,則輸出的數S= .
,n=3,則輸出的數S= .
【答案】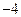
【解析】輸入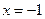 ,n=3,,執行過程如下:
,n=3,,執行過程如下: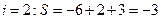 ;
;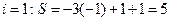 ;
;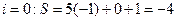 ,所以輸出的是
,所以輸出的是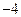 .
.
【點評】本題考查算法流程圖,要明白循環結構中的內容,一般解法是逐步執行,一步步將執行結果寫出,特別是程序框圖的執行次數不能出錯.
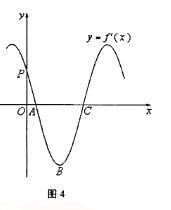
15.函數f(x)=sin (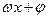 )的導函數
)的導函數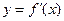 的部分圖像如圖4所示,其中,P為圖像與y軸的交點,A,C為圖像與x軸的兩個交點,B為圖像的最低點.
的部分圖像如圖4所示,其中,P為圖像與y軸的交點,A,C為圖像與x軸的兩個交點,B為圖像的最低點.
(2)若在曲線段 與x軸所圍成的區域內隨機取一點,則該點在△ABC內的概率為 .
與x軸所圍成的區域內隨機取一點,則該點在△ABC內的概率為 .
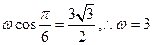 ;
;
(2)由圖知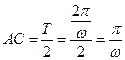 ,
,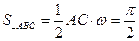 ,設
,設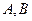 的橫坐標分別為
的橫坐標分別為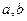 .
.
設曲線段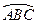 與x軸所圍成的區域的面積為
與x軸所圍成的區域的面積為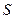 則
則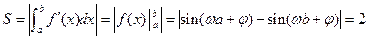 ,由幾何概型知該點在△ABC內的概率為
,由幾何概型知該點在△ABC內的概率為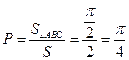 .
.
【點評】本題考查三角函數的圖像與性質、幾何概型等,(1)利用點P在圖像上求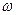 ,
,
(2)幾何概型,求出三角形面積及曲邊形面積,代入公式即得.
16.設N=2n(n∈N*,n≥2),將N個數x1,x2,…,xN依次放入編號為1,2,…,N的N個位置,得到排列P0=x1x2…xN.將該排列中分別位于奇數與偶數位置的數取出,并按原順序依次放入對應的前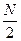 和后
和后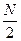 個位置,得到排列P1=x1x3…xN-1x2x4…xN,將此操作稱為C變換,將P1分成兩段,每段
個位置,得到排列P1=x1x3…xN-1x2x4…xN,將此操作稱為C變換,將P1分成兩段,每段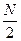 個數,并對每段作C變換,得到
個數,并對每段作C變換,得到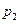 ;當2≤i≤n-2時,將Pi分成2i段,每段
;當2≤i≤n-2時,將Pi分成2i段,每段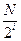 個數,并對每段C變換,得到Pi+1,例如,當N=8時,P2=x1x5x3x7x2x6x4x8,此時x7位于P2中的第4個位置.
個數,并對每段C變換,得到Pi+1,例如,當N=8時,P2=x1x5x3x7x2x6x4x8,此時x7位于P2中的第4個位置.
(1)當N=16時,x7位于P2中的第___個位置;
(2)當N=2n(n≥8)時,x173位于P4中的第___個位置.
【答案】(1)6;(2)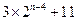
【解析】(1)當N=16時,
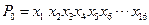 ,可設為
,可設為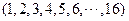 ,
,
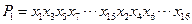 ,即為
,即為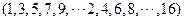 ,
,
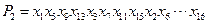 ,即
,即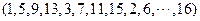 , x7位于P2中的第6個位置,;
, x7位于P2中的第6個位置,;
(2)方法同(1),歸納推理知x173位于P4中的第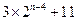 個位置.
個位置.
【點評】本題考查在新環境下的創新意識,考查運算能力,考查創造性解決問題的能力.
需要在學習中培養自己動腦的習慣,才可順利解決此類問題.
三、解答題:本大題共6小題,共75分.解答應寫出文字說明、證明過程或演算步驟.
17.(本小題滿分12分)
某超市為了解顧客的購物量及結算時間等信息,安排一名員工隨機收集了在該超市購物的100位顧客的相關數據,如下表所示.
一次購物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
顧客數(人) |
| 30 | 25 |
| 10 |
結算時間(分鐘/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知這100位顧客中的一次購物量超過8件的顧客占55%.
(Ⅰ)確定x,y的值,并求顧客一次購物的結算時間X的分布列與數學期望;
(Ⅱ)若某顧客到達收銀臺時前面恰有2位顧客需結算,且各顧客的結算相互獨立,求該顧客結算前的等候時間不超過2.5分鐘的概率.
(注:將頻率視為概率)
【解析】(1)由已知,得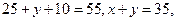 所以
所以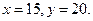
該超市所有顧客一次購物的結算時間組成一個總體,所以收集的100位顧客一次購物的結算時間可視為總體的一個容量隨機樣本,將頻率視為概率得
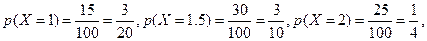
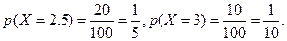
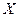 的分布為
的分布為
X | 1 | 1.5 | 2 | 2.5 | 3 |
P |
|
|
|
|
|
X的數學期望為
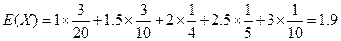 .
.
(Ⅱ)記A為事件“該顧客結算前的等候時間不超過2.5分鐘”,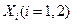 為該顧客前面第
為該顧客前面第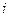 位顧客的結算時間,則
位顧客的結算時間,則
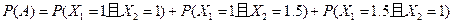 .
.
由于顧客的結算相互獨立,且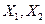 的分布列都與X的分布列相同,所以
的分布列都與X的分布列相同,所以
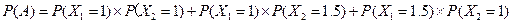
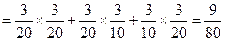 .
.
故該顧客結算前的等候時間不超過2.5分鐘的概率為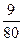 .
.
【點評】本題考查概率統計的基礎知識,考查分布列及數學期望的計算,考查運算能力、分析問題能力.第一問中根據統計表和100位顧客中的一次購物量超過8件的顧客占55%知
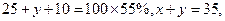 從而解得
從而解得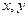 ,計算每一個變量對應的概率,從而求得分布列和期望;第二問,通過設事件,判斷事件之間互斥關系,從而求得該顧客結算前的等候時間不超過2.5分鐘的概率.
,計算每一個變量對應的概率,從而求得分布列和期望;第二問,通過設事件,判斷事件之間互斥關系,從而求得該顧客結算前的等候時間不超過2.5分鐘的概率.


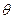
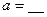 .
.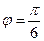 ,點P的坐標為(0,
,點P的坐標為(0,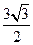
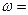 ;
;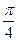
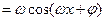 ,當
,當