三、解答題;本大題共6小題,共75分。解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟。
16.(本小題滿分12分)
已知函數(shù) f(x)=
f(x)=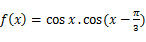
(1) 求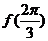 的值;
的值;
(2) 求使 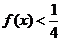 成立的x的取值集合
成立的x的取值集合
【答案】 (1) 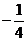 (2)
(2) 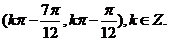
【解析】 (1) 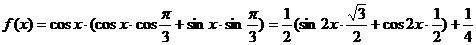
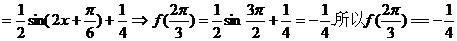 。
。
(3) 由(1)知,
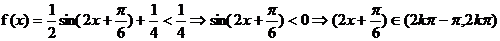
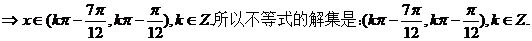
17.(本小題滿分12分)
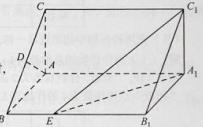
如圖2.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=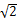 ,AA1=3,D是BC的中點(diǎn),點(diǎn)E在菱BB1上運(yùn)動(dòng)。
,AA1=3,D是BC的中點(diǎn),點(diǎn)E在菱BB1上運(yùn)動(dòng)。
(I) 證明:AD⊥C1E;
(II)當(dāng)異面直線AC,C1E 所成的角為60°時(shí),
求三菱子C1-A2B1E的體積
【答案】 (Ⅰ) 見(jiàn)下 (Ⅱ)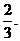
【解析】 (Ⅰ) 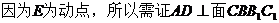 .
.
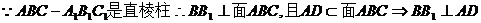
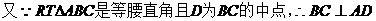 .
.
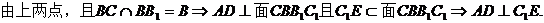 (證畢)
(證畢)
(Ⅱ)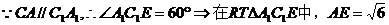 .
.
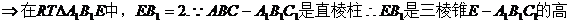 .
.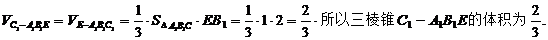
18.(本小題滿分12分)
某人在如圖3所示的直角邊長(zhǎng)為4米的三角形地塊的每個(gè)格點(diǎn)(指縱、橫直線的交叉點(diǎn)以及三角形的頂點(diǎn))處都種了一株相同品種的作物。根據(jù)歷年的種植經(jīng)驗(yàn),一株該種作物的年收貨量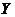 (單位:kg)與它的“相近”作物株數(shù)
(單位:kg)與它的“相近”作物株數(shù)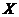 之間的關(guān)系如下表所示:
之間的關(guān)系如下表所示:
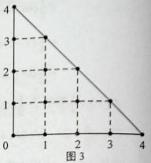

這里,兩株作物“相近”是指它們之間的直線距離不超過(guò)1米。
(Ⅰ)完成下表,并求所種作物的平均年收獲量;

(Ⅱ)在所種作物中隨機(jī)選取一株,求它的年收獲量至少為48kg的概率.
【答案】 (Ⅰ) 46 (Ⅱ)0.4
【解析】 (Ⅰ) 由圖知,三角形中共有15個(gè)格點(diǎn),
與周圍格點(diǎn)的距離不超過(guò)1米的格點(diǎn)數(shù)都是1個(gè)的格點(diǎn)有2個(gè),坐標(biāo)分別為(4,0),(0,4)。
與周圍格點(diǎn)的距離不超過(guò)1米的格點(diǎn)數(shù)都是2個(gè)的格點(diǎn)有4個(gè),坐標(biāo)分別為(0,0), (1,3), (2,2),(3,1)。
與周圍格點(diǎn)的距離不超過(guò)1米的格點(diǎn)數(shù)都是3個(gè)的格點(diǎn)有6個(gè),坐標(biāo)分別為(1,0), (2,0), (3,0),(0,1,) ,(0,2),(0,3,)。
與周圍格點(diǎn)的距離不超過(guò)1米的格點(diǎn)數(shù)都是4個(gè)的格點(diǎn)有3個(gè),坐標(biāo)分別為(1,1), (1,2), (2,1)。如下表所示:
Y | 51 | 48 | 45 | 42 |
頻數(shù) | 2 | 4 | 6 | 3 |
平均年收獲量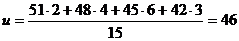 .
.
(Ⅱ)在15株中,年收獲量至少為48kg的作物共有2+4=6個(gè).
所以,15株中任選一個(gè),它的年收獲量至少為48k的概率P=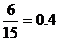 .
.
19.(本小題滿分13分)
設(shè)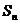 為數(shù)列{
為數(shù)列{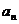 }的前項(xiàng)和,已知
}的前項(xiàng)和,已知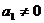 ,2
,2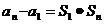 ,
,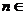 N
N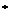
(Ⅰ)求 ,
,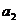 ,并求數(shù)列{
,并求數(shù)列{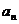 }的通項(xiàng)公式;
}的通項(xiàng)公式;
(Ⅱ)求數(shù)列{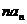 }的前
}的前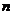 項(xiàng)和。
項(xiàng)和。
【答案】 (Ⅰ) 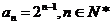 (Ⅱ)
(Ⅱ)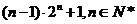
【解析】 (Ⅰ) 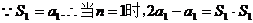
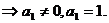
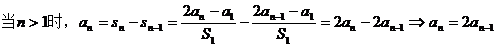 -
-
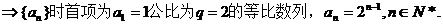
(Ⅱ)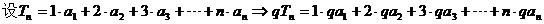
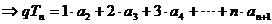
上式左右錯(cuò)位相減:
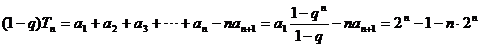
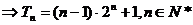 。
。
20.(本小題滿分13分)
已知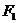 ,
,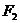 分別是橢圓
分別是橢圓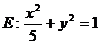 的左、右焦點(diǎn)
的左、右焦點(diǎn)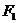 ,
,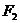 關(guān)于直線
關(guān)于直線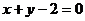 的對(duì)稱點(diǎn)是圓
的對(duì)稱點(diǎn)是圓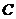 的一條直徑的兩個(gè)端點(diǎn)。
的一條直徑的兩個(gè)端點(diǎn)。
(Ⅰ)求圓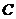 的方程;
的方程;
(Ⅱ)設(shè)過(guò)點(diǎn)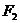 的直線
的直線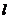 被橢圓
被橢圓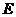 和圓
和圓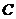 所截得的弦長(zhǎng)分別為
所截得的弦長(zhǎng)分別為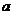 ,
,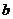 。當(dāng)
。當(dāng)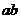 最大時(shí),求直線
最大時(shí),求直線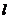 的方程。
的方程。
【答案】 (Ⅰ) 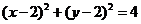 (Ⅱ)
(Ⅱ)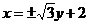
【解析】 (Ⅰ) 先求圓C關(guān)于直線x + y – 2 = 0對(duì)稱的圓D,由題知圓D的直徑為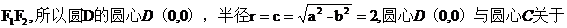 直線
直線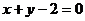 對(duì)稱
對(duì)稱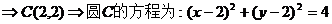 .
.
(Ⅱ)由(Ⅰ)知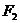 (2,0), ,據(jù)題可設(shè)直線
(2,0), ,據(jù)題可設(shè)直線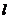 方程為: x = my +2,m∈R. 這時(shí)直線
方程為: x = my +2,m∈R. 這時(shí)直線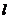 可被圓和橢圓截得2條弦,符合題意.
可被圓和橢圓截得2條弦,符合題意.
圓C: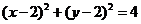 到直線
到直線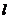 的距離
的距離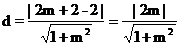 。
。
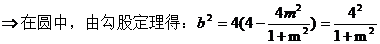 .
.
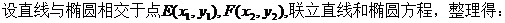
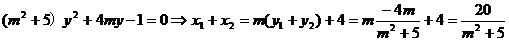
由橢圓的焦半徑公式得: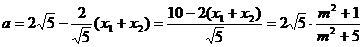
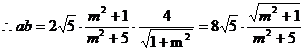 .
.
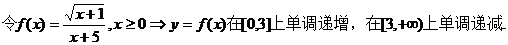

所以當(dāng)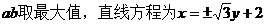
21.(本小題滿分13分
已知函數(shù)f(x)=
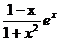 .
.
(Ⅰ)求f(x)的單調(diào)區(qū)間;
(Ⅱ)證明:當(dāng)f(x1)=f(x2)(x1≠x2)時(shí),x1+x2<0.
【答案】 (Ⅰ)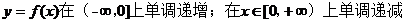 .
.
(Ⅱ)見(jiàn)下。
【解析】 (Ⅰ) 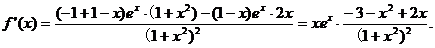
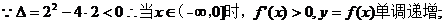
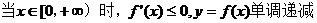 .
.
所以,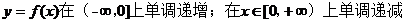 。
。
(Ⅱ)由(Ⅰ)知,只需要證明:當(dāng)x>0時(shí)f(x) < f(-x)即可。
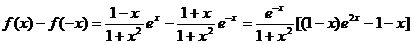 。
。
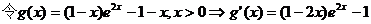 。
。
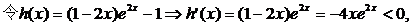
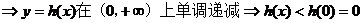
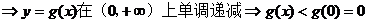
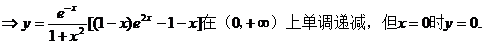
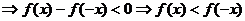
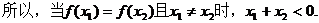 (證畢)
(證畢)











