20 (本小題滿分13分)
已知橢圓C的中心在原點(diǎn),焦點(diǎn)在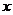 軸上,以兩個(gè)焦點(diǎn)和短軸的兩個(gè)端點(diǎn)為頂點(diǎn)的圓邊形是一個(gè)面積為8的正方形(記為Q)
軸上,以兩個(gè)焦點(diǎn)和短軸的兩個(gè)端點(diǎn)為頂點(diǎn)的圓邊形是一個(gè)面積為8的正方形(記為Q)
(1)求橢圓C的方程:

(2)設(shè)點(diǎn)P是橢圓C的左準(zhǔn)線與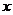 軸的交點(diǎn),過(guò)點(diǎn)P的直線L與橢圓C相交于M.N兩點(diǎn),當(dāng)線段MN的中點(diǎn)落在正方形Q內(nèi)(包括邊界)時(shí),求直線L的斜率的取值范圍。
軸的交點(diǎn),過(guò)點(diǎn)P的直線L與橢圓C相交于M.N兩點(diǎn),當(dāng)線段MN的中點(diǎn)落在正方形Q內(nèi)(包括邊界)時(shí),求直線L的斜率的取值范圍。
解 (1) 依題意,設(shè)橢圓C的方程為 焦距為
焦距為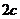 ,由題設(shè)條件知,
,由題設(shè)條件知,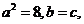 所以
所以 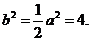 故橢圓C的方程式為
故橢圓C的方程式為


(3)橢圓C的左準(zhǔn)線方程為 所以點(diǎn)P的坐標(biāo)
所以點(diǎn)P的坐標(biāo) ,顯然直線
,顯然直線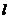 的斜率
的斜率 存在,所以直線
存在,所以直線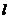 的方程為
的方程為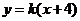 。
。

如圖,設(shè)點(diǎn)M,N的左邊分別為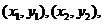 線段MN的中點(diǎn)G
線段MN的中點(diǎn)G ,
,
由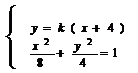 得
得
 ……①
……①
由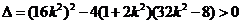 解得
解得 ……②
……②
因?yàn)?img onmouseover='upNext(this)' title="1411376332296086.gif" src="http://pic.kekenet.com/2014/0922/1411376439924410.gif" border="0"/>是方程①的兩根,所以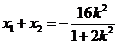 ,于是
,于是

 =
= ,
,


因?yàn)?img onmouseover='upNext(this)' title="1411376333785186.gif" src="http://pic.kekenet.com/2014/0922/1411376439823716.gif" border="0"/>
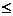 0,所以點(diǎn)G不可能在
0,所以點(diǎn)G不可能在 軸的右邊,有直線
軸的右邊,有直線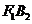 ,
,
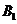 方程分
方程分
別為 所以點(diǎn)
所以點(diǎn)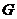 在正方形
在正方形 內(nèi)(包括邊界)的充要條件為
內(nèi)(包括邊界)的充要條件為

既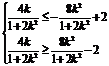 亦即
亦即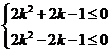


解得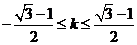 ,此時(shí)②也成立
,此時(shí)②也成立
故直線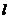 斜率的取值范圍是[
斜率的取值范圍是[ ,
, )
)
21.(本小題滿分13分)
對(duì)于數(shù)列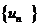 若存在常數(shù)M>0,對(duì)任意的
若存在常數(shù)M>0,對(duì)任意的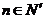 ,恒有
,恒有
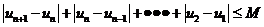


則稱數(shù)列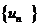 為
為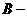 數(shù)列
數(shù)列
(I) 首項(xiàng)為1,公比為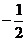 的等比數(shù)列是否為B-數(shù)列?請(qǐng)說(shuō)明理由;
的等比數(shù)列是否為B-數(shù)列?請(qǐng)說(shuō)明理由;
(II)設(shè)S 是數(shù)列
是數(shù)列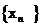 的前n項(xiàng)和。給出下列兩組判斷:
的前n項(xiàng)和。給出下列兩組判斷:
A組:①數(shù)列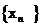 是B-數(shù)列。 ②數(shù)列
是B-數(shù)列。 ②數(shù)列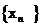 不是B-數(shù)列。
不是B-數(shù)列。
③數(shù)列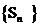 是B-數(shù)列。 ④數(shù)列
是B-數(shù)列。 ④數(shù)列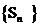 不是B-數(shù)列
不是B-數(shù)列
請(qǐng)以其中一組的一個(gè)論斷條件,另一組中的一個(gè)論斷為結(jié)論組成一個(gè)命題
判斷所給命題的真假,并證明你的結(jié)論;
(Ⅲ)若數(shù)列{a }是B
}是B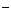 數(shù)列,證明:數(shù)列{a
數(shù)列,證明:數(shù)列{a }也是B
}也是B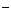 數(shù)列。
數(shù)列。

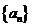 ,則
,則 ,于是
,于是



|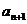 -
- 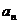 |+|
|+|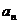 -
- |+…+|
|+…+| -
- |
|
=
=3× <3
<3
所以首項(xiàng)為1,公比為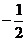 的等比數(shù)列是B-數(shù)列
的等比數(shù)列是B-數(shù)列

(Ⅱ)命題1:若數(shù)列{ }是B-數(shù)列,則數(shù)列{
}是B-數(shù)列,則數(shù)列{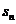 }是B-數(shù)列
}是B-數(shù)列
此命題為假命題
事實(shí)上設(shè) =1,n
=1,n N,易知數(shù)列{
N,易知數(shù)列{ }是B-數(shù)列,但
}是B-數(shù)列,但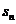 =n,
=n,
| -
- 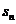 |+|
|+|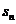 -
- |+…+|
|+…+| -
- |=n
|=n
由n有的任意性知,數(shù)列{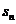 }不是B-數(shù)列。
}不是B-數(shù)列。
命題2:若數(shù)列{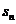 }是B-數(shù)列,則數(shù)列{
}是B-數(shù)列,則數(shù)列{ }不是B-數(shù)列。
}不是B-數(shù)列。
此命題為真命題。事實(shí)上,因?yàn)閿?shù)列{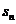 }是B-數(shù)列,所以存在正數(shù)M,對(duì)任意的n
}是B-數(shù)列,所以存在正數(shù)M,對(duì)任意的n N,有
N,有
| -
- 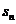 |+|
|+|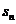 -
- |+…+|
|+…+| -
- |
|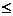 M
M

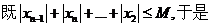

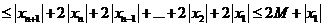
所以數(shù)列 是
是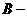 數(shù)列。
數(shù)列。
(注:按題中要求組成其它命題解答時(shí),闡述解法)
③若數(shù)列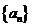 是
是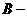 數(shù)列,則存在正數(shù)M,對(duì)任意的
數(shù)列,則存在正數(shù)M,對(duì)任意的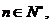 有
有

因?yàn)?img onmouseover='upNext(this)' title="1411376339756575.gif" src="http://pic.kekenet.com/2014/0922/1411376455545975.gif" border="0"/>
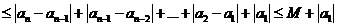
 ,則有
,則有

因此 
故數(shù)列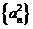 是
是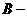 數(shù)列
數(shù)列












