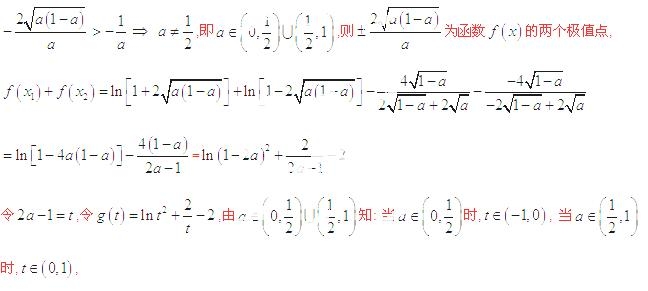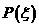一.選擇題.
1.滿足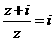 (
(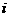 是虛數單位)的復數
是虛數單位)的復數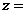 ( )
( )
A.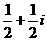 B.
B. 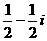 C.
C. 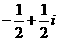 D.
D. 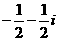
【答案】B
【解析】由題可得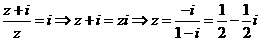 ,故選B.
,故選B.
2. 對一個容量為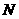 的總體抽取容量為
的總體抽取容量為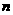 的樣本,當選取簡單隨機抽樣、系統抽樣和分層抽樣三種不同方法抽取樣本時,總體中每個個體被抽中的概率分別為
的樣本,當選取簡單隨機抽樣、系統抽樣和分層抽樣三種不同方法抽取樣本時,總體中每個個體被抽中的概率分別為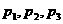 ,則( )
,則( )
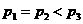 B.
B. 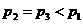 C.
C. 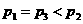 D.
D. 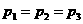

3.已 知
知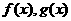 分別是定義在
分別是定義在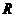 上的偶函數和奇函數,且
上的偶函數和奇函數,且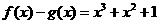 ,則
,則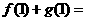
A. 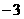 B.
B. 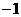 C. 1 D. 3
C. 1 D. 3

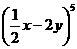 的展開式中
的展開式中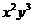 的系數是( )
的系數是( )
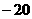 B.
B.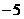
 C.5 D.20
C.5 D.20
【答案】A
【解析】第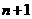 項展開式為
項展開式為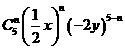 ,
,
則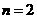 時,
時, 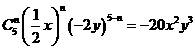 ,故選A.
,故選A.
已知命題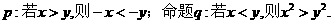 在命題
在命題
①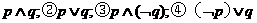 中,真命題是( )
中,真命題是( )
A①③ B.①④ C.②③ D.②④

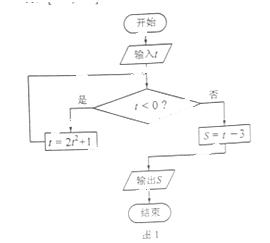
執行如圖1所示的程序框圖,如果輸入的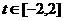 ,則輸出的S屬于( )
,則輸出的S屬于( )
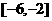 B.
B.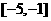 C.
C.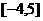 D.
D.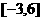
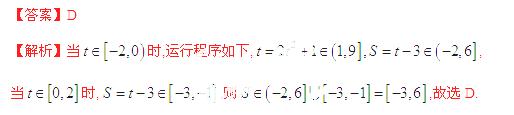
一塊石材表示的幾何體的 三視圖如圖2所示
三視圖如圖2所示 ,將該石材切削、打磨、加工成球,則能得到的最大球的半徑等于( )
,將該石材切削、打磨、加工成球,則能得到的最大球的半徑等于( )
A.1 B.2 C.3 D.4

【答案】B
【解析】最大球的半徑為正視圖直角三角形內切圓的半徑 ,則
,則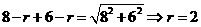 ,故選B.
,故選B.
某市生產總值連續兩年持續增加.第一年的增長率為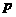 ,第二年的增長率為
,第二年的增長率為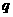 ,則該市這
,則該市這
兩年生產總值的年平均增長率為( )
 A.
A.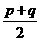 B.
B.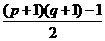
C.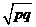 D.
D.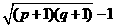
【答案】D
【解析】設兩年的平均增長率為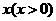 ,則有
,則有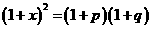
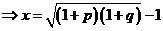 ,故選D.
,故選D.
已知函數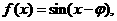 且
且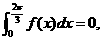 則函數
則函數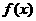 的圖象的一條對稱軸是
的圖象的一條對稱軸是
A.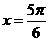 B.
B.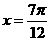 C.
C.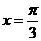 D.
D.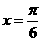

已知函數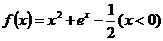 與
與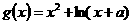 圖象上存在關于
圖象上存在關于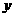 軸對稱的點,則
軸對稱的點,則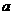 的取值范圍是( )
的取值范圍是( )
A. 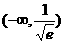 B.
B. 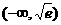 C.
C. 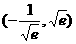 D.
D. 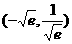

二.填空題:本大題共6小題,考生作答5小題,沒小題5分,共25分.
(一)選做題(請考生在第11,12,13三題中任選兩題作答,如果全做,則按前兩題記分)
在平面直角坐標系中,傾斜角為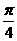 的直線
的直線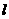 與曲線
與曲線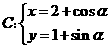 ,(
,(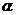 為參數)交于
為參數)交于 、
、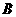 兩點,且
兩點,且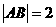 ,
, 以坐標原點
以坐標原點 為極點,
為極點,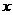 軸正半軸為極軸建立極坐標系,則直線
軸正半軸為極軸建立極坐標系,則直線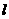 的極坐標方程是________.
的極坐標方程是________.
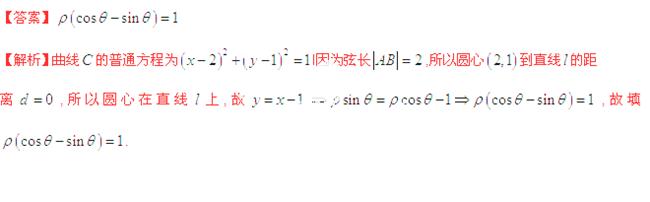
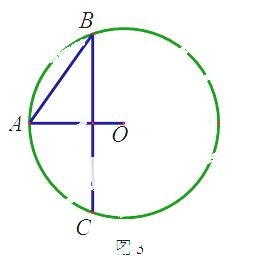
如圖3,已知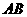 ,
,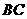 是
是 的兩條弦,
的兩條弦,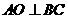 ,
,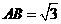 ,
,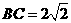 ,則
,則 的半徑等于______
的半徑等于______ __.
__.
若關于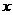 的不等式
的不等式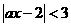 的
的 解集為
解集為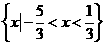 ,則
,則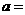 ___
___ _____.
_____.
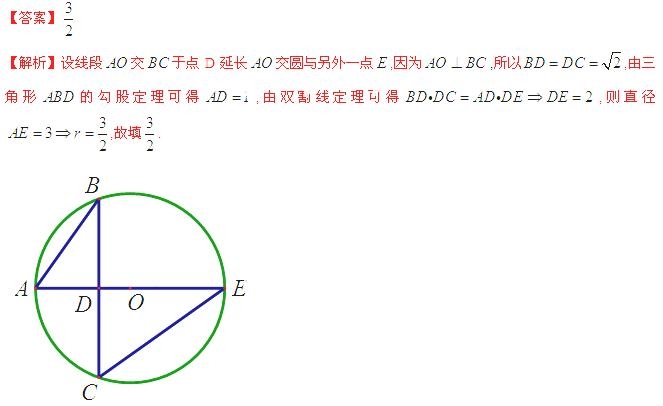
【答案】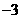
【解析】由題可得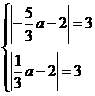
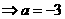 ,故填
,故填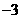 .
.
(二)必做題(14-16題)
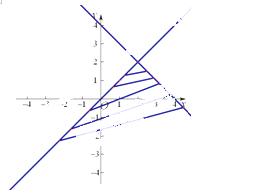
14.若變量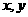 滿足約束條件
滿足約束條件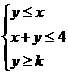 ,且
,且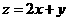 的最小值為
的最小值為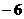 ,則
,則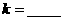

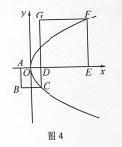
15.如圖4,正方形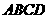 和正方形
和正方形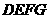 的邊長分別為
的邊長分別為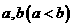 ,原點
,原點 為
為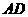 的中點,拋物線
的中點,拋物線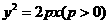 經過
經過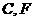 兩點,則
兩點,則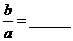 .
.
【答案】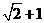
【解析】因為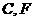 在拋物線上,所以
在拋物線上,所以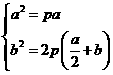
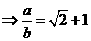 ,故填
,故填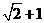 .
.
 16.在平面直角坐標系中,
16.在平面直角坐標系中, 為原點,
為原點,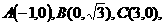 動點
動點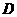 滿足
滿足 =1,則
=1,則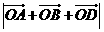
的最大值是_________.

17.某企業甲,乙兩個研發小組,他們研發新產品成功的概率分別為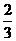 和
和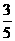 ,現安排甲組研發新產品
,現安排甲組研發新產品 ,乙組研發新產品
,乙組研發新產品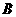 .設甲,乙兩組的研發是相互獨立的.
.設甲,乙兩組的研發是相互獨立的.
(1)求至少有一種新產品研發成功的概率;
(2)若新產品 研發成功,預計企業可獲得
研發成功,預計企業可獲得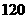 萬元,若新產品
萬元,若新產品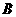 研發成功,預計企業可獲得利潤
研發成功,預計企業可獲得利潤 萬元,求該企業可獲得利潤的分布列和數學期望.
萬元,求該企業可獲得利潤的分布列和數學期望.
所以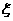 的分布列如下:
的分布列如下:
|
|
|
|
|
|
|
|
|
|
則數學期望
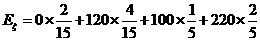
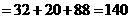 .
.
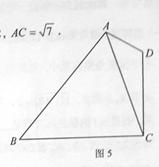
18.如圖5,在平面四邊形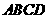 中,
中,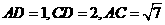 .
.
(1)求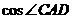 的值;
的值;
(2)若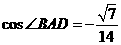 ,
,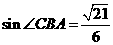 ,求
,求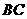 的長.
的長.

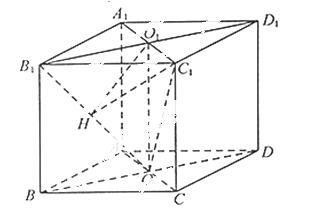
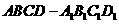 的所有棱長都相等,
的所有棱長都相等,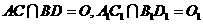 ,四邊形
,四邊形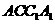 和四邊形
和四邊形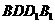 為矩形.
為矩形.(1)證明: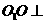 底面
底面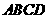 ;
;
(2)若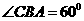 ,求二面角
,求二面角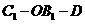 的余弦值.
的余弦值.
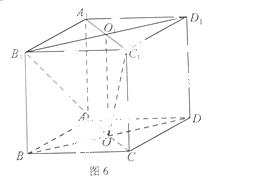

 底面
底面 .
.
(2)法1::過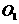 作
作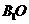 的垂線交
的垂線交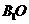 于點
于點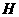 ,連接
,連接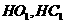 .不妨設四棱柱
.不妨設四棱柱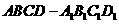 的邊長為
的邊長為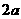
 .
.
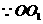
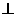 底面
底面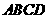 且底面
且底面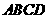
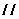 面
面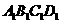


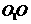
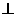 面
面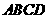 ,從而
,從而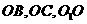 兩兩垂直,如圖以
兩兩垂直,如圖以 為坐標原點,
為坐標原點,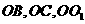 所在直線分別為
所在直線分別為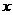 軸,
軸,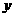

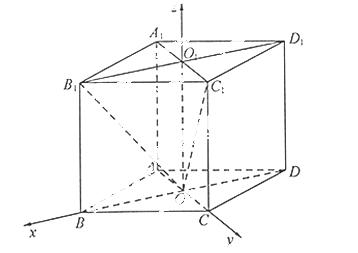
20.已知數列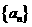 滿足
滿足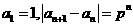 ,
,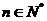 .
.
(1)若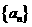 為遞增數列,且
為遞增數列,且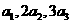 成等差數列,求
成等差數列,求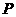 的值
的值 ;
;
(2)若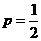 ,且
,且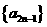 是遞增數列,
是遞增數列,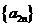 是遞減數列,求數列
是遞減數列,求數列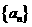 的通項公式.
的通項公式.
【答案】(1)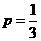 (2)
(2) 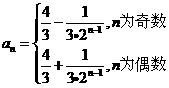 或
或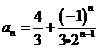
【解析】解:(1)因為數列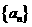 為遞增數列,所以
為遞增數列,所以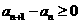 ,則
,則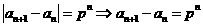 ,分別令
,分別令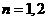 可得
可得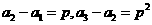
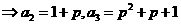 ,因為
,因為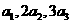 成等差數列,所以
成等差數列,所以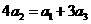
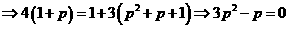
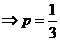 或
或 ,
,
當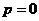 時,
時, 數列
數列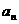 為常數數列不符合數列
為常數數列不符合數列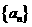 是遞增數列,所以
是遞增數列,所以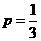 .
.


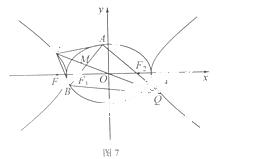
21.如圖7, 為坐標原點,橢圓
為坐標原點,橢圓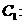
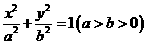 的左右焦點分別為
的左右焦點分別為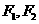 ,離心率為
,離心率為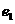 ;雙曲線
;雙曲線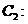
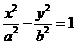 的左右焦點分別為
的左右焦點分別為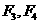 ,離心率為
,離心率為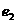 ,已知
,已知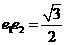 ,
, 且
且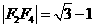 .
.
(1)求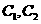 的方程;
的方程;
(2)過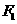 點作
點作 的不垂直于
的不垂直于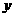 軸的弦
軸的弦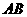 ,
,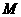 為
為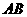 的中點,當直線
的中點,當直線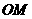 與
與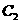 交于
交于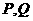 兩點時,求四邊形
兩點時,求四邊形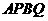 面積的最小值.
面積的最小值.

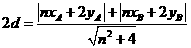 ,因為
,因為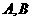 在直線
在直線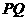 的兩端,所以
的兩端,所以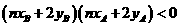 ,
,
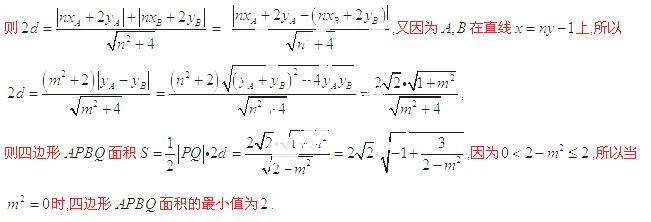
22.已知常數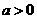 ,函數
,函數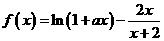 .
.
(1)討論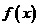 在區間
在區間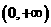 上的單調性;
上的單調性;
(2)若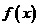 存在兩個極值點
存在兩個極值點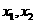 ,且
,且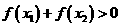 ,求
,求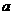 的取值范圍.
的取值范圍.

(2)函數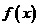 的定義域為
的定義域為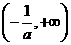 ,由(1)可得當
,由(1)可得當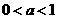 時,
時,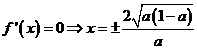 ,則
,則