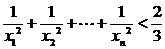2014年高考數學真題Word版(湖南卷+文科)
一.選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一項是符合題目要求的.
1.設命題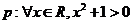 ,則
,則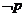 為( )
為( )
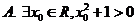
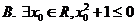
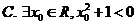
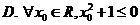
2.已知集合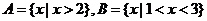 ,則
,則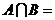 ( )
( )
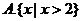
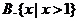
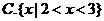
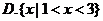
3.對一個容器為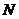 的總體抽取容量為
的總體抽取容量為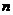 的樣本,當選取簡單隨機抽樣、系統抽樣和分層抽樣三種不同方法抽取樣本時,總體中每個個體被抽中的概率分別為
的樣本,當選取簡單隨機抽樣、系統抽樣和分層抽樣三種不同方法抽取樣本時,總體中每個個體被抽中的概率分別為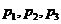 ,則( )
,則( )
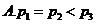
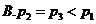
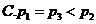
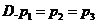
4.下列函數中,既是偶函數又在區間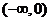 上單調遞增的是( )
上單調遞增的是( )
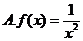
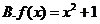
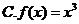
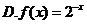
5.在區間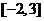 上隨機選取一個數
上隨機選取一個數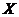 ,則
,則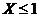 的概率為( )
的概率為( )
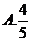
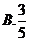
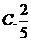
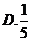
6.若圓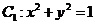 與圓
與圓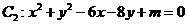 ,則
,則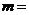 ( )
( )
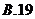
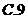
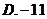
7.執行如圖1所示的程序框圖,如果輸入的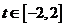 ,則輸出的
,則輸出的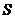 屬于( ) A.
屬于( ) A.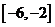 B.
B.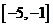 C.
C.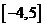 D.
D.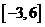
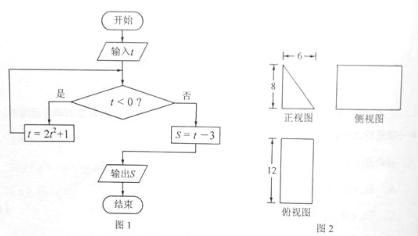
8.一塊石材表示的幾何體的三視圖如圖2所示,將石材切削、打磨、加工成球,則能得 到的最大球的半徑等于( ) A.1 B.2 C.3 D.4 9.若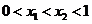 ,則( ) A.
,則( ) A. B.
B.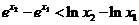 C.
C.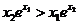 D.
D.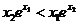
10.在平面直角坐標系中,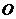 為原點,
為原點,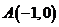 ,
,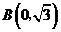 ,
,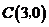 ,動點
,動點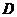 滿足
滿足 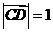 ,則
,則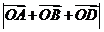 的取值范圍是( ) A.
的取值范圍是( ) A.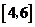 B.
B.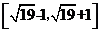 C.
C.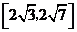 D.
D.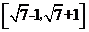
填空題:本大題共5小題,每小題5分,共25分.
復數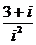 (
(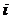 為虛數單位)的實部等于_________.
為虛數單位)的實部等于_________.
在平面直角坐標系中,曲線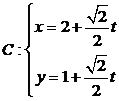 (
(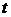 為參數)的普通方程為___________.
為參數)的普通方程為___________.
13.若變量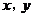 滿足約束條件
滿足約束條件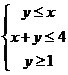 ,則
,則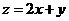 的最大值為_________.
的最大值為_________.
14.平面上以機器人在行進中始終保持與點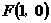 的距離和到直線
的距離和到直線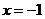 的距離相等.若
的距離相等.若
機器人接觸不到過點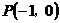 且斜率為
且斜率為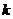 的直線,則
的直線,則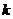 的取值范圍是___________.
的取值范圍是___________.
15.若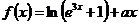 是偶函數,則
是偶函數,則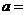 ____________.
____________.
三、解答題:本大題共6小題,共75分.解答應寫出文字說明,證明過程或演算過程.
16.(本小題滿分12分)
已知數列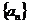 的前
的前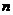 項和
項和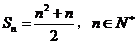 .
.
(I)求數列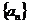 的通項公式;
的通項公式;
(II)設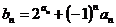 ,求數列
,求數列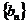 的前
的前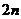 項和.
項和.
17.(本小題滿分12分)
某企業有甲、乙兩個研發小組,為了比較他們的研發水平,現隨機抽取這兩個小組往年
研發新產品的結果如下:
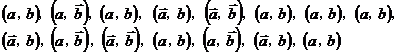
其中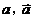 分別表示甲組研發成功和失敗;
分別表示甲組研發成功和失敗;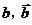 分別表示乙組研發成功和失敗.
分別表示乙組研發成功和失敗.
(I)若某組成功研發一種新產品,則給改組記1分,否記0分,試計算甲、乙兩組研
發新產品的成績的平均數和方差,并比較甲、乙兩組的研發水平;
(II)若該企業安排甲、乙兩組各自研發一種新產品,試估算恰有一組研發成功的概率.
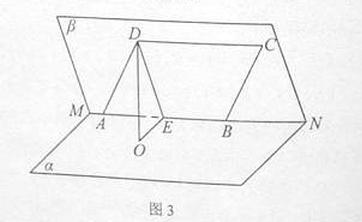
(本小題滿分12分)
如圖3,已知二面角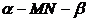 的大小為
的大小為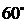 ,菱形
,菱形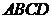 在面
在面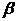 內,
內,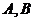 兩點在棱
兩點在棱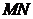 上,
上,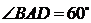 ,
,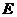 是
是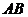 的中點,
的中點,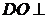 面
面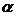 ,垂足為
,垂足為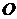 .
.
證明: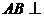 平面
平面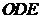 ;
;
(2)求異面直線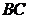 與
與 所成角的余弦值.
所成角的余弦值.
19.(本小題滿分13分)
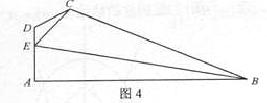
如圖4,在平面四邊形 中,
中,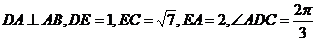 ,
,
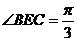
(1)求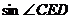 的值;
的值;
(2)求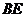 的長
的長
(本小題滿分13分)
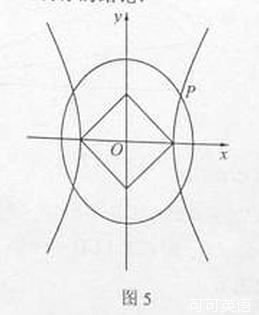
如圖5,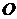 為坐標原點,雙曲線
為坐標原點,雙曲線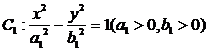 和橢圓
和橢圓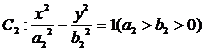 均過點
均過點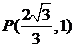 ,且以
,且以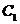 的兩個頂點和
的兩個頂點和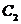 的兩個焦點為頂點的四邊形是面積為2的正方形.
的兩個焦點為頂點的四邊形是面積為2的正方形.
求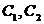 的方程;
的方程;
是否存在直線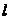 ,使得
,使得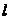 與
與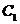 交于
交于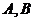 兩點,與
兩點,與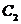 只有一個公共點,且
只有一個公共點,且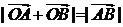 ?證明你的結論.
?證明你的結論.
21.(本小題滿分13分)
已知函數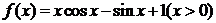 .
.
求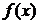 的單調區間;
的單調區間;
(2)記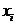 為
為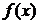 的從小到大的第
的從小到大的第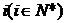 個零點,證明:對一切
個零點,證明:對一切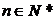 ,有
,有