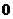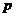三.解答題:本大題共6小題,共75分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。
16.(本小題滿分12分)
在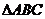 ,已知
,已知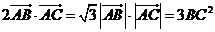 ,求角A,B,C的大小。
,求角A,B,C的大小。
解:設(shè)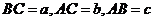
由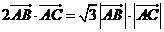 得
得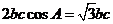 ,所以
,所以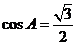
又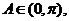 因此
因此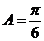

由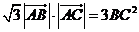 得
得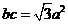 ,于是
,于是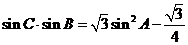
所以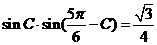 ,
,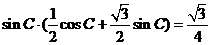 ,因此
,因此
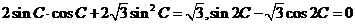 ,既
,既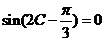
由A=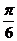 知
知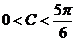 ,所以
,所以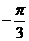 ,
,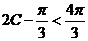 ,從而
,從而
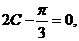 或
或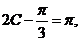 ,既
,既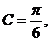 或
或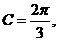 故
故
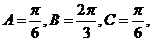 或
或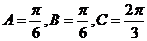 。
。
17.(本小題滿分12分)
為拉動(dòng)經(jīng)濟(jì)增長(zhǎng),某市決定新建一批重點(diǎn)工程,分別為基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程三類,這三類工程所含項(xiàng)目的個(gè)數(shù)分別占總數(shù)的.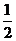 、
、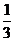 、
、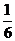 ,現(xiàn)在3名工人獨(dú)立地從中任選一個(gè)項(xiàng)目參與建設(shè)。
,現(xiàn)在3名工人獨(dú)立地從中任選一個(gè)項(xiàng)目參與建設(shè)。
(I)求他們選擇的項(xiàng)目所屬類別互不相同的概率;
(II)記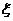 為3人中選擇的項(xiàng)目屬于基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程的人數(shù),求
為3人中選擇的項(xiàng)目屬于基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程的人數(shù),求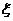 的分布列及數(shù)學(xué)期望。
的分布列及數(shù)學(xué)期望。
解:記第1名工人選擇的項(xiàng)目屬于基礎(chǔ)設(shè)施工程、民生工程和產(chǎn)業(yè)建設(shè)工程分別為事件 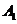 ,
,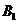 ,
,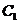 ,i=1,2,3.由題意知
,i=1,2,3.由題意知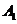
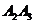 相互獨(dú)立,
相互獨(dú)立,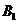
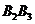 相互獨(dú)立,
相互獨(dú)立,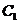
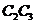 相互獨(dú)立,
相互獨(dú)立,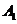 ,
,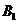 ,
,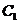 (i,j,k=1,2,3,且i,j,k互不相同)相互獨(dú)立,且P(
(i,j,k=1,2,3,且i,j,k互不相同)相互獨(dú)立,且P(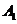 )=,P(
)=,P(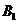 )=
)=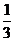 ,P(
,P(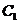 )=
)=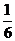
(1) 他們選擇的項(xiàng)目所屬類別互不相同的概率
P=3!P(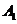
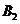
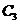 )=6P(
)=6P(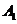 )P(
)P(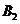 )P(
)P(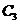 )=6
)=6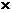
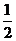
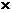
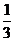
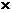
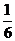 =
=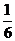
(2) 解法1 設(shè)3名工人中選擇的項(xiàng)目屬于民生工程的人數(shù)為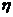 ,由己已知,
,由己已知,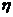 -B(3,
-B(3,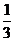 ),且
),且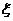 =3
=3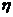 。
。
所以P(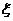 =0)=P(
=0)=P(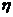 =3)=
=3)=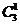
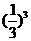 =
=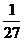 ,
,
P(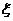 =1)=P(
=1)=P(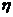 =2)=
=2)= 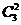
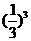
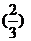 =
= 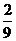


P(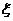 =2)=P(
=2)=P(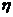 =1)=
=1)=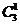
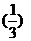
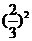 =
=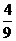
P(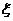 =3)=P(
=3)=P(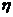 =0)=
=0)= 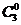
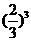 =
= 
故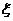 的分布是
的分布是
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
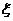 的數(shù)學(xué)期望E
的數(shù)學(xué)期望E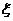 =0
=0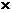
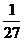 +1
+1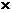
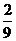 +2
+2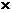
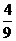 +3
+3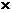
 =2
=2
解法2 第i名工人選擇的項(xiàng)目屬于基礎(chǔ)工程或產(chǎn)業(yè)工程分別為事件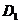 ,
,
i=1,2,3 ,由此已知,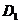 ·D,
·D,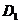 相互獨(dú)立,且
相互獨(dú)立,且
P(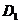 )-(
)-(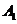 ,
,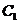 )= P(
)= P(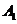 )+P(
)+P(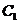 )=
)=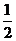 +
+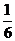 =
=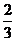
所以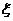 --
--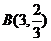 ,既
,既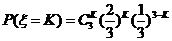 ,
,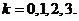

故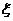 的分布列是
的分布列是
|
| 1 | 2 | 3 |
|
|
|
|
|
18.(本小題滿分12分)
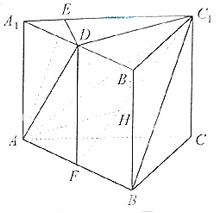
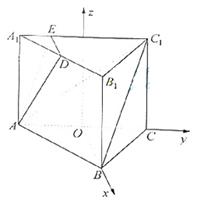
如圖4,在正三棱柱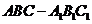 中,
中,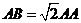
D是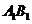 的中點(diǎn),點(diǎn)E在
的中點(diǎn),點(diǎn)E在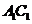 上,且
上,且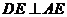 。
。
(I) 證明平面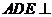 平面
平面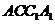
(II) 求直線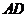 和平面
和平面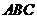 所成角的正弦值。
所成角的正弦值。
解 (I) 如圖所示,由正三棱柱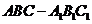 的性質(zhì)知
的性質(zhì)知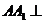 平面
平面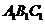
又DE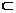 平面A
平面A B
B C
C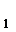 ,所以DE
,所以DE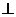 AA
AA .
.
而DE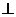 AE。AA
AE。AA
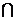 AE=A 所以DE
AE=A 所以DE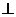 平面AC C
平面AC C A
A ,又DE
,又DE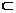 平面ADE,故平面ADE
平面ADE,故平面ADE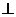 平面AC C
平面AC C A
A 。
。
(2)解法1 如圖所示,設(shè)F使AB的中點(diǎn),連接DF、DC、CF,由正三棱柱ABC- A B
B C
C 的性質(zhì)及D是A
的性質(zhì)及D是A B的中點(diǎn)知A
B的中點(diǎn)知A B
B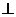 C
C D, A
D, A B
B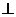 DF
DF 
又C D
D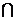 DF=D,所以A
DF=D,所以A B
B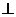 平面C
平面C DF,
DF,
而AB∥A B,所以
B,所以
AB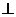 平面C
平面C DF,又AB
DF,又AB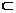 平面ABC,故
平面ABC,故
平面AB C
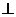 平面C
平面C DF。
DF。
過(guò)點(diǎn)D做DH垂直C F于點(diǎn)H,則DH
F于點(diǎn)H,則DH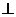 平面AB C
平面AB C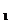 。
。
連接AH,則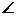 HAD是AD和平面ABC
HAD是AD和平面ABC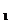 所成的角。
所成的角。
由已知AB=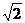 A A
A A ,不妨設(shè)A A
,不妨設(shè)A A =
=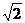 ,則AB=2,DF=
,則AB=2,DF=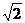 ,D C
,D C =
=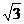 ,
,
C F=
F=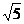 ,AD=
,AD=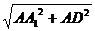 =
=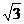 ,DH=
,DH=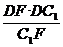 =
=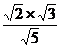 —
—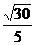 ,
,
所以 sin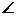 HAD=
HAD=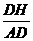 =
=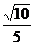 。
。
即直線AD和平面AB C 所成角的正弦值為
所成角的正弦值為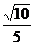 。
。
解法2 如圖所示,設(shè)O使AC的中點(diǎn),以O(shè)為原點(diǎn)建立空間直角坐標(biāo)系,不妨設(shè)
A A =
=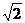 ,則AB=2,相關(guān)各點(diǎn)的坐標(biāo)分別是
,則AB=2,相關(guān)各點(diǎn)的坐標(biāo)分別是
A(0,-1,0), B(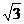 ,0,0), C
,0,0), C (0,1,
(0,1,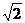 ), D(
), D(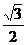 ,-
,-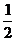 ,
,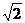 )。
)。
易知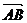 =(
=(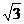 ,1,0),
,1,0), 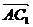 =(0,2,
=(0,2,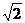 ),
), 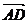 =(
=(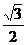 ,-
,-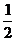 ,
,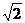 )
)

設(shè)平面ABC 的法向量為n=(x,y,z),則有
的法向量為n=(x,y,z),則有
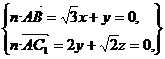
解得x=-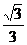 y, z=-
y, z=-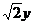 ,
,
故可取n=(1,-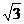 ,
,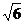 )。
)。
所以,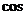 (n·
(n·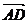 )=
)=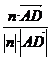 =
=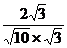 =
=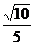 。
。
由此即知,直線AD和平面AB C 所成角的正弦值為
所成角的正弦值為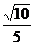 。
。