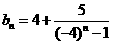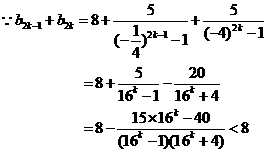(19題)本小題主要考查平面與平面垂直、直線與平面垂直、直線與平面平行、二面角等基礎(chǔ)知識(shí),考查空間想象能力、邏輯推理能力,考查應(yīng)用向量知識(shí)解決數(shù)學(xué)問題的能力。
解法一:
(Ⅰ)因?yàn)槠矫?img onmouseover='upNext(this)' title="1410503500752605.gif" src="http://pic.kekenet.com/2014/0912/1410503500752605.gif" border="0"/>
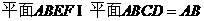
所以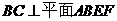
因?yàn)?img onmouseover='upNext(this)' title="1410503500588935.gif" src="http://pic.kekenet.com/2014/0912/1410503500588935.gif" border="0"/>為等腰直角三角形,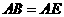 ,
,
所以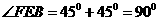
即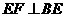
因?yàn)?img onmouseover='upNext(this)' title="1410503502296791.gif" src="http://pic.kekenet.com/2014/0912/1410503502296791.gif" border="0"/>,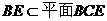
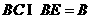 ,
,
所以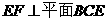
(Ⅱ)取BE的中點(diǎn)N,連結(jié)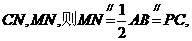
所以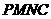 為平行四邊形,所以
為平行四邊形,所以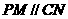
因?yàn)?img onmouseover='upNext(this)' title="1410503503527055.gif" src="http://pic.kekenet.com/2014/0912/1410503503527055.gif" border="0"/>在平面 內(nèi),
內(nèi),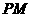 不在平面
不在平面 內(nèi),
內(nèi),
所以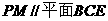
(Ⅲ)由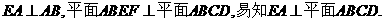
作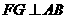 交
交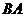 的延長線與
的延長線與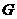 則,
則,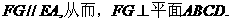
作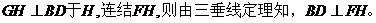
因此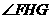 為二面角
為二面角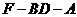 的平面角
的平面角
因此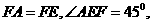
所以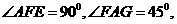
設(shè)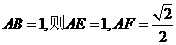
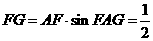
在Rt△BGH中∠GBH=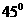 ,BG=AB+AG=1+
,BG=AB+AG=1+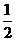 =
=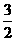 。
。
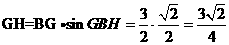
在Rt△FGH中,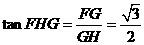
故二面角F-BD-A的大小為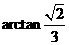 ………………….12分
………………….12分
解法二:
(Ⅰ)因?yàn)椤鰽BE為等腰直角三角形,AB=AE,
所以AE⊥AB,
又因?yàn)槠矫鍭BEF⊥平面ABCD,AE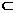 平面ABEF
平面ABEF
平面ABEF  平面ABCD= AB
平面ABCD= AB
所以AE⊥平面ABCD
所以AE⊥AD
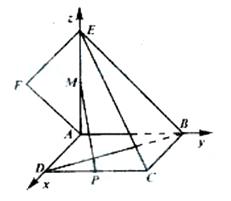
因此,AD,AB,AE兩兩垂直,建立如圖所示的直角坐
標(biāo)系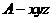 .
.
設(shè)AB=1,則AE=1,B(0,1,0),D(1,0,0),
E(0,0,1),C(1,1,0)
因?yàn)镕A=FE,∠AEF=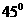 ,
,
所以∠AEF=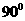 .
.
從而,F(xiàn)(0,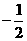 ,
,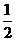 ).
).
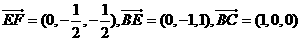 .
.
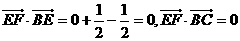
所以EF⊥BE,EF⊥BC.
因?yàn)锽E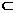 平面BCE,BC
平面BCE,BC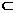 平面BCE,BC
平面BCE,BC BE=B,
BE=B,
所以EF⊥平面BCE. …………………………………4分
(Ⅱ)M(0,0,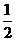 ).P(1,
).P(1, 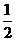 ,0).
,0).
從而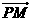 =(
=(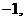
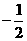 ,
,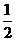 ).
).
于是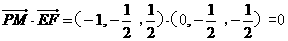
所以PM⊥FE,又EF⊥平面BCE,直線PM不在平面BCE內(nèi),
故PM∥平面BCE. ………………………8分
(Ⅲ)設(shè)平面BDF的一個(gè)法向量為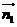 ,并設(shè)
,并設(shè)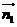 =(x,y,z)
=(x,y,z)
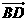 =(1,
=(1,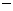 1,0),
1,0),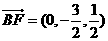
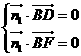 即
即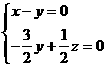
去y=1,則x=1,z=3,從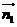 =(0,0,3)
=(0,0,3)
取平面ABD的一個(gè)法向量為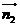 =(0,0,1)
=(0,0,1)
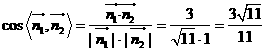
故二面角F-BD-A的大小為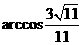 . ……………………….12分
. ……………………….12分
(20)本小題考查函數(shù)、函數(shù)極值的概念,考查應(yīng)用導(dǎo)數(shù)研究函數(shù)性質(zhì)的方法及推理和運(yùn)算能力。
解:(Ⅰ)由已知,切點(diǎn)為(2,0)故有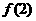 =0,即4b+c+3=0 …….①
=0,即4b+c+3=0 …….①
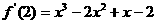 ,由已知
,由已知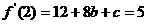 .
.
得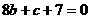 …..② 聯(lián)立①、②,解得c=1,b=
…..② 聯(lián)立①、②,解得c=1,b=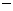 1
1
于是函數(shù)解析式為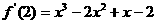 ……………..4分
……………..4分
(Ⅱ)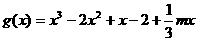
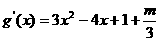 ,令
,令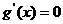
當(dāng)函數(shù)有極值時(shí),△ 0,方程
0,方程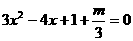 有實(shí)根,
有實(shí)根,
由△=4(1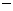 m)
m) 0,得m
0,得m  1
1
①當(dāng)m=1時(shí),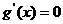 有實(shí)根
有實(shí)根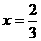 ,在
,在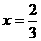 左右兩側(cè)均有
左右兩側(cè)均有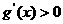 ,故
,故
函數(shù)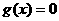 無極值。
無極值。
②m  1時(shí),
1時(shí),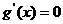 有兩個(gè)實(shí)根,
有兩個(gè)實(shí)根,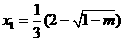 ,
,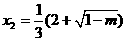 ,
,
當(dāng)x變化時(shí),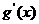 、
、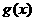 的變化情況如下表:
的變化情況如下表:
故在m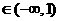 時(shí),函數(shù)
時(shí),函數(shù)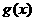 有極值:
有極值:
當(dāng)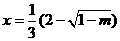 時(shí)
時(shí)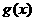 有極大值;
有極大值;
當(dāng)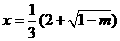 時(shí)
時(shí)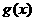 有極大值。………………………12分
有極大值。………………………12分
(21)本小題主要考查直線、橢圓、平面向量等基礎(chǔ)知識(shí),以及綜合運(yùn)用數(shù)學(xué)知識(shí)解決問題及推理運(yùn)算能力。
解:(Ⅰ)由條件有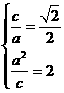 解得a=
解得a=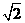 ,c=1
,c=1 

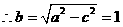
所以,所求橢圓的方程為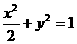 ………………….4分
………………….4分
(Ⅱ)由(Ⅰ)知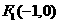 、
、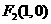


若直線L的斜率不存在,則直線L的方程為x= —1,
將x= —1代入橢圓方程的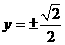
不妨設(shè)M 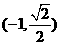 、N
、N 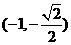
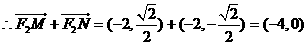
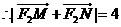 ,與題設(shè)矛盾。
,與題設(shè)矛盾。 

∴直線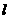 的斜率存在
的斜率存在
設(shè)直線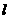 的斜率為
的斜率為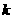 ,則直線
,則直線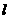 的方程為
的方程為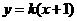
設(shè)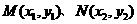
聯(lián)立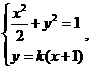 消
消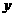 得
得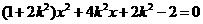
由根與系數(shù)的關(guān)系知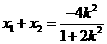 ,從而
,從而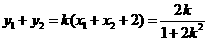
又∵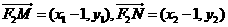 ,
, 

∴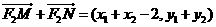
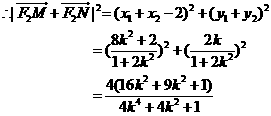
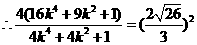


化簡(jiǎn)得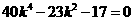
解得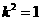 或
或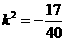 (舍)
(舍)
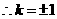
∴所求直線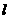 的方程為
的方程為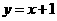 或
或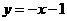
(22)本小題主要考查數(shù)列、不等式等基礎(chǔ)知識(shí),化歸思想等數(shù)學(xué)思想方法,以及推理論證、分析與解決問題的能力。
解:(Ⅰ)當(dāng)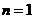 時(shí),
時(shí),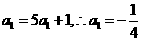
又∵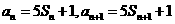
∴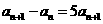 ,即
,即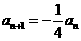
∴數(shù)列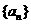 成等比數(shù)列,其首項(xiàng)
成等比數(shù)列,其首項(xiàng)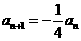


∴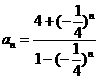
(Ⅱ)不存在正整數(shù)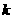 ,使得
,使得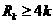 成立
成立
下證:對(duì)任意的正整數(shù)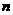 ,都有
,都有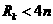 成立
成立 

由(Ⅰ)知