一、選擇題:
1.設集合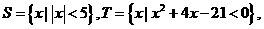 則
則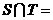
A.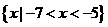 B.
B.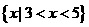 C.
C.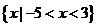 D.
D.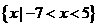
【考點定位】本小題考查解含有絕對值的不等式、一元二次不等式,考查集合的運算,基礎題。
解析:由題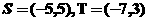 ,故選擇C。
,故選擇C。
解析2:由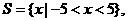
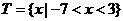 故
故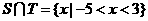 ,故選C.
,故選C.
2.已知函數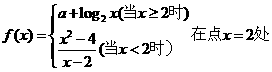 連續,則常數
連續,則常數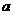 的值是
的值是
A.2 B.3 C.4 D.5
【考點定位】本小題考查函數的連續性,考查分段函數,基礎題。
解析:由題得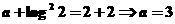 ,故選擇B。
,故選擇B。
解析2:本題考查分段函數的連續性.由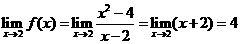 ,
,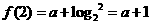 ,由函數的連續性在一點處的連續性的定義知
,由函數的連續性在一點處的連續性的定義知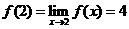 ,可得
,可得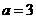 .故選B.
.故選B.
3.復數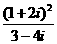 的值是
的值是
A.-1 B.1 C.-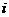 D.
D.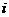
【考點定位】本小題考查復數的運算,基礎題。
解析: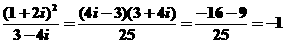 ,故選擇A。
,故選擇A。
4.已知函數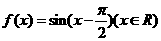 ,下面結論錯誤的是
,下面結論錯誤的是
A.函數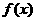 的最小正周期為
的最小正周期為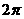 B.函數
B.函數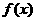 在區間
在區間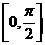 上是增函數
上是增函數
C.函數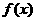 的圖像關于直線
的圖像關于直線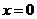 對稱 D.函數
對稱 D.函數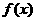 是奇函數
是奇函數
【考點定位】本小題考查誘導公式、三角函數的奇偶性、周期、單調性等,基礎題。(同文4)
解析:由函數的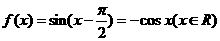 可以得到函數
可以得到函數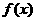 是偶函數,所以選擇D.
是偶函數,所以選擇D.
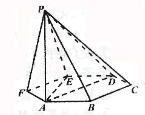
5.如圖,已知六棱錐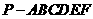 的底面是正六邊形,
的底面是正六邊形, ,則下列結論正確的是
,則下列結論正確的是
A.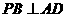
B.平面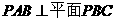
C. 直線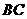 ∥平面
∥平面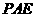
D.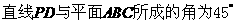
【考點定位】本小題考查空間里的線線、線面關系,基礎題。(同文6)
解:由三垂線定理,因AD與AB不相互垂直,排除A;作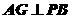 于
于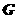 ,
,
因面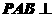 面ABCDEF,而AG在面ABCDEF上的射影在AB上,而AB與BC不相互垂直,故排除B;由
面ABCDEF,而AG在面ABCDEF上的射影在AB上,而AB與BC不相互垂直,故排除B;由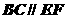 ,而EF是平面PAE的斜線,故排除C,故選擇D。
,而EF是平面PAE的斜線,故排除C,故選擇D。
解析2:設低面正六邊形邊長為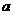 ,則
,則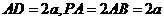 ,由
,由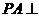 平面
平面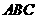 可知
可知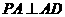 ,
,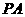 且
且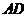 ,所以在
,所以在 中有直線
中有直線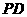 與平面
與平面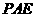 所成的角為
所成的角為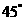 ,故應選D。
,故應選D。
6.已知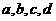 為實數,且
為實數,且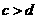 。則“
。則“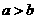 ”是“
”是“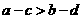 ”的
”的
A. 充分而不必要條件 B. 必要而不充分條件
C.充要條件 D. 既不充分也不必要條件
【考點定位】本小題考查不等式的性質、簡單邏輯,基礎題。(同文7)
解析: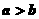 推不出
推不出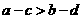 ;但
;但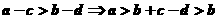 ,故選擇B。
,故選擇B。
解析2:令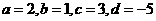 ,則
,則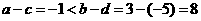 ;由
;由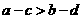 可得,
可得,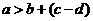 因為
因為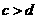 ,則
,則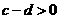 ,所以
,所以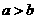 。故“
。故“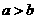 ”是“
”是“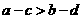 ”的必要而不充分條件。
”的必要而不充分條件。
7.已知雙曲線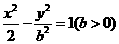 的左右焦點分別為
的左右焦點分別為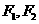 ,其一條漸近線方程為
,其一條漸近線方程為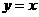 ,點
,點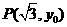 在該雙曲線上,則
在該雙曲線上,則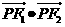 =
=
A.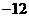 B.
B.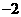 C .0 D. 4
C .0 D. 4
【考點定位】本小題考查雙曲線的漸近線方程、雙曲線的定義,基礎題。(同文8)
解析:由題知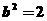 ,故
,故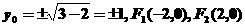 ,
,
∴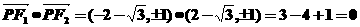 ,故選擇C。
,故選擇C。
解析2:根據雙曲線漸近線方程可求出雙曲線方程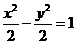 ,則左、右焦點坐標分別為
,則左、右焦點坐標分別為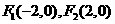 ,再將點
,再將點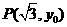 代入方程可求出
代入方程可求出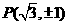 ,則可得
,則可得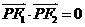 ,故選C。
,故選C。
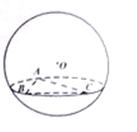
8.如圖,在半徑為3的球面上有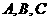 三點,
三點,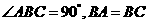 ,球心
,球心 到平面
到平面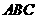 的距離是
的距離是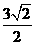 ,則
,則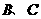 兩點的球面距離是
兩點的球面距離是
A.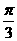 B.
B.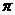 C.
C.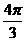 D.
D.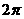
【考點定位】本小題考查球的截面圓性質、球面距,基礎題。(同文9)
解析:由知截面圓的半徑
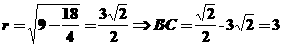 ,故
,故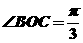 ,所以
,所以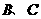 兩點的球面距離為
兩點的球面距離為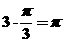 ,故選擇B。
,故選擇B。
解析2:過球心 作平面
作平面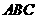 的垂線交平面與
的垂線交平面與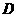 ,
,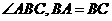 ,則
,則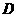 在直線
在直線 上,由于
上,由于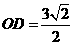 ,
,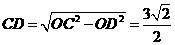 ,所以
,所以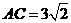 ,由
,由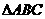 為等腰直角三角形可得
為等腰直角三角形可得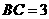 ,所以
,所以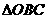 為等邊三角形,則
為等邊三角形,則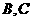 兩點的球面距離是
兩點的球面距離是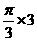 。
。
9.已知直線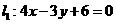 和直線
和直線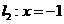 ,拋物線
,拋物線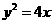 上一動點
上一動點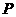 到直線
到直線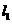 和直線
和直線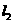 的距離之和的最小值是
的距離之和的最小值是
A.2 B.3 C.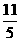 D.
D.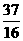
【考點定位】本小題考查拋物線的定義、點到直線的距離,綜合題。
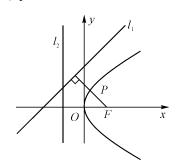
解析:直線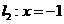 為拋物線
為拋物線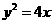 的準線,由拋物線的定義知,P到
的準線,由拋物線的定義知,P到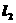 的距離等于P到拋物線的焦點
的距離等于P到拋物線的焦點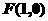 的距離,故本題化為在拋物線
的距離,故本題化為在拋物線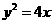 上找一個點
上找一個點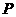 使得
使得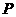 到點
到點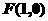 和直線
和直線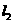 的距離之和最小,最小值為
的距離之和最小,最小值為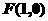 到直線
到直線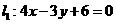 的距離,即
的距離,即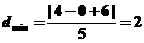 ,故選擇A。
,故選擇A。
解析2:如下圖,由題意可知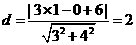
10.某企業生產甲、乙兩種產品,已知生產每噸甲產品要用A原料3噸、B原料2噸;生產每噸乙產品要用A原料1噸、B原料3噸。銷售每噸甲產品可獲得利潤5萬元,每噸乙產品可獲得利潤3萬元,該企業在一個生產周期內消耗A原料不超過13噸,B原料不超過18噸,那么該企業可獲得最大利潤是
A. 12萬元 B. 20萬元 C. 25萬元 D. 27萬元
【考點定位】本小題考查簡單的線性規劃,基礎題。(同文10)
解析:設甲、乙種兩種產品各需生產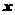 、
、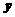 噸,可使利潤
噸,可使利潤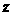 最大,故本題即
最大,故本題即
已知約束條件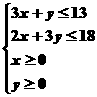 ,求目標函數
,求目標函數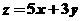 的最大值,
的最大值,
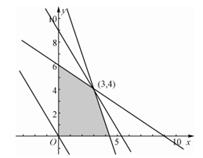
可求出最優解為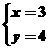 ,故
,故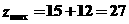 ,故選擇D。
,故選擇D。
11.3位男生和3位女生共6位同學站成一排,若男生甲不站兩端,3位女生中有且只有兩位女生相鄰,則不同排法的種數是
A. 360 B. 188 C. 216 D. 96
【考點定位】本小題考查排列綜合問題,基礎題。
解析:6位同學站成一排,3位女生中有且只有兩位女生相鄰的排法有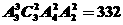 種,其中男生甲站兩端的有
種,其中男生甲站兩端的有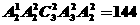 ,符合條件的排法故共有188
,符合條件的排法故共有188
解析2:由題意有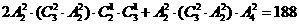 ,選B。
,選B。
12.已知函數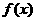 是定義在實數集
是定義在實數集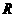 上的不恒為零的偶函數,且對任意實數
上的不恒為零的偶函數,且對任意實數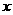 都有
都有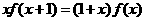 ,則
,則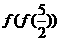 的值是
的值是
A.0 B.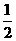 C.1 D.
C.1 D.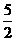
【考點定位】本小題考查求抽象函數的函數值之賦值法,綜合題。(同文12)
解析:令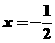 ,則
,則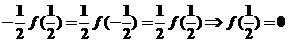 ;令
;令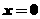 ,則
,則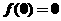
由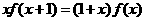 得
得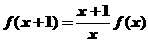 ,所以
,所以
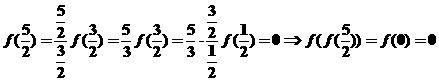 ,故選擇A。
,故選擇A。
二、填空題:本大題共4小題,每小題4分,共16分.把答案填在題中橫線上.
13.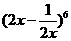 的展開式的常數項是____________(用數字作答)
的展開式的常數項是____________(用數字作答)
【考點定位】本小題考查二項式展開式的特殊項,基礎題。(同文13)
解析:由題知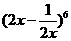 的通項為
的通項為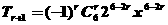 ,令
,令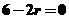 得
得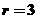 ,故常數項為
,故常數項為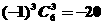 。
。
14.若⊙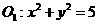 與⊙
與⊙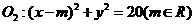 相交于A、B兩點,且兩圓在點A處的切線互相垂直,則線段AB的長度是
相交于A、B兩點,且兩圓在點A處的切線互相垂直,則線段AB的長度是
【考點定位】本小題考查圓的標準方程、兩直線的位置關系等知識,綜合題。
解析:由題知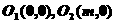 ,且
,且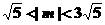 ,又
,又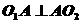 ,所以有
,所以有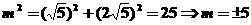 ,∴
,∴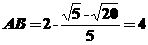 。
。
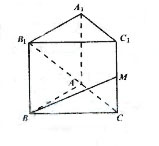
15.如圖,已知正三棱柱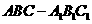 的各條棱長都相等,
的各條棱長都相等,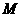 是側 棱
是側 棱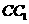 的中點,則異面直線
的中點,則異面直線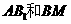 所成的角的大小是 ___________。
所成的角的大小是 ___________。
【考點定位】本小題考查異面直線的夾角,基礎題。
解析:不妨設棱長為2,選擇基向量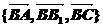 ,則
,則
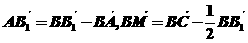
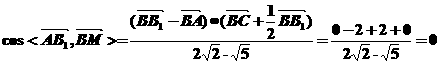 ,故填寫
,故填寫 。
。
法2:取BC中點N,連結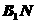 ,則
,則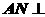 面
面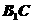 ,∴
,∴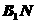 是
是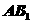 在面
在面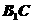 上的射影,由幾何知識知
上的射影,由幾何知識知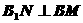 ,由三垂線定理得
,由三垂線定理得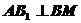 ,故填寫
,故填寫 。
。
16.設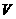 是已知平面
是已知平面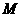 上所有向量的集合,對于映射
上所有向量的集合,對于映射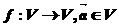 ,記
,記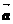 的象為
的象為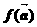 。若映射
。若映射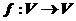 滿足:對所有
滿足:對所有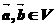 及任意實數
及任意實數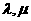 都有
都有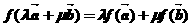 ,則
,則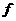 稱為平面
稱為平面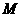 上的線性變換。現有下列命題:
上的線性變換。現有下列命題:
①設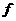 是平面
是平面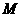 上的線性變換,則
上的線性變換,則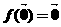
②對 設
設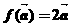 ,則
,則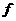 是平面
是平面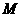 上的線性變換;
上的線性變換;
③若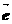 是平面
是平面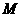 上的單位向量,對
上的單位向量,對 設
設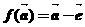 ,則
,則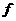 是平面
是平面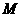 上的線性變換;
上的線性變換;
④設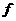 是平面
是平面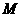 上的線性變換,
上的線性變換,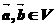 ,若
,若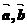 共線,則
共線,則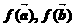 也共線。
也共線。
其中真命題是 (寫出所有真命題的序號)
【考點定位】本小題考查新定義,創新題。
解析:令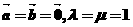 ,由題有
,由題有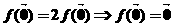 ,故①正確;
,故①正確;
由題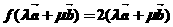 ,
,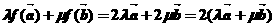 ,即
,即
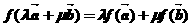 ,故②正確;
,故②正確;
由題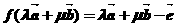 ,
,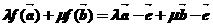 ,即
,即
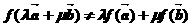 ,故③不正確;
,故③不正確;
由題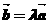 ,
,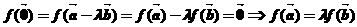 ,即
,即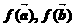 也共線,故④正確;
也共線,故④正確;