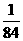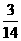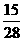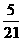三、解答題:本大題共6小題,共74分.解答應(yīng)寫出文字說明、證明過程或演算步驟.
17. (本小題滿分12分)
在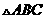 中,
中, 為銳角,角
為銳角,角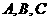 所對(duì)應(yīng)的邊分別為
所對(duì)應(yīng)的邊分別為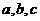 ,且
,且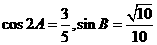
(I)求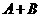 的值;
的值;

(II)若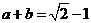 ,求
,求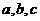 的值。
的值。
本小題主要考查同角三角函數(shù)間的關(guān)系,兩角和差的三角函數(shù)、二倍角公式、正弦定理等基礎(chǔ)知識(shí)及基本運(yùn)算能力。
解:(Ⅰ)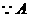 、
、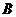 為銳角,
為銳角,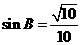 ,
,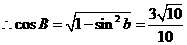
又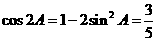 ,
,
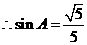 ,
,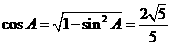 ,
,
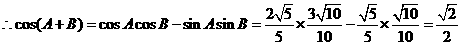
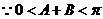
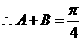 …………………………………………6分
…………………………………………6分
(Ⅱ)由(Ⅰ)知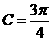 ,
,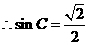 .
.
由正弦定理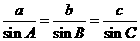 得
得
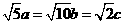 ,即
,即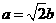 ,
,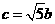


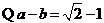 ,
,
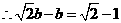 ,
,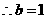
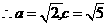 ……………………………………12分
……………………………………12分
18. (本小題滿分12分)
為振興旅游業(yè),四川省2009年面向國內(nèi)發(fā)行總量為2000萬張的熊貓優(yōu)惠卡,向省外人士發(fā)行的是熊貓金卡(簡(jiǎn)稱金卡),向省內(nèi)人士發(fā)行的是熊貓銀卡(簡(jiǎn)稱銀卡)。某旅游公司組織了一個(gè)有36名游客的旅游團(tuán)到四川名勝旅游,其中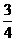 是省外游客,其余是省內(nèi)游客。在省外游客中有
是省外游客,其余是省內(nèi)游客。在省外游客中有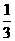 持金卡,在省內(nèi)游客中有
持金卡,在省內(nèi)游客中有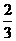 持銀卡。
持銀卡。
(I)在該團(tuán)中隨機(jī)采訪3名游客,求恰有1人持金卡且持銀卡者少于2人的概率;
(II)在該團(tuán)的省內(nèi)游客中隨機(jī)采訪3名游客,設(shè)其中持銀卡人數(shù)為隨機(jī)變量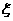 ,求
,求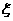 的分布列及數(shù)學(xué)期望
的分布列及數(shù)學(xué)期望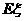 。
。
本小題主要考察相互獨(dú)立事件、互斥事件、隨機(jī)變量的分布列、數(shù)學(xué)期望等概率計(jì)算,考察運(yùn)用概率只是解決實(shí)際問題的能力。
解:(Ⅰ)由題意得,省外游客有27人,其中9人持金卡;省內(nèi)游客有9人,其中6人持銀卡。設(shè)事件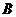 為“采訪該團(tuán)3人中,恰有1人持金卡且持銀卡者少于2人”,
為“采訪該團(tuán)3人中,恰有1人持金卡且持銀卡者少于2人”,
事件 為“采訪該團(tuán)3人中,1人持金卡,0人持銀卡”,
為“采訪該團(tuán)3人中,1人持金卡,0人持銀卡”,
事件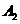 為“采訪該團(tuán)3人中,1人持金卡,1人持銀卡”。
為“采訪該團(tuán)3人中,1人持金卡,1人持銀卡”。 

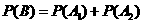
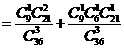
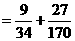
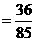
所以在該團(tuán)中隨機(jī)采訪3人,恰有1人持金卡且持銀卡者少于2人的概率是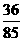 。
。
(Ⅱ)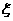 的可能取值為0,1,2,3
的可能取值為0,1,2,3
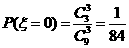 ,
, 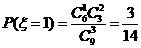
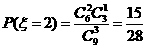 ,
,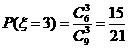 ,
,
所以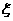 的分布列為
的分布列為
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以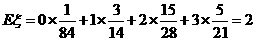 , ……………………12分
, ……………………12分
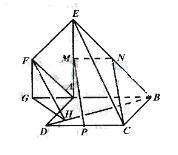
19(本小題滿分12分)如圖,正方形 所在平面與平面四邊形
所在平面與平面四邊形 所在平面互相垂直,△
所在平面互相垂直,△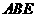 是等腰直角三角形,
是等腰直角三角形,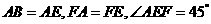
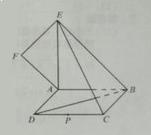
(I)求證: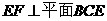 ;
;
(II)設(shè)線段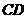 的中點(diǎn)為
的中點(diǎn)為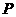 ,在直線
,在直線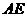 上是否存在一點(diǎn)
上是否存在一點(diǎn)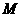 ,使得
,使得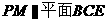 ?若存在,請(qǐng)指出點(diǎn)
?若存在,請(qǐng)指出點(diǎn)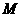 的位置,并證明你的結(jié)論;若不存在,請(qǐng)說明理由;
的位置,并證明你的結(jié)論;若不存在,請(qǐng)說明理由;
(III)求二面角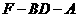 的大小。
的大小。
本小題主要考察平面與平面垂直、直線與平面垂直、直線與平面平行、二面角
等基礎(chǔ)知識(shí),考察空間想象能力、邏輯推理能力和數(shù)學(xué)探究意識(shí),考察應(yīng)用向量知識(shí)解決數(shù)學(xué)問題的能力。
解法一:
(Ⅰ)因?yàn)槠矫?img onmouseover='upNext(this)' title="1410502620888663.gif" src="http://pic.kekenet.com/2014/0912/1410502620888663.gif" alt="2009年高考數(shù)學(xué)真題附解析(四川卷+理科)" />⊥平面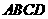 ,
,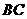
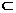 平面
平面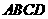 ,
,
平面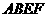
 平面
平面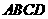
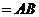 ,
,
所以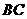 ⊥平面
⊥平面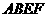
所以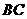 ⊥
⊥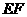 .
.
因?yàn)?img onmouseover='upNext(this)' title="1410502621509310.gif" src="http://pic.kekenet.com/2014/0912/1410502621509310.gif" alt="2009年高考數(shù)學(xué)真題附解析(四川卷+理科)" />為等腰直角三角形, 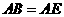 ,
,
所以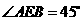
又因?yàn)?img onmouseover='upNext(this)' title="1410502622448773.gif" src="http://pic.kekenet.com/2014/0912/1410502622448773.gif" alt="2009年高考數(shù)學(xué)真題附解析(四川卷+理科)" />,
所以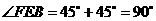 ,
,
即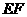 ⊥
⊥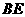
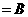 ,
,
所以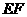 ⊥平面
⊥平面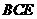 。 ……………………………………4分
。 ……………………………………4分
(Ⅱ)存在點(diǎn)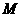 ,當(dāng)
,當(dāng)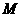 為線段AE的中點(diǎn)時(shí),PM∥平面
為線段AE的中點(diǎn)時(shí),PM∥平面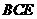
取BE的中點(diǎn)N,連接AN,MN,則MN∥=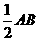 ∥=PC
∥=PC
所以PMNC為平行四邊形,所以PM∥CN
因?yàn)镃N在平面BCE內(nèi),PM不在平面BCE內(nèi),
所以PM∥平面BCE ……………………………………8分
(Ⅲ)由EA⊥AB,平面ABEF⊥平面ABCD,易知,EA⊥平面ABCD
作FG⊥AB,交BA的延長線于G,則FG∥EA。從而,F(xiàn)G⊥平面ABCD
作GH⊥BD于G,連結(jié)FH,則由三垂線定理知,BD⊥FH
因此,∠AEF為二面角F-BD-A的平面角
因?yàn)镕A=FE, ∠AEF=45°,
所以∠AFE=90°,∠FAG=45°.
設(shè)AB=1,則AE=1,AF=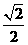 .
. 

FG=AF·sinFAG=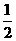
在Rt△FGH中,∠GBH=45°,BG=AB+AG=1+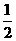 =
=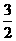 ,
,
GH=BG·sinGBH=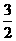 ·
·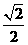 =
=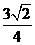
在Rt△FGH中,tanFHG=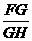 =
=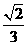
故二面角F-BD-A的大小為arctan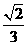 . ………………………………12分
. ………………………………12分
解法二:
(Ⅰ)因?yàn)椤鰽BE為等腰直角三角形,AB=AE,
所以AE⊥AB.
又因?yàn)槠矫鍭BEF⊥平面ABCD,AE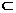 平面ABEF,
平面ABEF,
平面ABEF∩平面ABCD=AB,
所以AE⊥平面ABCD.
所以AE⊥AD.
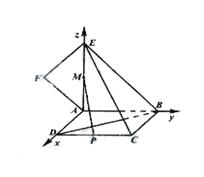
因此,AD,AB,AE兩兩垂直,以A為坐標(biāo)原點(diǎn),建立 如圖所示的直角坐標(biāo)系A(chǔ)-xyz.
設(shè)AB=1,則AE=1,B(0,1,0),D (1, 0, 0 ) ,
E ( 0, 0, 1 ), C ( 1, 1, 0 ).
因?yàn)镕A=FE, ∠AEF = 45°,
所以∠AFE= 90°.
從而,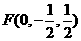 .
.
所以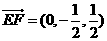 ,
,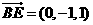 ,
,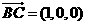 .
.
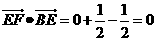 ,
,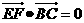 .
.
所以EF⊥BE, EF⊥BC.
因?yàn)锽E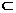 平面BCE,BC∩BE=B ,
平面BCE,BC∩BE=B ,
所以EF⊥平面BCE.
(Ⅱ) M(0,0,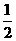 ).P(1,
).P(1,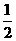 ,0).
,0).
從而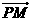 =(
=(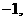
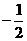 ,
,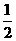 ).
).
于是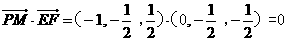
所以PM⊥FE,又EF⊥平面BCE,直線PM不在平面BCE內(nèi),
故PM∥平面BCE. ………………………………8分
(Ⅲ) 設(shè)平面BDF的一個(gè)法向量為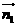 ,并設(shè)
,并設(shè)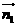 =(x,y,z)
=(x,y,z)
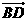 =(1,
=(1, 1,0),
1,0),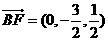
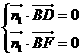 即
即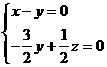
去y=1,則x=1,z=3,從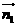 =(0,0,3)
=(0,0,3)
取平面ABD的一個(gè)法向量為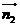 =(0,0,1)
=(0,0,1)
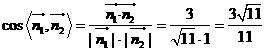
故二面角F-BD-A的大小為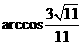 . ……………………………………12分
. ……………………………………12分