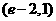一.選擇題:本大題共10小題,每小題5分,共50分.在每小題給出的四個選項中,只有一個是符合題目要求的。
1.已知集合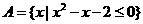 ,集合
,集合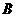 為整數集,則
為整數集,則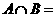
A.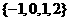 B.
B.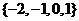 C.
C.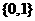 D.
D.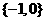
【答案】A
【解析】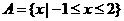 ,
,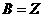 ,故
,故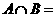
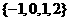
2.在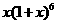 的展開式中,含
的展開式中,含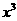 項的系數為
項的系數為
A. B.
B.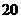 C.
C.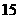 D.
D.
【答案】C
【解析】含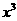 項為
項為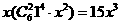
3.為了得到函數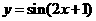 的圖象,只需把函數
的圖象,只需把函數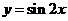 的圖象上
的圖象上
所有的點
A.向左平行移動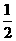 個單位長度 B.向右平行移動
個單位長度 B.向右平行移動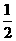 個單位長度
個單位長度
C.向左平行移動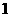 個單位長度 D.向右平行移動
個單位長度 D.向右平行移動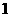 個單位長度
個單位長度
【答案】A
【解析】因為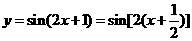 ,故可由函數
,故可由函數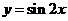 的圖象上所有的點向左平行移動
的圖象上所有的點向左平行移動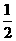 個單位長度得到
個單位長度得到
4.若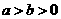 ,
,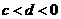 ,則一定有
,則一定有
A.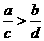 B.
B.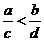 C.
C.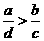 D.
D.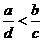
【答案】D
【解析】由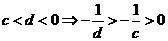 ,又
,又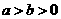 ,由不等式性質知:
,由不等式性質知: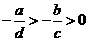 ,所以
,所以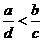
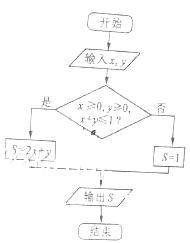
5.執行如圖1所示的程序框圖,如果輸入的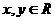 ,則輸出的
,則輸出的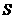 的最大值為
的最大值為
A. B.
B.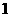 C.
C.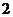 D.
D.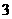
【答案】C
【解析】當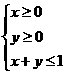 時,函數
時,函數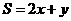 的最大值為2,否則,
的最大值為2,否則,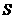 的值為1.
的值為1.
6.六個人從左至右排成一行,最左端只能排甲或乙,最右端不能拍甲,則不同的排法共有
A.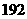 種 B.
種 B.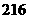 種 C.
種 C.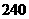 種 D.
種 D.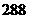 種
種
【答案】B
【解析】當最左端為甲時,不同的排法共有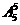 種;當最左端為乙時,不同的排法共有
種;當最左端為乙時,不同的排法共有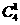
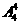 種。
種。
共有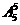 +
+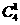
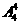
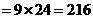 種
種
7.平面向量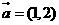 ,
,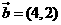 ,
,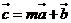 (
(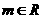 ),且
),且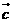 與
與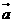 的夾角等于
的夾角等于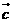 與
與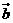 的夾角,則
的夾角,則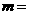
A.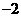 B.
B.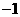 C.
C.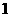 D.
D.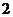
【答案】D
【解析1】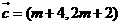
因為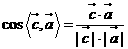 ,
,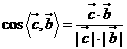 ,所以
,所以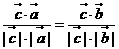 ,又
,又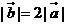
所以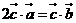 即
即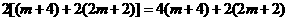
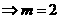
【解析2】由幾何意義知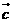 為以
為以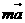 ,
,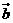 為鄰邊的菱形的對角線向量,又
為鄰邊的菱形的對角線向量,又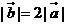 故
故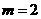
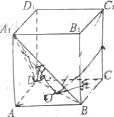
8.如圖,在正方體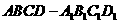 中,點
中,點 為線段
為線段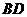 的中點。設點
的中點。設點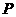 在線段
在線段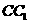 上,直線
上,直線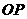 與平面
與平面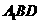 所成的角為
所成的角為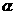 ,則
,則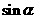 的取值范圍是
的取值范圍是
A.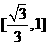 B.
B.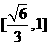 C.
C.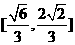 D.
D.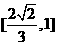
【答案】B
【解析】直線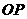 與平面
與平面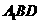 所成的角為
所成的角為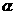 的取值范圍是
的取值范圍是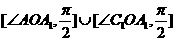 ,
,
由于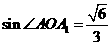 ,
,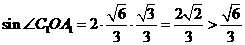 ,
,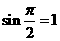 所以
所以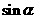 的取值范圍是
的取值范圍是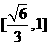
9.已知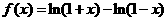 ,
,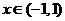 。現有下列命題:
。現有下列命題:
①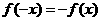 ;②
;②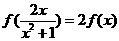 ;③
;③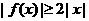 。其中的所有正確命題的序號是
。其中的所有正確命題的序號是
A.①②③ B.②③ C.①③ D.①②
【答案】C
【解析】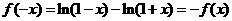 故①正確
故①正確
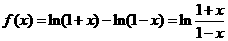
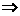
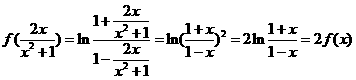
但左邊的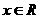 ,右邊的
,右邊的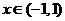 ,故②不正確
,故②不正確
當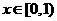 時,
時,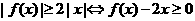
令 (
(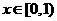 )
)
因為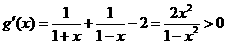 ,所以
,所以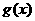 在
在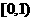 單增,
單增,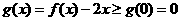
即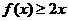 ,又
,又 與
與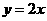 為奇函數,所以
為奇函數,所以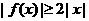 成立故③正確
成立故③正確
10.已知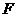 是拋物線
是拋物線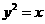 的焦點,點
的焦點,點 ,
,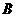 在該拋物線上且位于
在該拋物線上且位于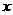 軸的兩側,
軸的兩側,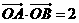 (其中
(其中 為
為
坐標原點),則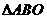 與
與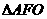 面積之和的最小值是
面積之和的最小值是
A.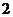 B.
B.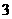 C.
C.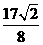 D.
D.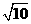
【答案】B
【解析】設直線AB的方程為: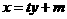 ,點
,點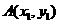 ,
,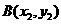 ,又
,又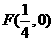 ,直線AB與
,直線AB與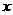 軸的交點
軸的交點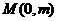 (不妨假設
(不妨假設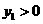 )
)
 由
由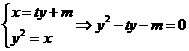 ,所以
,所以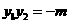
又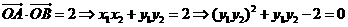
因為點 ,
,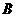 在該拋物線上且位于
在該拋物線上且位于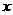 軸的兩側,所以
軸的兩側,所以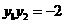 ,故
,故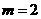
于是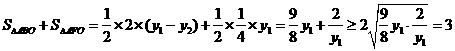
當且僅當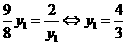 時取“
時取“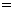 ”
”
所以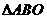 與
與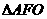 面積之和的最小值是
面積之和的最小值是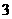
二.填空題:本大題共5小題,每小題5分,共25分。
11.復數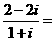 _____________。
_____________。
【答案】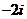
【解析】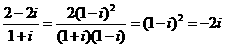
12.設 是定義在R上的周期為2的函數,當
是定義在R上的周期為2的函數,當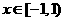 時,
時,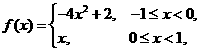 ,則
,則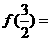 ___________。
___________。
【答案】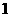
【解析】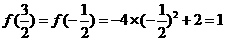
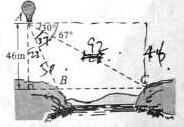
13.如圖,從氣球A上測得正前方的河流的兩岸B,C的俯角分別為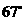 ,
, ,此時氣球的高是
,此時氣球的高是 ,則河流的寬度BC約等于___________
,則河流的寬度BC約等于___________  。(用四舍五入法將結果精確到個位。參考數據:
。(用四舍五入法將結果精確到個位。參考數據: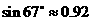 ,
,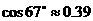 ,
,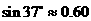 ,
,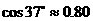 ,
,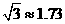 )
)
【答案】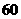
【解析】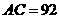 ,
,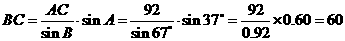
14.設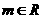 ,過定點A的動直線
,過定點A的動直線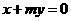 和過定點B的動直線
和過定點B的動直線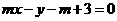 交于點
交于點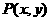 ,則
,則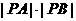 的最大值是___________。
的最大值是___________。
【答案】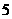
【解析】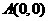 ,
,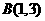 ,因為
,因為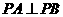 ,所以
,所以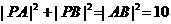 ,故
,故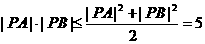 (當且僅當
(當且僅當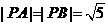 時取“
時取“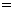 ”)
”)
15.以 表示值域為R的函數組成的集合,
表示值域為R的函數組成的集合,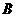 表示具有如下性質的函數
表示具有如下性質的函數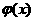 組成的集合:對于函數
組成的集合:對于函數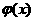 ,存在一個正數
,存在一個正數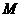 ,使得函數
,使得函數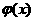 的值域包含于區間
的值域包含于區間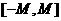 。例如,當
。例如,當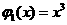 ,
,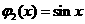 時,
時,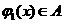 ,
,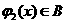 。現有如下命題:
。現有如下命題:
①設函數 的定義域為
的定義域為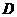 ,則“
,則“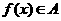 ”的充要條件是“
”的充要條件是“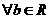 ,
,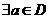 ,
, ”;
”;
②函數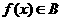 的充要條件是
的充要條件是 有最大值和最小值;
有最大值和最小值;
③若函數 ,
,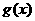 的定義域相同,且
的定義域相同,且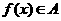 ,
,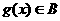 ,則
,則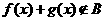 ;
;
④若函數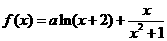 (
(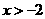 ,
,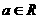 )有最大值,則
)有最大值,則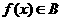 。
。
其中的真命題有___________ 。(寫出所有真命題的序號)
【答案】①③④
三.解答題:本大題共6小題,共 75分。解答須寫出文字說明,證明過程或演算步驟。
16.已知函數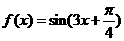 。
。
(1)求 的單調遞增區間;
的單調遞增區間;
(2)若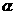 是第二象限角,
是第二象限角,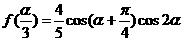 ,求
,求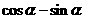 的值。
的值。
解:(1)由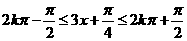
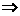
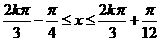
所以 的單調遞增區間為
的單調遞增區間為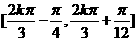 (
(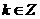 )
)
(2)由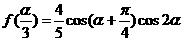
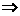
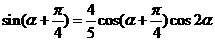
因為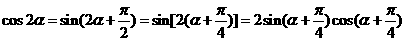
所以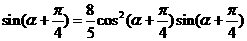
又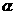 是第二象限角,所以
是第二象限角,所以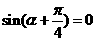 或
或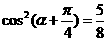
①由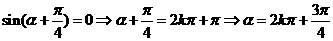 (
(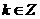 )
)
所以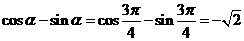
②由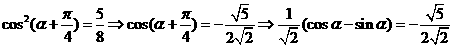
所以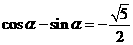
綜上,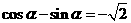 或
或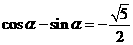
17.一款擊鼓小游戲的規則如下:每盤游戲都需要擊鼓三次,每次擊鼓要么出現一次音樂,要么不出現音樂;每盤游戲擊鼓三次后,出現一次音樂獲得10分,出現兩次音樂獲得20分,出現三次音樂獲得100分,沒有出現音樂則扣除200分(即獲得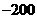 分)。設每次擊鼓出現音樂的概率為
分)。設每次擊鼓出現音樂的概率為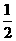 ,且各次擊鼓出現音樂相互獨立。
,且各次擊鼓出現音樂相互獨立。
(1)設每盤游戲獲得的分數為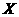 ,求
,求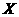 的分布列;
的分布列;
(2)玩三盤游戲,至少有一盤出現音樂的概率是多少?
(3)玩過這款游戲的許多人都發現,若干盤游戲后,與最初的分數相比,分數沒有增加反而減少了。請運用概率統計的相關知識分析分數減少的原因。
解:(1)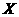 可能取值有
可能取值有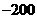 ,10,20,100
,10,20,100
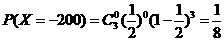 ,
,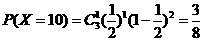 ,
,
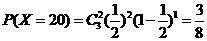 ,
,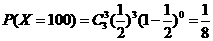
故分布列為
|
| 10 | 20 | 100 |
P |
|
|
|
|
(2)由(1)知:每盤游戲出現音樂的概率是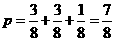
則玩三盤游戲,至少有一盤出現音樂的概率是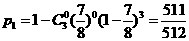
(3)由(1)知,每盤游戲獲得的分數為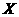 的數學期望是
的數學期望是
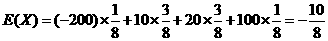 分
分
這說明每盤游戲平均得分是負分,由概率統計的相關知識可知:許多人經過若干盤游戲后,與最初的分數相比,分數沒有增加反而會減少。
18.三棱錐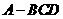 及其側視圖、俯視圖如圖所示。設
及其側視圖、俯視圖如圖所示。設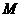 ,
,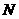 分別為線段
分別為線段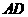 ,
,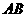 的中點,
的中點,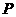 為線段
為線段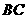 上的點,且
上的點,且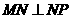 。
。
(1)證明: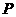 為線段
為線段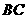 的中點;
的中點;
(2)求二面角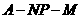 的余弦值。
的余弦值。
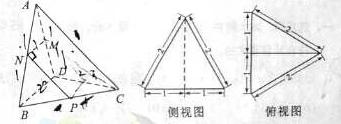
解:(1)由三棱錐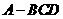 及其側視圖、俯視圖可知,在三棱錐
及其側視圖、俯視圖可知,在三棱錐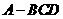 中:
中:
平面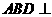 平面
平面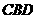 ,
,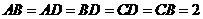
設 為
為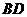 的中點,連接
的中點,連接 ,
,
于是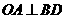 ,
,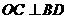 所以
所以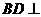 平面
平面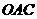
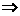
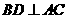
因為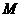 ,
,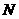 分別為線段
分別為線段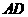 ,
,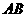 的中點,所以
的中點,所以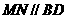 ,又
,又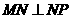 ,故
,故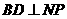
假設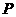 不是線段
不是線段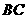 的中點,則直線
的中點,則直線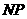 與直線
與直線 是平面
是平面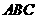 內相交直線
內相交直線
從而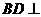 平面
平面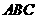 ,這與
,這與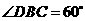 矛盾
矛盾
所以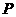 為線段
為線段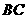 的中點
的中點
(2)以 為坐標原點,
為坐標原點,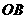 、
、 、
、 分別為
分別為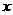 、
、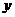 、
、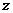 軸建立空間直角坐標系,
軸建立空間直角坐標系,
則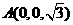 ,
,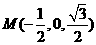 ,
,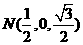 ,
,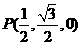
于是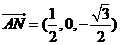 ,
,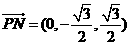 ,
,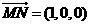
設平面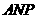 和平面
和平面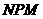 的法向量分別為
的法向量分別為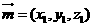 和
和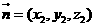
由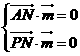
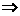
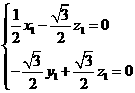 ,設
,設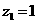 ,則
,則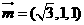
由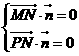
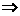
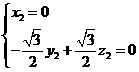 ,設
,設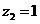 ,則
,則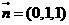
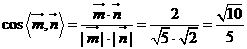
所以二面角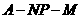 的余弦值
的余弦值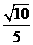
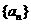 的公差為
的公差為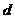 ,點
,點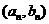 在函數
在函數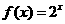 的圖象上(
的圖象上(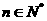 )。
)。(1)若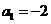 ,點
,點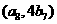 在函數
在函數 的圖象上,求數列
的圖象上,求數列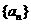 的前
的前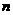 項和
項和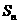 ;
;
(2)若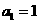 ,函數
,函數 的圖象在點
的圖象在點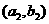 處的切線在
處的切線在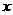 軸上的截距為
軸上的截距為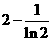 ,求數列
,求數列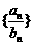 的前
的前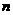 項和
項和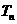 。
。
解:(1)點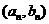 在函數
在函數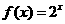 的圖象上,所以
的圖象上,所以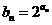 ,又等差數列
,又等差數列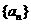 的公差為
的公差為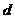
所以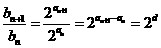
因為點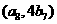 在函數
在函數 的圖象上,所以
的圖象上,所以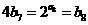 ,所以
,所以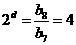
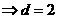
又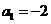 ,所以
,所以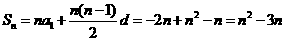
(2)由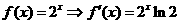
函數 的圖象在點
的圖象在點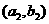 處的切線方程為
處的切線方程為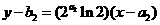
所以切線在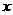 軸上的截距為
軸上的截距為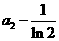 ,從而
,從而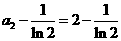 ,故
,故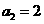
從而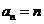 ,
,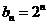 ,
,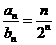
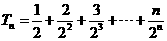
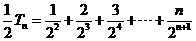
所以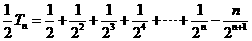
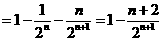
故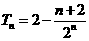
20.已知橢圓C: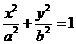 (
(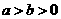 )的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形。
)的焦距為4,其短軸的兩個端點與長軸的一個端點構成正三角形。
(1)求橢圓C的標準方程;
(2)設F為橢圓C的左焦點,T為直線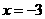 上任意一點,過F作TF的垂線交橢圓C于點P,Q。
上任意一點,過F作TF的垂線交橢圓C于點P,Q。
(i)證明:OT平分線段PQ(其中O為坐標原點);
(ii)當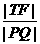 最小時,求點T的坐標。
最小時,求點T的坐標。
解:(1)依條件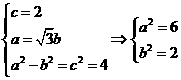
所以橢圓C的標準方程為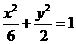
(2)設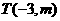 ,
,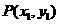 ,
,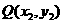 ,又設
,又設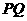 中點為
中點為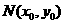
(i)因為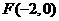 ,所以直線
,所以直線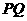 的方程為:
的方程為: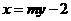
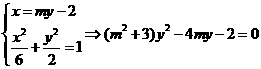
所以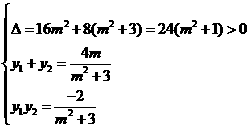
于是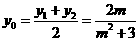 ,
,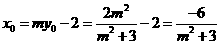
所以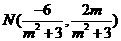 。因為
。因為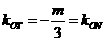
所以 ,
,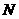 ,
,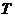 三點共線
三點共線
即OT平分線段PQ(其中O為坐標原點)
(ii)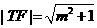 ,
,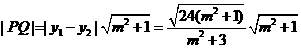
所以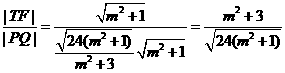 ,令
,令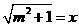 (
(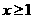 )
)
則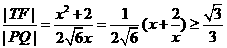 (當且僅當
(當且僅當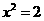 時取“
時取“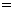 ”)
”)
所以當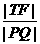 最小時,
最小時,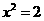 即
即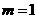 或
或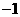 ,此時點T的坐標為
,此時點T的坐標為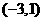 或
或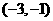
21.已知函數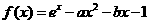 ,其中
,其中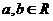 ,
,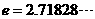 為自然對數的底數。
為自然對數的底數。
(1)設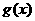 是函數
是函數 的導函數,求函數
的導函數,求函數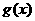 在區間
在區間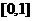 上的最小值;
上的最小值;
(2)若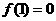 ,函數
,函數 在區間
在區間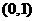 內有零點,求
內有零點,求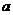 的取值范圍
的取值范圍
解:(1)因為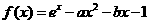 所以
所以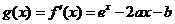 又
又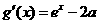
因為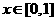 ,
,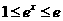 所以:
所以:
①若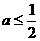 ,則
,則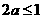 ,
,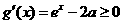 ,
,
所以函數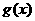 在區間
在區間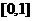 上單增,
上單增,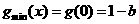
②若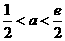 ,則
,則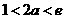 ,
,
于是當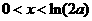 時
時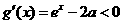 ,當
,當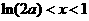 時
時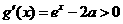 ,
,
所以函數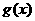 在區間
在區間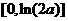 上單減,在區間
上單減,在區間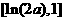 上單增,
上單增,
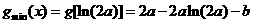
③若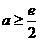 ,則
,則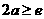 ,
,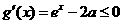
所以函數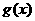 在區間
在區間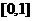 上單減,
上單減,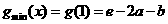
綜上: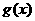 在區間
在區間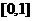 上的最小值為
上的最小值為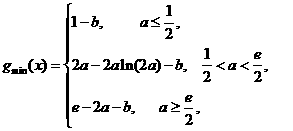
(2)由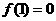
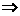
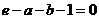
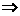
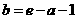 ,又
,又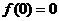
若函數 在區間
在區間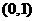 內有零點,則函數
內有零點,則函數 在區間
在區間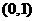 內至少有三個單調區間
內至少有三個單調區間
由(1)知當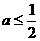 或
或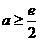 時,函數
時,函數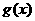 即
即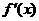 在區間
在區間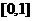 上單調,不可能滿足“函數
上單調,不可能滿足“函數 在區間
在區間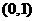 內至少有三個單調區間”這一要求。
內至少有三個單調區間”這一要求。
若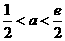 ,則
,則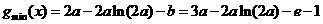
令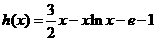 (
(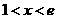 )
)
則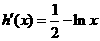 。由
。由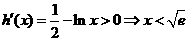
所以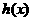 在區間
在區間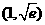 上單增,在區間
上單增,在區間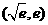 上單減
上單減
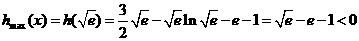 即
即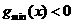 恒成立
恒成立
于是,函數 在區間
在區間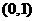 內至少有三個單調區間
內至少有三個單調區間
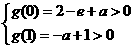
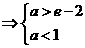
又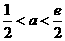 所以
所以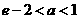
綜上,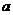 的取值范圍為
的取值范圍為