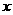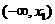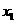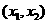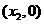20(本小題滿分12分)
已知橢圓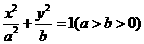 的左右焦點分別為
的左右焦點分別為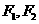 ,離心率
,離心率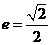 ,右準線方程為
,右準線方程為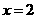 。
。
(I)求橢圓的標準方程;
(II)過點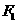 的直線
的直線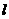 與該橢圓交于
與該橢圓交于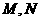 兩點,且
兩點,且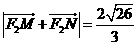 ,求直線
,求直線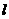 的方程。
的方程。
本小題主要考查直線、橢圓、平面向量等基礎知識,以及綜合運用數學知識解決問題及推理運算能力。
解:(Ⅰ)有條件有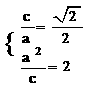 ,解得
,解得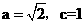 。
。


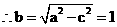 。
。
所以,所求橢圓的方程為
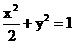 。…………………………………4分
。…………………………………4分
(Ⅱ)由(Ⅰ)知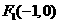 、
、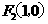 。
。
若直線l的斜率不存在,則直線l的方程為x=-1.
將x=-1代入橢圓方程得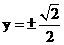 。
。
不妨設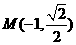 、
、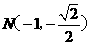 ,
,
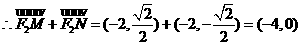 .
.
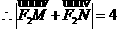 ,與題設矛盾。
,與題設矛盾。
 直線l的斜率存在。
直線l的斜率存在。
設直線l的斜率為k,則直線的方程為y=k(x+1)。
設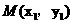 、
、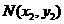 ,
,
聯立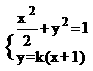 ,消y得
,消y得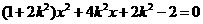 。
。
由根與系數的關系知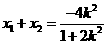 ,從而
,從而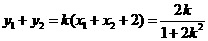 ,
,
又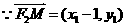 ,
,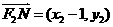 ,
,
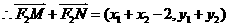 。
。
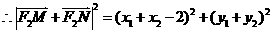
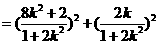
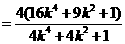
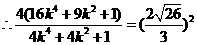 。
。
化簡得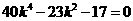
解得


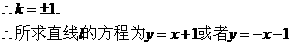
21. (本小題滿分12分)
已知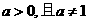 函數
函數 。
。
(I)求函數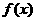 的定義域,并判斷
的定義域,并判斷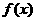 的單調性;
的單調性;
(II)若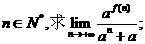
(III)當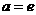 (
(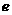 為自然對數的底數)時,設
為自然對數的底數)時,設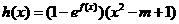 ,若函數
,若函數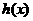 的極值存在,求實數
的極值存在,求實數 的取值范圍以及函數
的取值范圍以及函數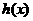 的極值。
的極值。
本小題主要考查函數、數列的極限、導數應用等基礎知識、考查分類整合思想、推理和運算能力。
解:(Ⅰ)由題意知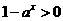
當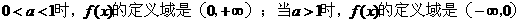
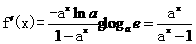
當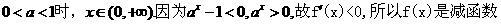
當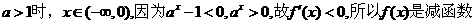 ….(4分)
….(4分)
(Ⅱ)因為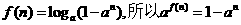
由函數定義域知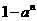 >0,因為n是正整數,故0
>0,因為n是正整數,故0
所以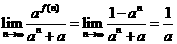
(Ⅲ)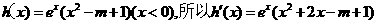
令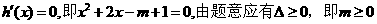
① 當m=0時,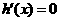 有實根
有實根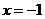 ,在
,在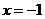 點左右兩側均有
點左右兩側均有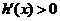 故無極值
故無極值
② 當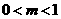 時,
時,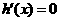 有兩個實根
有兩個實根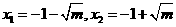
當x變化時,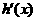 、
、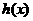 的變化情況如下表所示:
的變化情況如下表所示:
|
|
|
|
|
|
| + | 0 | - | 0 | + |
| ↗ | 極大值 | ↘ | 極小值 | ↗ |
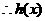 的極大值為
的極大值為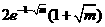 ,
,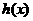 的極小值為
的極小值為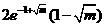
③ 當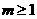 時,
時,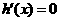 在定義域內有一個實根,
在定義域內有一個實根,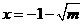
同上可得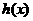 的極大值為
的極大值為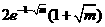
綜上所述,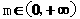 時,函數
時,函數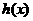 有極值;
有極值;
當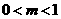 時
時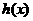 的極大值為
的極大值為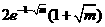 ,
,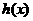 的極小值為
的極小值為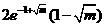
當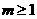 時,
時,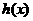 的極大值為
的極大值為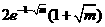


22. (本小題滿分14分)
設數列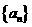 的前
的前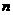 項和為
項和為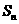 ,對任意的正整數
,對任意的正整數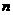 ,都有
,都有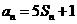 成立,記
成立,記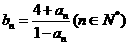 。
。
(I)求數列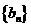 的通項公式;
的通項公式;
(II)記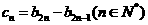 ,設數列
,設數列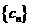 的前
的前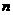 項和為
項和為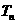 ,求證:對任意正整數
,求證:對任意正整數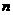 都有
都有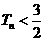 ;
;
(III)設數列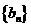 的前
的前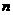 項和為
項和為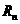 。已知正實數
。已知正實數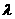 滿足:對任意正整數
滿足:對任意正整數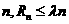 恒成立,求
恒成立,求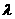 的最小值。
的最小值。
本小題主要考查數列、不等式等基礎知識、考查化歸思想、分類整合思想,以及推理論證、分析與解決問題的能力。
解:(Ⅰ)當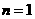 時,
時,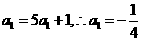
又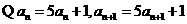
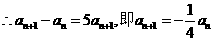
 數列
數列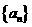 成等比數列,其首項
成等比數列,其首項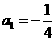 ,公比是
,公比是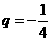
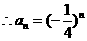
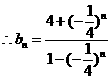 ……………………………………..3分
……………………………………..3分
(Ⅱ)由(Ⅰ)知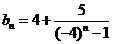
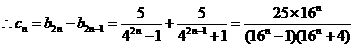
=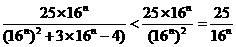
又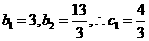
當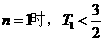
當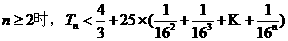
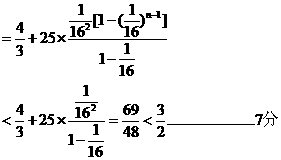


(Ⅲ)由(Ⅰ)知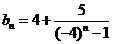
一方面,已知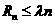 恒成立,取n為大于1的奇數時,設
恒成立,取n為大于1的奇數時,設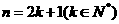
則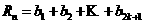
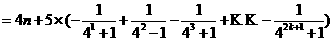
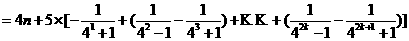
>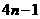
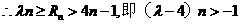 對一切大于1的奇數n恒成立
對一切大于1的奇數n恒成立
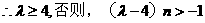 只對滿足
只對滿足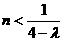 的正奇數n成立,矛盾。
的正奇數n成立,矛盾。
另一方面,當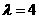 時,對一切的正整數n都有
時,對一切的正整數n都有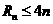
事實上,對任意的正整數k,有
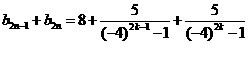
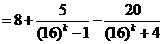
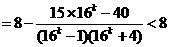
 當n為偶數時,設
當n為偶數時,設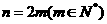
則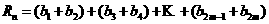
<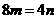


當n為奇數時,設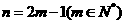
則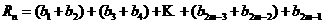
<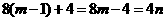
 對一切的正整數n,都有
對一切的正整數n,都有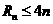
綜上所述,正實數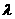 的最小值為4………………………….14分
的最小值為4………………………….14分