21.(1)雙曲線C的漸近線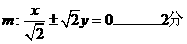
 直線l的方程
直線l的方程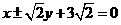 ………………..6分
………………..6分
直線l與m的距離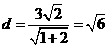 ……….8分
……….8分
(2)設過原點且平行與l的直線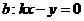
則直線l與b的距離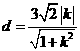
當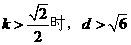
又雙曲線C的漸近線為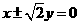
 雙曲線C的右支在直線b的右下方,
雙曲線C的右支在直線b的右下方,
 雙曲線
雙曲線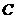 右支上的任意點到直線
右支上的任意點到直線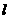 的距離為
的距離為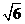 。
。
故在雙曲線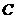 的右支上不存在點
的右支上不存在點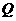 ,使之到直線
,使之到直線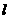 的距離為
的距離為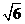 。
。
[ 證法二] 雙曲線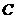 的右支上存在點
的右支上存在點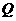
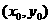 到直線
到直線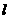 的距離為
的距離為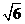 ,
,
則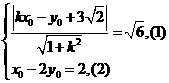
由(1)得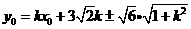 ,
,
設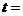
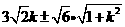
當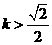 ,
,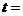
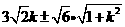
 0………………………………..13分
0………………………………..13分
將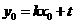 代入(2)得
代入(2)得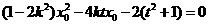 (*)
(*)
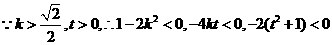
 方程(*)不存在正根,即假設不成立
方程(*)不存在正根,即假設不成立
故在雙曲線C的右支上不存在Q,使之到直線l 的距離為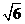 …………….16分
…………….16分
22(1)解,函數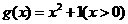 的反函數是
的反函數是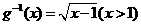
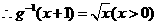
而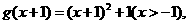 其反函數為
其反函數為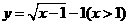
故函數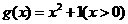 不滿足“1和性質”
不滿足“1和性質”
(2)設函數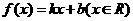 滿足“2和性質”,
滿足“2和性質”,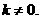
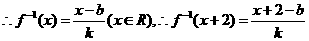 …….6分
…….6分
而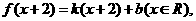 得反函數
得反函數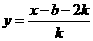 ………….8分
………….8分
由“2和性質”定義可知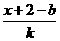 =
=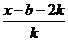 對
對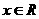 恒成立
恒成立
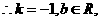 即所求一次函數為
即所求一次函數為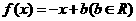 ………..10分
………..10分
(3)設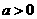 ,
,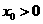 ,且點
,且點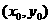 在
在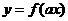 圖像上,則
圖像上,則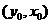 在函數
在函數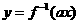 圖象上,
圖象上,
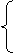 故
故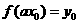 ,可得
,可得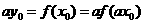 , ......12分
, ......12分
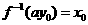 ,
,
令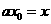 ,則
,則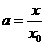 。
。
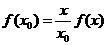 ,即
,即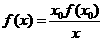 。 ......14分
。 ......14分
綜上所述,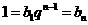
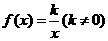 ,此時
,此時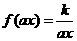 ,其反函數就是
,其反函數就是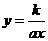 ,
,
而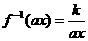 ,故
,故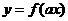 與
與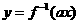 互為反函數 。 ......16分
互為反函數 。 ......16分
23.[解法一](1)由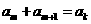 ,得
,得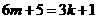 , ......2分
, ......2分
整理后,可得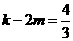 ,
,
 、
、
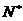 ,
,
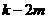 為整數,
為整數,
 不存在
不存在 、
、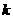
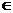
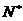 ,使等式成立。 ......5分
,使等式成立。 ......5分
(2)若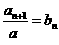 ,即
,即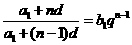 , (*)
, (*)
(ⅰ)若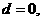 則
則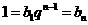 。
。
當{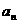 }為非零常數列,{
}為非零常數列,{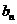 }為恒等于1的常數列,滿足要求。 ......7分
}為恒等于1的常數列,滿足要求。 ......7分
(ⅱ)若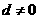 ,(*)式等號左邊取極限得
,(*)式等號左邊取極限得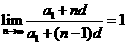 ,(*)式等號右邊的極限只有當
,(*)式等號右邊的極限只有當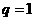 時,才能等于1。此時等號左邊是常數,
時,才能等于1。此時等號左邊是常數,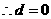 ,矛盾。
,矛盾。
綜上所述,只有當{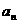 }為非零常數列,{
}為非零常數列,{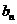 }為恒等于1的常數列,滿足要求。......10分
}為恒等于1的常數列,滿足要求。......10分
【解法二】設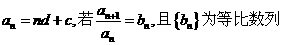
則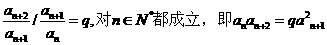
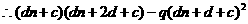
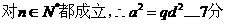
(i)若d=0,則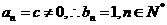
(ii)若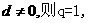
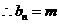 (常數)即
(常數)即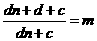 ,則d=0,矛盾
,則d=0,矛盾
綜上所述,有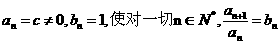 , 10分
, 10分
(3)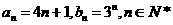
設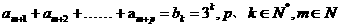 .
.
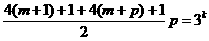 ,
,
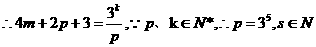 . 13分
. 13分
取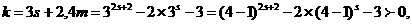 15分
15分
由二項展開式可得正整數M1、M2,使得(4-1)2s+2=4M1+1,
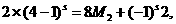
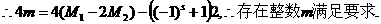
故當且僅當p=3s,s N時,命題成立.
N時,命題成立.
說明:第(3)題若學生從以下角度解題,可分別得部分分(即分步得分)
若p為偶數,則am+1+am+2+……+am+p為偶數,但3k為奇數
故此等式不成立,所以,p一定為奇數。
當p=1時,則am+1=bk,即4m+5=3k,
而3k=(4-1)k
=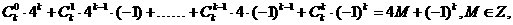
當k為偶數時,存在m,使4m+5=3k成立 1分
當p=3時,則am+1+am+2+am+3=bk,即3am+2-bk,
也即3(4m+9)=3k,所以4m+9=3k-1,4(m+1)+5=3k-1
由已證可知,當k-1為偶數即k為奇數時,存在m, 4m+9=3k成立 2分
當p=5時,則am+1+am+2+……+am+5=bk,即5am+3=bk
也即5(4m+13)=3k,而3k不是5的倍數,所以,當p=5時,所要求的m不存在
故不是所有奇數都成立. 2分











