一、填空題
1.計算: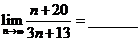
【解答】根據極限運算法則,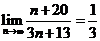 .
.
2.設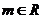 ,
,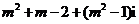 是純虛數,其中i是虛數單位,則
是純虛數,其中i是虛數單位,則
【解答】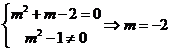 .
.
3.若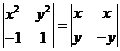 ,則
,則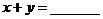
【解答】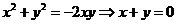 .
.
4.已知△ABC的內角A、B、C所對應邊分別為a、b、c,若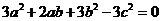 ,則角C的大小是_______________(結果用反三角函數值表示)
,則角C的大小是_______________(結果用反三角函數值表示)
【解答】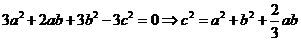 ,故
,故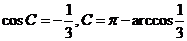 .
.
5.設常數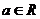 ,若
,若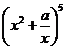 的二項展開式中
的二項展開式中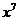 項的系數為
項的系數為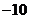 ,則
,則
【解答】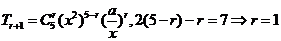 ,故
,故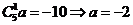 .
.
6.方程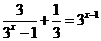 的實數解為________
的實數解為________
【解答】原方程整理后變為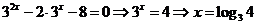 .
.
7.在極坐標系中,曲線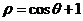 與
與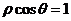 的公共點到極點的距離為__________
的公共點到極點的距離為__________
【解答】聯立方程組得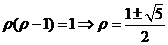 ,又
,又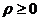 ,故所求為
,故所求為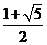 .
.
8.盒子中裝有編號為1,2,3,4,5,6,7,8,9的九個球,從中任意取出兩個,則這兩個球的編號之積為偶數的概率是___________(結果用最簡分數表示)
【解答】9個數5個奇數,4個偶數,根據題意所求概率為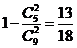 .
.
9.設AB是橢圓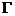 的長軸,點C在
的長軸,點C在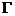 上,且
上,且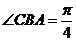 ,若AB=4,
,若AB=4,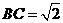 ,則
,則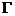 的兩個焦點之間的距離為________
的兩個焦點之間的距離為________
【解答】不妨設橢圓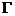 的標準方程為
的標準方程為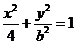 ,于是可算得
,于是可算得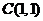 ,得
,得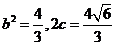 .
.
10.設非零常數d是等差數列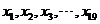 的公差,隨機變量
的公差,隨機變量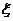 等可能地取值
等可能地取值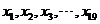 ,則方差
,則方差
【解答】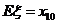 ,
,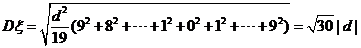 .
.
11.若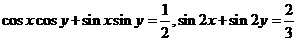 ,則
,則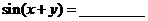
【解答】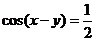 ,
,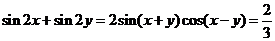 ,故
,故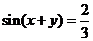 .
.
12.設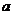 為實常數,
為實常數,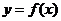 是定義在R上的奇函數,當
是定義在R上的奇函數,當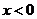 時,
時,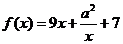 ,若
,若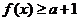 對一切
對一切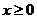 成立,則
成立,則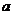 的取值范圍為________
的取值范圍為________
【解答】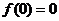 ,故
,故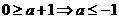 ;當
;當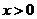 時,
時,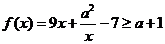
即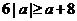 ,又
,又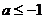 ,故
,故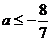 .
.
13.在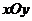 平面上,將兩個半圓弧
平面上,將兩個半圓弧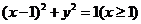 和
和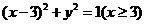 、兩條直線
、兩條直線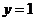 和
和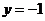 圍成的封閉圖形記為D,如圖中陰影部分.記D繞y軸旋轉一周而成的幾何體為
圍成的封閉圖形記為D,如圖中陰影部分.記D繞y軸旋轉一周而成的幾何體為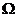 ,過
,過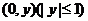 作
作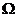 的水平截面,所得截面面積為
的水平截面,所得截面面積為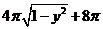 ,試利用祖暅原理、一個平放的圓柱和一個長方體,得出
,試利用祖暅原理、一個平放的圓柱和一個長方體,得出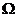 的體積值為__________
的體積值為__________

【解答】根據提示,一個半徑為1,高為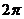 的圓柱平放,一個高為2,底面面積
的圓柱平放,一個高為2,底面面積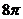 的長方體,這兩個幾何體與
的長方體,這兩個幾何體與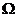 放在一起,根據祖暅原理,每個平行水平面的截面面積都相等,故它們的體積相等,即
放在一起,根據祖暅原理,每個平行水平面的截面面積都相等,故它們的體積相等,即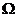 的體積值為
的體積值為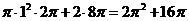 .
.
14.對區間I上有定義的函數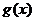 ,記
,記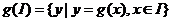 ,已知定義域為
,已知定義域為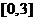 的函數
的函數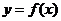 有反函數
有反函數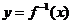 ,且
,且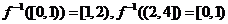 ,若方程
,若方程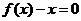 有解
有解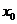 ,則
,則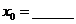
【解答】根據反函數定義,當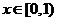 時,
時,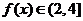 ;
;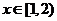 時,
時,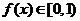 ,而
,而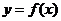 的定義域為
的定義域為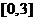 ,故當
,故當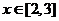 時,
時,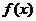 的取值應在集合
的取值應在集合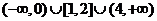 ,故若
,故若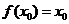 ,只有
,只有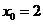 .
.











