一.填空題(本大題滿分56分)本大題共有14題,考生應在答題紙相應編號的空格內直接填寫結果,每個空格填對得4分,否則一律得零分。
1.函數f(x)=x3+1的反函數f-1(x)=_____________.
1.【答案】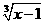
【解析】由y=x3+1,得x=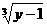 ,將y改成x,x改成y可得答案。
,將y改成x,x改成y可得答案。
2.已知集體A={x|x≤1},B={x|≥a},且A∪B=R,
則實數a的取值范圍是__________________.
2.【答案】a≤1
【解析】因為A∪B=R,畫數軸可知,實數a必須在點1上或在1的左邊,所以,有a≤1。
3. 若行列式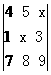 中,元素4的代數余子式大于0,則x滿足的條件是__________________.
中,元素4的代數余子式大于0,則x滿足的條件是__________________.
3.【答案】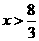
【解析】依題意,得: (-1)2×(9x-24)>0,解得: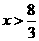
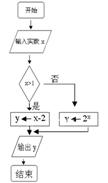
4.某算法的程序框如右圖所示,則輸出量y與輸入量x滿足的關系式是________________.
4.【答案】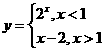
【解析】當x>1時,有y=x-2,當x<1時有y=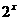 ,所以,有分段函數。
,所以,有分段函數。
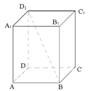
5.如圖,若正四棱柱ABCD—A1B1C1D1的底面邊長為2,高為4,則異面直線BD1與AD所成角的大小是___________________ (結果用反三角函數值表示).
5.【答案】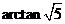
【解析】因為AD∥A1D1,異面直線BD1與AD所成角就是BD1與A1D1所在角,即∠A1D1B,
由勾股定理,得A1B=2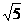 ,tan∠A1D1B=
,tan∠A1D1B=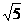 ,所以,∠A1D1B=
,所以,∠A1D1B=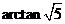 。
。
6.若球O1、O2表示面積之比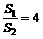 ,則它們的半徑之比
,則它們的半徑之比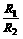 =_____________.
=_____________. 
6.【答案】2
【解析】由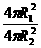 =4,得
=4,得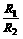 =2。
=2。
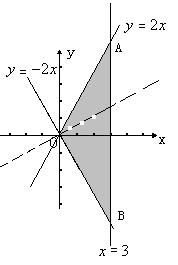
7.已知實數x、y滿足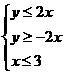 則目標函數z=x-2y的最小值是___________.
則目標函數z=x-2y的最小值是___________.
7.【答案】-9
【解析】畫出滿足不等式組的可行域如右圖,目標函數化為: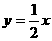 -z,畫直線
-z,畫直線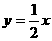 及其平行線,當此直線經過點A時,-z的值最大,z的值最小,A點坐標為(3,6),所以,z的最小值為:3-2×6=-9。
及其平行線,當此直線經過點A時,-z的值最大,z的值最小,A點坐標為(3,6),所以,z的最小值為:3-2×6=-9。
8.若等腰直角三角形的直角邊長為2,則以一直角邊所在的直線為軸旋轉一周所成的幾何體體積是________。
8.【答案】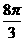
【解析】幾何體為圓錐,圓錐的底面半徑為2,高也為2,體積V=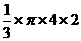 =
=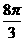
9.過點A(1,0)作傾斜角為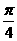 的直線,與拋物線
的直線,與拋物線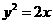 交于
交于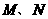 兩點,則
兩點,則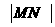 = ________。
= ________。
9.【答案】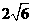
【解析】直線方程為y=x-1,代入拋物線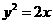 ,得:x2-4x+1=0,
,得:x2-4x+1=0,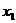 +
+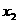 =4,
=4,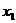
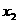 =1,則
=1,則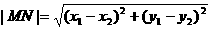 =
=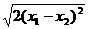 =
=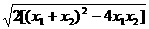 =
=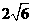
10.函數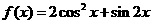 的最小值是 ________。
的最小值是 ________。
10.【答案】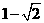
【解析】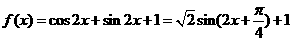 ,所以最小值為:
,所以最小值為: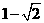
11.若某學校要從5名男生和2名女生中選出3人作為上海世博會的志愿者,則選出的志愿者中男女生均不少于1名的概率是________(結果用最簡分數表示)。
11.【答案】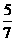
【解析】因為只有2名女生,所以選出3人中至少有一名男生,當選出的學生全是男生時有: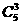 ,概率為:________:
,概率為:________: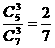 ,所以,均不少于1名的概率為:1-
,所以,均不少于1名的概率為:1-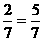 。
。
12.已知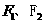 是橢圓
是橢圓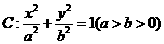 的兩個焦點,
的兩個焦點,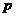 為橢圓
為橢圓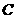 上的一點,且
上的一點,且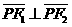 。若
。若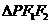 的面積為9,則
的面積為9,則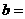 ________.
________.
12.【答案】3
【解析】依題意,有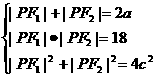 ,可得4c2+36=4a2,即a2-c2=9,故有b=3。
,可得4c2+36=4a2,即a2-c2=9,故有b=3。
13.已知函數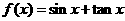 。項數為27的等差數列
。項數為27的等差數列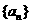 滿足
滿足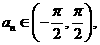 且公差
且公差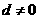 ,若
,若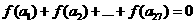 ,則當k=________時,
,則當k=________時,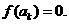 。
。
13.【答案】14
【解析】函數 在
在 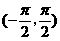 是增函數,顯然又為奇函數,函數圖象關于原點對稱,因為
是增函數,顯然又為奇函數,函數圖象關于原點對稱,因為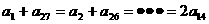 ,
, 
所以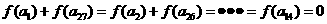 ,所以當
,所以當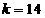 時,
時,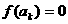 .
.
14.某地街道呈現東——西、南——北向的網絡狀,相鄰街距都為1,兩街道相交的點稱為格點。若以相互垂直的兩條街道為軸建立直角坐標系,現有下述格點(-2,2),(3,1),(3,4),(-2,3),(4,5)為報刊零售店,請確定一個格點 ________為發行站,使5個零售點沿街道發行站之間路程的和最短。
14.【答案】(3,3)
【解析】設發行站的位置為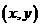 ,零售點到發行站的距離為
,零售點到發行站的距離為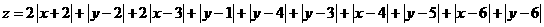 ,這六個點的橫縱坐標的平均值為
,這六個點的橫縱坐標的平均值為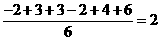 ,
,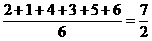 ,記
,記
A(2,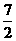 ),畫出圖形可知,發行站的位置應該在點A附近,代入附近的點的坐標進行比較可知,在(3,3)處z取得最小值。
),畫出圖形可知,發行站的位置應該在點A附近,代入附近的點的坐標進行比較可知,在(3,3)處z取得最小值。