22.(3分+5分+8分)如圖,已知曲線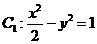 ,曲線
,曲線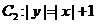 ,P是平面上一點,若存在過點P的直線與
,P是平面上一點,若存在過點P的直線與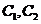 都有公共點,則稱P為“C1—C2型點”.
都有公共點,則稱P為“C1—C2型點”.
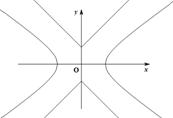
(1)在正確證明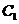 的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
的左焦點是“C1—C2型點”時,要使用一條過該焦點的直線,試寫出一條這樣的直線的方程(不要求驗證);
(2)設直線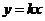 與
與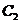 有公共點,求證
有公共點,求證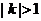 ,進而證明原點不是“C1—C2型點”;
,進而證明原點不是“C1—C2型點”;
(3)求證:圓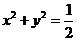 內的點都不是“C1—C2型點”.
內的點都不是“C1—C2型點”.
【解答】:(1)C1的左焦點為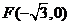 ,過F的直線
,過F的直線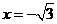 與C1交于
與C1交于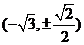 ,與C2交于
,與C2交于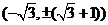 ,故C1的左焦點為“C1-C2型點”,且直線可以為
,故C1的左焦點為“C1-C2型點”,且直線可以為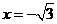 ;
;
(2)直線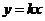 與C2有交點,則
與C2有交點,則
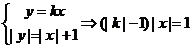 ,若方程組有解,則必須
,若方程組有解,則必須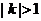 ;
;
直線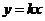 與C2有交點,則
與C2有交點,則
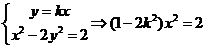 ,若方程組有解,則必須
,若方程組有解,則必須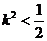
故直線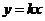 至多與曲線C1和C2中的一條有交點,即原點不是“C1-C2型點”。
至多與曲線C1和C2中的一條有交點,即原點不是“C1-C2型點”。
(3)顯然過圓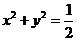 內一點的直線
內一點的直線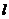 若與曲線C1有交點,則斜率必存在;
若與曲線C1有交點,則斜率必存在;
根據對稱性,不妨設直線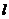 斜率存在且與曲線C2交于點
斜率存在且與曲線C2交于點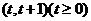 ,則
,則
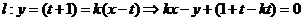
直線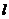 與圓
與圓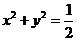 內部有交點,故
內部有交點,故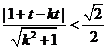
化簡得,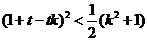 。。。。。。。。。。。。①
。。。。。。。。。。。。①
若直線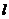 與曲線C1有交點,則
與曲線C1有交點,則
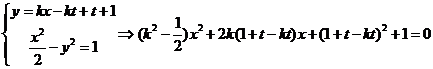
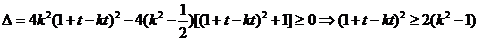
化簡得,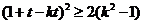 。。。。。②
。。。。。②
由①②得,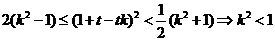
但此時,因為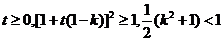 ,即①式不成立;
,即①式不成立;
當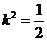 時,①式也不成立
時,①式也不成立
綜上,直線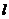 若與圓
若與圓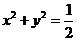 內有交點,則不可能同時與曲線C1和C2有交點,
內有交點,則不可能同時與曲線C1和C2有交點,
即圓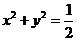 內的點都不是“C1-C2型點” .
內的點都不是“C1-C2型點” .
23.(3 分+6分+9分)給定常數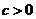 ,定義函數
,定義函數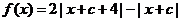 ,數列
,數列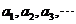 滿足
滿足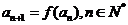 .
.
(1)若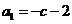 ,求
,求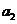 及
及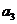 ;(2)求證:對任意
;(2)求證:對任意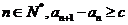 ,;
,;
(3)是否存在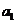 ,使得
,使得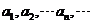 成等差數列?若存在,求出所有這樣的
成等差數列?若存在,求出所有這樣的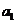 ,若不存在,說明理由.
,若不存在,說明理由.
【解答】:(1)因為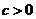 ,
,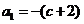 ,故
,故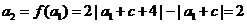 ,
,
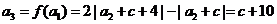
(2)要證明原命題,只需證明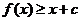 對任意
對任意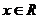 都成立,
都成立,
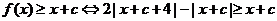
即只需證明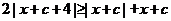
若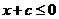 ,顯然有
,顯然有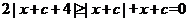 成立;
成立;
若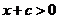 ,則
,則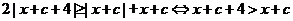 顯然成立
顯然成立
綜上,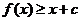 恒成立,即對任意的
恒成立,即對任意的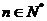 ,
,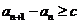
(3)由(2)知,若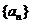 為等差數列,則公差
為等差數列,則公差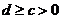 ,故n無限增大時,總有
,故n無限增大時,總有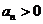
此時,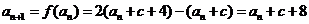
即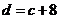
故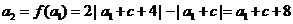 ,
,
即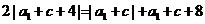 ,
,
當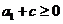 時,等式成立,且
時,等式成立,且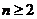 時,
時,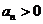 ,此時
,此時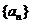 為等差數列,滿足題意;
為等差數列,滿足題意;
若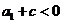 ,則
,則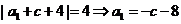 ,
,
此時,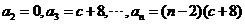 也滿足題意;
也滿足題意;
綜上,滿足題意的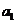 的取值范圍是
的取值范圍是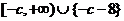 .
.











