一.填空題
1.計算: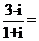 (
(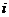 為虛數單位).
為虛數單位).
【答案】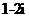
【解析】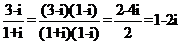 .
.
【點評】本題著重考查復數的除法運算,首先,將分子、分母同乘以分母的共軛復數,將分母實數化即可.
2.若集合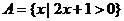 ,
,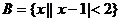 ,則
,則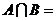 .
.
【答案】 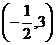
【解析】根據集合A 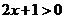 ,解得
,解得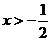 ,由
,由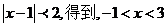 ,所以
,所以
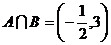 .
.
【點評】本題考查集合的概念和性質的運用,同時考查了一元一次不等式和絕對值不等式的解法.解決此類問題,首先分清集合的元素的構成,然后,借助于數軸或韋恩圖解決.
3.函數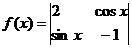 的值域是 .
的值域是 .
【答案】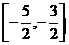
【解析】根據題目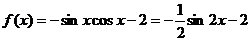 ,因為
,因為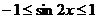 ,所以
,所以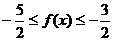 .
.
【點評】本題主要考查行列式的基本運算、三角函數的范圍、二倍角公式,屬于容易題,難度較小.考綱中明確要求掌握二階行列式的運算性質.
4.若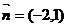 是直線
是直線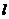 的一個法向量,則
的一個法向量,則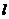 的傾斜角的大小為 (結果用反三角函數值表示).
的傾斜角的大小為 (結果用反三角函數值表示).
【答案】
【解析】設直線的傾斜角為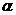 ,則
,則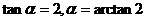 .
.
【點評】本題主要考查直線的方向向量、直線的傾斜角與斜率的關系、反三角函數的表示.直線的傾斜角的取值情況一定要注意,屬于低檔題,難度較小.
5.在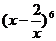 的二項展開式中,常數項等于 .
的二項展開式中,常數項等于 .
【答案】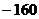
【解析】根據所給二項式的構成,構成的常數項只有一項,就是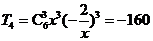 .
.
【點評】本題主要考查二項式定理.對于二項式的展開式要清楚,特別注意常數項的構成.屬于中檔題.
6.有一列正方體,棱長組成以1為首項、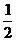 為公比的等比數列,體積分別記為
為公比的等比數列,體積分別記為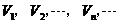 ,則
,則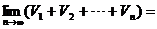 .
.
【答案】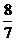
【解析】由正方體的棱長組成以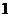 為首項,
為首項,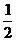 為公比的等比數列,可知它們的體積則組成了一個以1為首項,
為公比的等比數列,可知它們的體積則組成了一個以1為首項,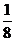 為公比的等比數列,因此,
為公比的等比數列,因此,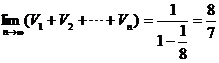 .
.
【點評】本題主要考查無窮遞縮等比數列的極限、等比數列的通項公式、等比數列的定義.考查知識較綜合.
7.已知函數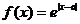 (
(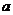 為常數).若
為常數).若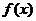 在區間
在區間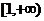 上是增函數,則
上是增函數,則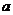 的取值范圍是 .
的取值范圍是 .
【答案】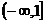
【解析】根據函數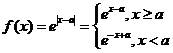 看出當
看出當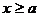 時函數增函數,而已知函數
時函數增函數,而已知函數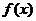 在區間
在區間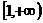 上為增函數,所以
上為增函數,所以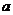 的取值范圍為:
的取值范圍為: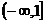 .
.
【點評】本題主要考查指數函數單調性,復合函數的單調性的判斷,分類討論在求解數學問題中的運用.本題容易產生增根,要注意取舍,切勿隨意處理,導致不必要的錯誤.本題屬于中低檔題目,難度適中.
8.若一個圓錐的側面展開圖是面積為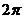 的半圓面,則該圓錐的體積為 .
的半圓面,則該圓錐的體積為 .
【答案】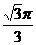
【解析】根據該圓錐的底面圓的半徑為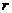 ,母線長為
,母線長為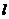 ,根據條件得到
,根據條件得到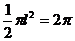 ,解得母線長
,解得母線長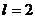 ,
,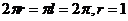 所以該圓錐的體積為:
所以該圓錐的體積為: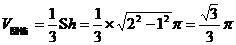 .
.
【點評】本題主要考查空間幾何體的體積公式和側面展開圖.審清題意,所求的為體積,不是其他的量,分清圖形在展開前后的變化;其次,對空間幾何體的體積公式要記準記牢,屬于中低檔題.
9.已知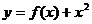 是奇函數,且
是奇函數,且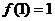 ,若
,若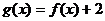 ,則
,則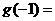 .
.
【答案】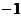
【解析】因為函數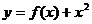 為奇函數,所以
為奇函數,所以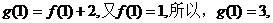
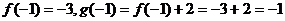 .
.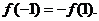
【點評】本題主要考查函數的奇偶性.在運用此性質解題時要注意:函數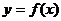 為奇函數,所以有
為奇函數,所以有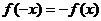 這個條件的運用,平時要加強這方面的訓練,本題屬于中檔題,難度適中.
這個條件的運用,平時要加強這方面的訓練,本題屬于中檔題,難度適中.
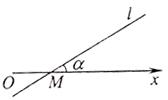
10.如圖,在極坐標系中,過點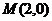 的直線
的直線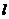 與極軸的夾角
與極軸的夾角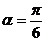 ,若將
,若將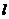 的極坐標方程寫成
的極坐標方程寫成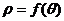 的形式,則
的形式,則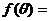 .
.
【答案】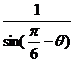
【解析】根據該直線過點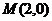 ,可以直接寫出代數形式的方程為:
,可以直接寫出代數形式的方程為: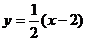 ,將此化成極坐標系下的參數方程即可 ,化簡得
,將此化成極坐標系下的參數方程即可 ,化簡得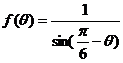 .
.
【點評】本題主要考查極坐標系,本部分為選學內容,幾乎年年都有所涉及,題目類型以小題為主,復習時,注意掌握基本規律和基礎知識即可.對于不常見的曲線的參數方程不作要求.本題屬于中檔題,難度適中.
11.三位同學參加跳高、跳遠、鉛球項目的比賽,若每人都選擇其中兩個項目,則有且僅有兩人選擇的項目完全相同的概率是 (結果用最簡分數表示).
【答案】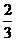
【解析】一共有27種取法,其中有且只有兩個人選擇相同的項目的取法共有18種,所以根據古典概型得到此種情況下的概率為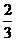 .
.
【點評】本題主要考查排列組合概率問題、古典概型.要分清基本事件數和基本事件總數.本題屬于中檔題.
12.在平行四邊形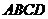 中,
中,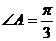 ,邊
,邊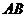 、
、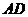 的長分別為2、1,若
的長分別為2、1,若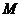 、
、 分別是邊
分別是邊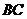 、
、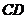 上的點,且滿足
上的點,且滿足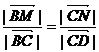 ,則
,則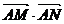 的取值范圍是 .
的取值范圍是 .
【答案】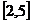
【解析】以向量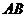 所在直線為
所在直線為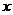 軸,以向量
軸,以向量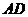 所在直線為
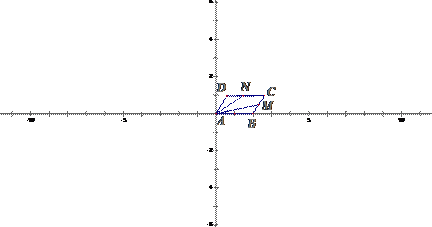
所在直線為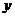 軸建立平面直角坐標系,如圖所示,因為
軸建立平面直角坐標系,如圖所示,因為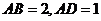 ,所以
,所以 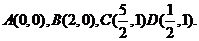 設
設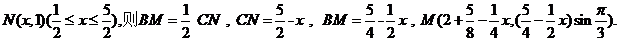 根據題意,有
根據題意,有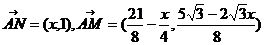 .
.
所以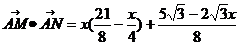
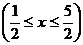 ,所以
,所以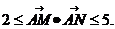
【點評】本題主要考查平面向量的基本運算、概念、平面向量的數量積的運算律.做題時,要切實注意條件的運用.本題屬于中檔題,難度適中.
13.已知函數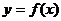 的圖象是折線段
的圖象是折線段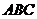 ,其中
,其中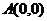 、
、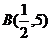 、
、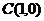 ,
,
函數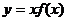 (
(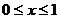 )的圖象與
)的圖象與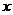 軸圍成的圖形的面積為 .
軸圍成的圖形的面積為 .
【答案】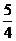
【解析】根據題意得到,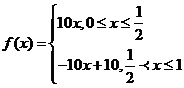 從而得到
從而得到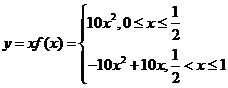 所以圍成的面積為
所以圍成的面積為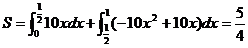 ,所以圍成的圖形的面積為
,所以圍成的圖形的面積為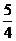 .
.
【點評】本題主要考查函數的圖象與性質,函數的解析式的求解方法、定積分在求解平面圖形中的運用.突出體現數形結合思想,本題綜合性較強,需要較強的分析問題和解決問題的能力,在以后的練習中加強這方面的訓練,本題屬于中高檔試題,難度較大.
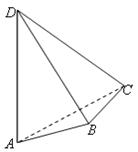
14.如圖,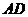 與
與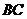 是四面體
是四面體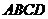 中互相垂直的棱,
中互相垂直的棱,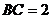 ,若
,若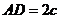 ,且
,且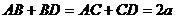 ,其中
,其中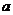 、
、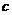 為常數,則四面體
為常數,則四面體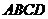 的體積的最大值是 .
的體積的最大值是 .
【答案】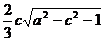
【解析】據題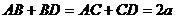 ,也就是說,線段
,也就是說,線段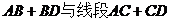 的長度是定值,因為棱
的長度是定值,因為棱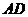 與棱
與棱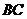 互相垂直,當
互相垂直,當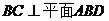 時,此時有最大值,此時最大值為:
時,此時有最大值,此時最大值為: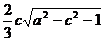 .
.
【點評】本題主要考查空間四面體的體積公式、空間中點線面的關系.本題主要考慮根據已知條件構造體積表達式,這是解決問題的關鍵,本題綜合性強,運算量較大.屬于中高檔試題.











