一、填空題(56分)
1、函數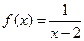 的反函數為
的反函數為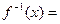 。
。
2、若全集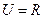 ,集合
,集合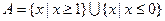 ,則
,則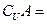 。
。
3、設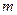 為常數,若點
為常數,若點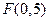 是雙曲線
是雙曲線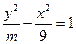 的一個焦點,則
的一個焦點,則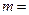 。
。
4、不等式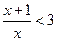 的解為 。
的解為 。
5、在極坐標系中,直線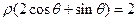 與直線
與直線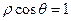 的夾角大小為 。
的夾角大小為 。
6、在相距2千米的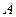 、
、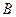 兩點處測量目標
兩點處測量目標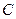 ,若
,若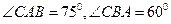 ,則
,則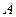 、
、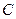 兩點之間的距離是 千米。
兩點之間的距離是 千米。
7、若圓錐的側面積為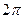 ,底面積為
,底面積為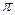 ,則該圓錐的體積為 。
,則該圓錐的體積為 。
8、函數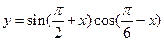 的最大值為 。
的最大值為 。
9、馬老師從課本上抄錄一個隨機變量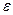 的概率分布律如下表
的概率分布律如下表
請小牛同學計算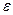 的數學期望,盡管“!”處無法完全看清,且兩個“?”處字跡模糊,但能肯定這兩個“?”處的數值相同。據此,小牛給出了正確答案
的數學期望,盡管“!”處無法完全看清,且兩個“?”處字跡模糊,但能肯定這兩個“?”處的數值相同。據此,小牛給出了正確答案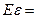 。
。

10、行列式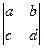 (
(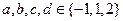 )的所有可能值中,最大的是 。
)的所有可能值中,最大的是 。
11、在正三角形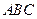 中,
中,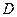 是
是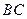 上的點,
上的點,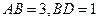 ,則
,則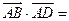 。
。
12、隨機抽取9個同學中,至少有2個同學在同一月出生的概率是 (默認每月天數相同,結果精確到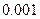 )。
)。
13、設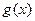 是定義在
是定義在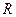 上、以1為周期的函數,若
上、以1為周期的函數,若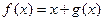 在
在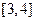 上的值域為
上的值域為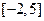 ,則
,則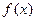 在區間
在區間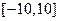 上的值域為 。
上的值域為 。
14、已知點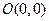 、
、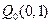 和
和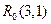 ,記
,記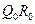 的中點為
的中點為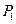 ,取
,取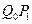 和
和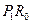 中的一條,記其端點為
中的一條,記其端點為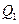 、
、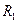 ,使之滿足
,使之滿足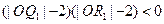 ;記
;記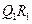 的中點為
的中點為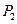 ,取
,取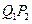 和
和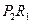 中的一條,記其端點為
中的一條,記其端點為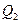 、
、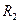 ,使之滿足
,使之滿足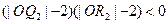 ;依次下去,得到點
;依次下去,得到點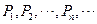 ,則
,則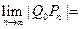 。
。
二、選擇題(20分)
15、若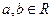 ,且
,且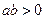 ,則下列不等式中,恒成立的是〖答〗( )
,則下列不等式中,恒成立的是〖答〗( )
A 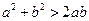 B
B 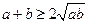 C
C 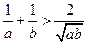 D
D 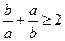
16、下列函數中,既是偶函數,又是在區間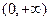 上單調遞減的函數為〖答〗( )
上單調遞減的函數為〖答〗( )
A 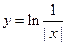 B
B 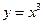 C
C 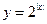 D
D 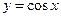
17、設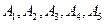 是空間中給定的5個不同的點,則使
是空間中給定的5個不同的點,則使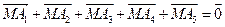 成立的點
成立的點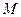 的個數為〖答〗( )
的個數為〖答〗( )
A 0 B 1 C 5 D 10
18、設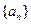 是各項為正數的無窮數列,
是各項為正數的無窮數列,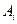 是邊長為
是邊長為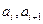 的矩形面積(
的矩形面積(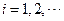 ),則
),則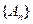 為等比數列的充要條件為〖答〗( )
為等比數列的充要條件為〖答〗( )
A 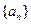 是等比數列。
是等比數列。
B 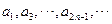 或
或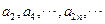 是等比數列。
是等比數列。
C 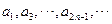 和
和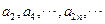 均是等比數列。
均是等比數列。
D 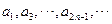 和
和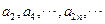 均是等比數列,且公比相同。
均是等比數列,且公比相同。
三、解答題(74分)
19、(12分)已知復數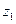 滿足
滿足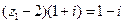 (
(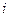 為虛數單位),復數
為虛數單位),復數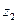 的虛部為
的虛部為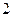 ,
,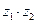 是實數,求
是實數,求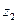 。
。
20、(12分)已知函數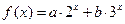 ,其中常數
,其中常數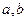 滿足
滿足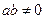 。
。
⑴ 若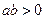 ,判斷函數
,判斷函數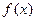 的單調性;
的單調性;
⑵ 若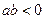 ,求
,求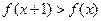 時
時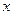 的取值范圍。
的取值范圍。
21、(14分)已知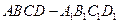 是底面邊長為1的正四棱柱,
是底面邊長為1的正四棱柱,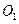 是
是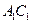 和
和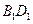 的交點。
的交點。

⑴ 設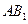 與底面
與底面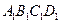 所成的角的大小為
所成的角的大小為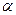 ,二面角
,二面角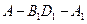 的大小為
的大小為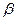 。
。
求證: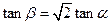 ;
;
⑵ 若點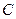 到平面
到平面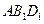 的距離為
的距離為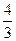 ,求正四棱柱
,求正四棱柱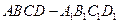 的高。
的高。
22、(18分)已知數列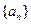 和
和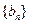 的通項公式分別為
的通項公式分別為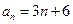 ,
,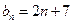 (
(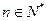 ),將集合
),將集合
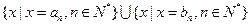 中的元素從小到大依次排列,構成數列
中的元素從小到大依次排列,構成數列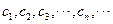 。
。
⑴ 求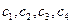 ;
;
⑵ 求證:在數列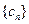 中、但不在數列
中、但不在數列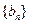 中的項恰為
中的項恰為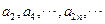 ;
;
⑶ 求數列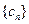 的通項公式。
的通項公式。
23、(18分)已知平面上的線段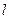 及點
及點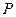 ,在
,在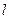 上任取一點
上任取一點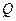 ,線段
,線段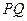 長度的最小值稱為點
長度的最小值稱為點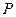 到線段
到線段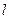 的距離,記作
的距離,記作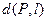 。
。
⑴ 求點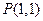 到線段
到線段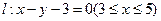 的距離
的距離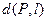 ;
;
⑵ 設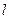 是長為2的線段,求點集
是長為2的線段,求點集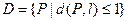 所表示圖形的面積;
所表示圖形的面積;
⑶ 寫出到兩條線段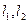 距離相等的點的集合
距離相等的點的集合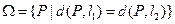 ,其中
,其中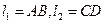 ,
,
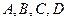 是下列三組點中的一組。對于下列三組點只需選做一種,滿分分別是①2分,②6分,③8分;若選擇了多于一種的情形,則按照序號較小的解答計分。
是下列三組點中的一組。對于下列三組點只需選做一種,滿分分別是①2分,②6分,③8分;若選擇了多于一種的情形,則按照序號較小的解答計分。
① 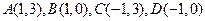 。
。
② 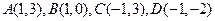 。
。
③ 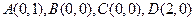 。
。











