22.(4+6+6=16分)在平面直角坐標系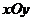 中,已知雙曲線
中,已知雙曲線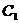 :
: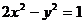 .
.
(1)過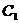 的左頂點引
的左頂點引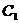 的一條漸進線的平行線,求該直線與另一條漸進線及
的一條漸進線的平行線,求該直線與另一條漸進線及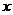 軸圍成的三角形的面積;
軸圍成的三角形的面積;
(2)設(shè)斜率為1的直線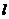 交
交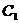 于
于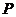 、
、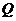 兩點,若
兩點,若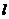 與圓
與圓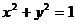 相切,求證:
相切,求證: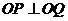 ;
;
(3)設(shè)橢圓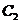 :
: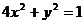 ,若
,若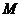 、
、 分別是
分別是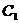 、
、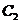 上的動點,且
上的動點,且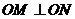 ,求證:
,求證: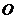 到直線
到直線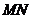 的距離是定值.
的距離是定值.
【答案及解析】
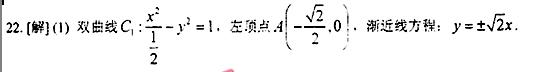
過點A與漸近線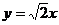 平行的直線方程為
平行的直線方程為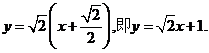
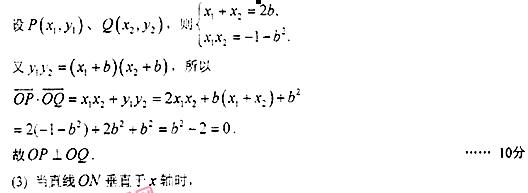
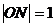 ,
,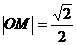 ,則
,則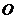 到直線
到直線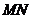 的距離為
的距離為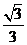 .
.
設(shè)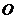 到直線
到直線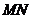 的距離為
的距離為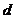 .
.
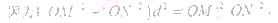

【點評】本題主要考查雙曲線的概念、標準方程、幾何性質(zhì)及其直線與雙曲線的關(guān)系、橢圓的標準方程和圓的有關(guān)性質(zhì).特別要注意直線與雙曲線的關(guān)系問題,在雙曲線當(dāng)中,最特殊的為等軸雙曲線,它的離心率為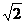 ,它的漸近線為
,它的漸近線為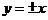 ,并且相互垂直,這些性質(zhì)的運用可以大大節(jié)省解題時間,本題屬于中檔題 .
,并且相互垂直,這些性質(zhì)的運用可以大大節(jié)省解題時間,本題屬于中檔題 .
23.(4+6+8=18分)對于數(shù)集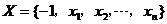 ,其中
,其中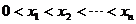 ,
,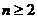 ,定義向量集
,定義向量集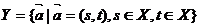 ,若對任意
,若對任意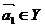 ,存在
,存在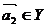 ,使得
,使得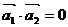 ,則稱
,則稱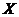 具有性質(zhì)
具有性質(zhì)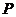 .例如
.例如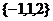 具有性質(zhì)
具有性質(zhì)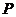 .
.
(1)若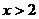 ,且
,且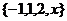 具有性質(zhì)
具有性質(zhì)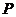 ,求
,求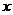 的值;
的值;
(2)若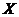 具有性質(zhì)
具有性質(zhì)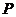 ,求證:
,求證: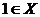 ,且當(dāng)
,且當(dāng)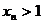 時,
時,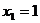 ;
;
(3)若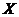 具有性質(zhì)
具有性質(zhì)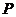 ,且
,且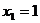 、
、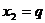 (
(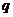 為常數(shù)),求有窮數(shù)列
為常數(shù)),求有窮數(shù)列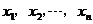 的通項公式.
的通項公式.
【答案及解析】
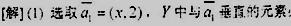 必有形式
必有形式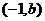



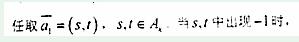 顯然有
顯然有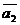 滿足
滿足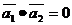
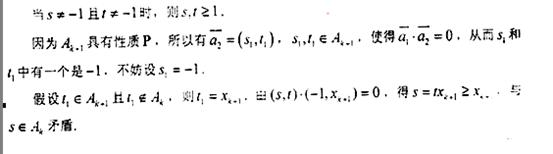



【點評】本題主要考查數(shù)集、集合的基本性質(zhì)、元素與集合的關(guān)系等基礎(chǔ)知識,本題屬于信息給予題,通過定義“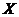 具有性質(zhì)
具有性質(zhì)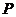 ”這一概念,考查考生分析探究及推理論證的能力.綜合考查集合的基本運算,集合問題一直是近幾年的命題重點內(nèi)容,應(yīng)引起足夠的重視.
”這一概念,考查考生分析探究及推理論證的能力.綜合考查集合的基本運算,集合問題一直是近幾年的命題重點內(nèi)容,應(yīng)引起足夠的重視.











