二、選擇題(20分)
15.若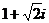 是關于
是關于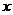 的實系數方程
的實系數方程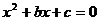 的一個復數根,則( )
的一個復數根,則( )
A.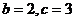 B.
B.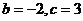 C.
C.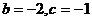 D.
D.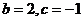
【答案】 B
【解析】根據實系數方程的根的特點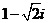 也是該方程的另一個根,所以
也是該方程的另一個根,所以
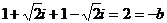 ,即
,即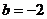 ,
,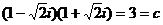 ,故答案選擇B.
,故答案選擇B.
【點評】本題主要考查實系數方程的根的問題及其性質、復數的代數形式的四則運算,屬于中檔題,注重對基本知識和基本技巧的考查,復習時要特別注意.
16.在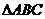 中,若
中,若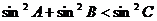 ,則
,則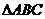 的形狀是( )
的形狀是( )
A.銳角三角形 B.直角三角形 C.鈍角三角形 D.不能確定
【答案】C
【解析】由正弦定理,得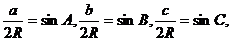
 代入得到
代入得到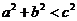 ,
,
由余弦定理的推理得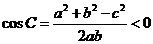 ,所以C為鈍角,所以該三角形為鈍角三角形.故選擇A.
,所以C為鈍角,所以該三角形為鈍角三角形.故選擇A.
【點評】本題主要考查正弦定理及其推理、余弦定理的運用.主要抓住所給式子的結構來選擇定理,如果出現了角度的正弦值就選擇正弦定理,如果出現角度的余弦值就選擇余弦定理.本題屬于中檔題.
17.設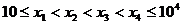 ,
,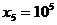 ,隨機變量
,隨機變量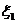 取值
取值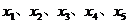 的概率均為
的概率均為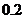 ,隨機變量
,隨機變量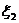 取值
取值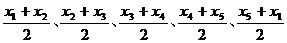 的概率也均為
的概率也均為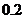 ,若記
,若記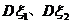 分別為
分別為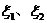 的方差,則( )
的方差,則( )
A.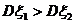 B.
B.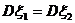
C.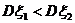 D.
D.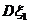 與
與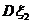 的大小關系與
的大小關系與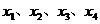 的取值有關
的取值有關
【答案】 A
【解析】 由隨機變量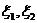 的取值情況,它們的平均數分別為:
的取值情況,它們的平均數分別為: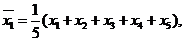 ,
,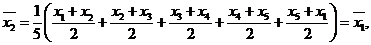
且隨機變量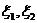 的概率都為
的概率都為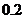 ,所以有
,所以有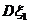 >
>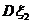 . 故選擇A.
. 故選擇A.
【點評】本題主要考查離散型隨機變量的期望和方差公式.記牢公式是解決此類問題的前提和基礎,本題屬于中檔題.
18.設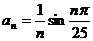 ,
,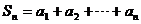 ,在
,在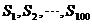 中,正數的個數是( )
中,正數的個數是( )
A.25 B.50 C.75 D.100
【答案】C
【解析】依據正弦函數的周期性,可以找其中等于零或者小于零的項.
【點評】本題主要考查正弦函數的圖象和性質和間接法解題.解決此類問題主要找到規律,從題目出發可以看出來相鄰的14項的和為0,這就是規律,考查綜合分析問題和解決問題的能力.
三、解答題(74分):
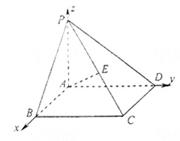
19.(6+6=12分)如圖,在四棱錐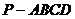 中,底面
中,底面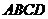 是矩形,
是矩形,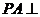 底面
底面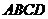 ,
,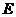 是
是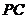 的中點,已知
的中點,已知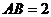 ,
,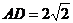 ,
,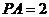 ,求:
,求:
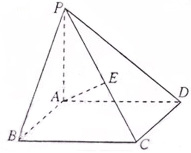
(1)三角形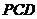 的面積;
的面積;
(2)異面直線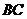 與
與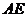 所成的角的大小.
所成的角的大小.
【答案及解析】

所以三角形PCD的面積為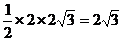 ................6分
................6分

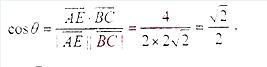
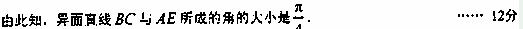
【點評】本題主要考查直線與直線、直線與平面的位置關系,考查空間想象能力和推理論證能力.綜合考查空間中兩條異面直線所成的角的求解,同時考查空間幾何體的體積公式的運用.本題源于《必修2》立體幾何章節復習題,復習時應注重課本,容易出現找錯角的情況,要考慮全面,考查空間想象能力,屬于中檔題.
20.(6+8=14分)已知函數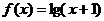 .
.
(1)若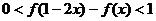 ,求
,求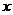 的取值范圍;
的取值范圍;
(2)若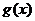 是以2為周期的偶函數,且當
是以2為周期的偶函數,且當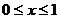 時,有
時,有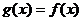 ,求函數
,求函數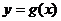 (
(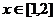 )的反函數.
)的反函數.
【答案及解析】
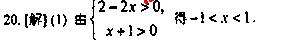
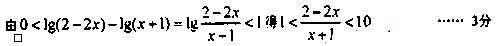
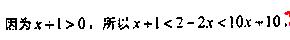 ,
,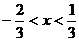
【點評】本題主要考查函數的概念、性質、分段函數等基礎知識.考查數形結合思想,熟練掌握指數函數、對數函數、冪函數的圖象與性質,屬于中檔題.
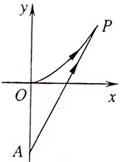 21.(6+8=14分)海事救援船對一艘失事船進行定位:以失事船的當前位置為原點,以正北方向為
21.(6+8=14分)海事救援船對一艘失事船進行定位:以失事船的當前位置為原點,以正北方向為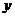 軸正方向建立平面直角坐標系(以1海里為單位長度),則救援船恰好在失事船正南方向12海里
軸正方向建立平面直角坐標系(以1海里為單位長度),則救援船恰好在失事船正南方向12海里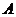 處,如圖.現假設:①失事船的移動路徑可視為拋物線
處,如圖.現假設:①失事船的移動路徑可視為拋物線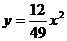 ;②定位后救援船即刻沿直線勻速前往救援;③救援船出發
;②定位后救援船即刻沿直線勻速前往救援;③救援船出發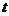 小時后,失事船所在位置的橫坐標為
小時后,失事船所在位置的橫坐標為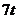 .
.
(1)當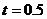 時,寫出失事船所在位置
時,寫出失事船所在位置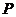 的縱坐標.若此時兩船恰好會合,求
的縱坐標.若此時兩船恰好會合,求
救援船速度的大小和方向;
(2)問救援船的時速至少是多少海里才能追上失事船?











