三.解答題(本大題滿分78分)本大題共5題,解答下列各題必須在答題紙相應的編號規定區域內寫出必要的步驟
19(本題滿分14分)
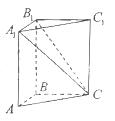
如圖,在直三棱柱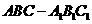 中,
中,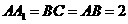 ,
,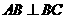 ,求二面角
,求二面角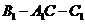 的大小。
的大小。

20(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2小題滿分8分。有時可用函數
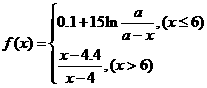 描述學習某學科知識的掌握程度,其中x表示某學科知識的學習次數(
描述學習某學科知識的掌握程度,其中x表示某學科知識的學習次數(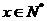 ),
),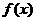 表示對該學科知識的掌握程度,正實數a與學科知識有關。
表示對該學科知識的掌握程度,正實數a與學科知識有關。
(1)證明:當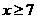 時,掌握程度的增加量
時,掌握程度的增加量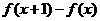 總是下降;
總是下降;
(2)根據經驗,學科甲、乙、丙對應的a的取值區間分別為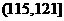 ,
,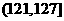 ,
,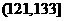 。當學習某學科知識6次時,掌握程度是85%,請確定相應的學科。
。當學習某學科知識6次時,掌握程度是85%,請確定相應的學科。
21.(本題滿分16分)本題共有2個小題,第1小題滿分8分,第2小題滿分8分。
已知雙曲線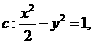 設過點
設過點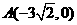 的直線l的方向向量
的直線l的方向向量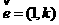
(1)當直線l與雙曲線C的一條漸近線m平行時,求直線l的方程及l與m的距離;
(2)證明:當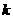 >
>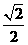 時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為
時,在雙曲線C的右支上不存在點Q,使之到直線l的距離為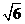 。
。
22.(本題滿分16分)本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分6分。
已知函數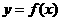 的反函數。定義:若對給定的實數
的反函數。定義:若對給定的實數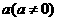 ,函數
,函數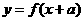 與
與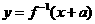 互為反函數,則稱
互為反函數,則稱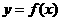 滿足“
滿足“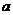 和性質”;若函數
和性質”;若函數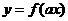 與
與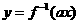 互為反函數,則稱
互為反函數,則稱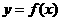 滿足“
滿足“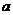 積性質”。
積性質”。
(1)判斷函數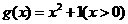 是否滿足“1和性質”,并說明理由;
是否滿足“1和性質”,并說明理由;
(2)求所有滿足“2和性質”的一次函數;
(3)設函數 對任何
對任何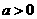 ,滿足“
,滿足“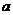 積性質”。求
積性質”。求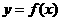 的表達式。
的表達式。
23.(本題滿分18分)本題共有3個小題,第1小題滿分5分,第2小題滿分5分,第3小題滿分8分。
已知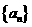 是公差為
是公差為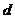 的等差數列,
的等差數列,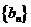 是公比為
是公比為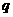 的等比數列。
的等比數列。
(1)若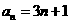 ,是否存在
,是否存在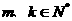 ,有
,有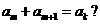 說明理由;
說明理由;
(2)找出所有數列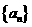 和
和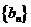 ,使對一切
,使對一切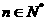 ,
,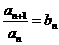 ,并說明理由;
,并說明理由;
(3)若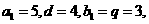 試確定所有的
試確定所有的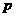 ,使數列
,使數列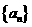 中存在某個連續
中存在某個連續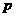 項的和是數列
項的和是數列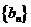 中的一項,請證明。
中的一項,請證明。