三、解答題:本大題共6小題,共75分,解答應寫出文字說明、說明過程或演算步 驟.
驟.
16. (本小題滿分12分)
已知函數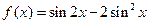
(I)求函數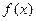 的最小正周期;
的最小正周期;
(Ⅱ) 求函數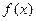 的最大值及
的最大值及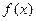 取最大值時
取最大值時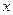 的集合.
的集合.
16.【命題意圖】本題考查了三角函數的恒等變換公式、三角函數 的圖象與性質等,關鍵是運算能力的考查及其應用。對于(1)中,先對三角函數進行恒等變換,利用變換后的三角函數的性質確定最小正周期;對于(2)
的圖象與性質等,關鍵是運算能力的考查及其應用。對于(1)中,先對三角函數進行恒等變換,利用變換后的三角函數的性質確定最小正周期;對于(2) 中,直接利用(1)的變換式,求解函數的最大值及最大值時x的集合。
中,直接利用(1)的變換式,求解函數的最大值及最大值時x的集合。
【參考答案】
解:(Ⅰ)因為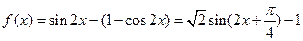 .
.
所以函數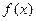 的最小正周期為
的最小正周期為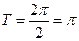 .
.
(Ⅱ)由(Ⅰ)知,當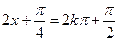 ,即
,即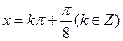 時,
時,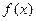 取最大值
取最大值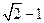 .因此函數
.因此函數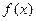 取最大值時
取最大值時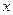 的集合為
的集合為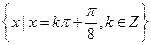 .
.
【點評】求解三角函數值問題,往往通過同角三角函數基本關系式、三角函數的恒等變換、解析式的化簡與變形、相應的函數圖象及其對應的性質的綜合分析與考查,往往是高考中的常見問題之一,也是考查面變換比較多的題型之一.關鍵是正確掌握與應用相應的三角函數公式。
17. (本小題滿分12分)
為了對某課題進行研究,用 分層抽樣方法從三所高校A,B,C的相關人員中,抽取若干人組成研究小組,有關數據見下表(單位:人)
分層抽樣方法從三所高校A,B,C的相關人員中,抽取若干人組成研究小組,有關數據見下表(單位:人)
高校 | 相關人數 | 抽取人數 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(I)求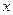 ,
,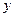 ;
;
(Ⅱ)若從高校B、C抽取的人 中選2人作專題發言,求這2人都
中選2人作專題發言,求這2人都 來自高校C的概率.
來自高校C的概率.
17.【命題意圖】本題考查了分層抽樣的特征與運算,以及古典概型的概率計算問題。關鍵是表格中數據的分析與處理。對于(1),直接利用分層抽樣的特征建立相關的比例式,求解對應的參數值;對于(2),根據(1)計算的抽取人數,寫出相應的基本事件數, 利用古典概型的概率公式求解對應的概率。
利用古典概型的概率公式求解對應的概率。

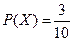 .
.
故選中的2人都來自高校C的概率為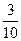 .
.
【點評】通過實際應用問題,主要考查統計及古典概率的求法.解決此類實際應用問題要注意對統計數據的分析和對基本事件分析.關鍵是對統計與古典概率的求法,統計中往往涉及對應的抽樣方法的應用等,它們是一個重點,但通常不難,要認真掌握.
18.(本小題滿分12分)
如圖3所示,在長方體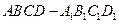 中,AB=AD=1,AA1=2,M是棱CC1的中點.
中,AB=AD=1,AA1=2,M是棱CC1的中點.
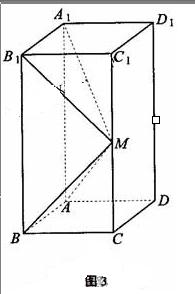
(Ⅰ)求異面直線A1M和C1D1所成的角的正切值;
(Ⅱ)證明:平面ABM⊥平面A1B1M1.
18.【命題意圖】本題考查了立體幾何中點、線、面之間的位置關系的證明問題與夾角的求解問題.對于(1),主要是通過線段的轉化,結合空間圖形的性質,通過三角形來求解對應的異面直線的夾角問題;對于(2),通過空間幾何的分析與判斷,通過線面垂直來判斷面面垂直問題。
【參考答案】
解:(Ⅰ)如圖,因為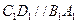 ,所以
,所以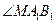 為異面直線
為異面直線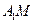 與
與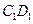 所成的角.
所成的角.
因為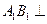 平面
平面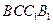 ,所以
,所以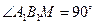 .
.
而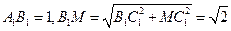 ,故
,故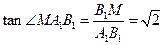 .
.
即異面直線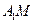 和
和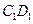 所成的角的正切值為
所成的角的正切值為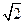 .
.
(Ⅱ)由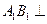 平面
平面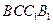 ,
,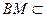 平面
平面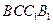 ,得
,得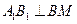 .①
.①
由(Ⅰ)知,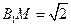 ,又
,又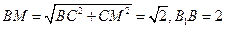 ,所以
,所以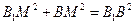 ,從而
,從而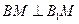 .②
.②
又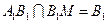 ,再由①,②得
,再由①,②得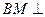 平面
平面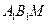 .而
.而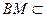 平面
平面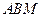 ,因此平面
,因此平面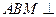 平面
平面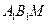 .
.
【點評】空間幾何問題,通常與點、線、面的位置關系的判斷與證明,以及點、線、面之間的角度或長度關系的求解相結合.一般可以通過輔助線的構造結合點、線、面的相應概念、性質、定理判斷與求解相關的問題,也可以通過空間向量知識來達到目的.特別對于圖形的翻折與變換,要加以分析變換前后相應元素之間的關系.
19.(本小題滿分13分)
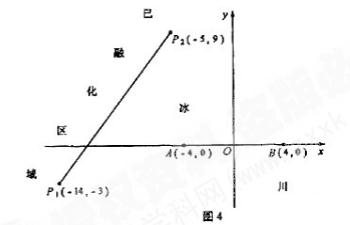
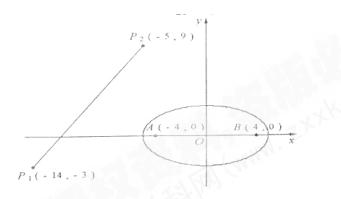
為了考察冰川的融化狀況,一支科考隊在某冰川山上相距8km的A、B兩點各建一個考察基地.視冰川面為平面形,以過A、B兩點的直線為x軸 ,線段AB的垂直平分線為y軸建立平面直角坐標系(圖4).考察范圍為到A、B兩點的距離之和不超過10km的區域.
,線段AB的垂直平分線為y軸建立平面直角坐標系(圖4).考察范圍為到A、B兩點的距離之和不超過10km的區域.
(Ⅰ)求考察區域邊界曲線的方程;
(Ⅱ)如圖4所示,設線段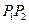 是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍.問:經過多長時間,點A恰好在冰川邊界線上?
是冰川的部分邊界線(不考慮其他邊界),當冰川融化時,邊界線沿與其垂直的方向朝考察區域平行移動,第一年移動0.2km,以后每年移動的距離為前一年的2倍.問:經過多長時間,點A恰好在冰川邊界線上?
19.【命題意圖】本題考查了實際應用問題,橢圓的標準方程與幾何性質,直線與圓錐曲線的位置關系,直線方程,點到直線的距離公式,以及等差數列的相關問題等。對于(1),直接結合題目的敘述情況,利用橢圓的定義,求解相應的橢圓的標準方程;對于(2),先求相應的直線方程,利用點到直線的距離公式,以及等差數列的求和來確定相關的參數值。
【參考答案】
解:(Ⅰ)設邊界曲線上點P的坐標為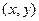 ,則由
,則由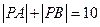 知,點P在以A,B為焦點,長軸長為
知,點P在以A,B為焦點,長軸長為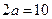 的橢圓上.此時短半軸長
的橢圓上.此時短半軸長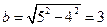 .
.
所以考察區域邊界曲線(如圖)的方程為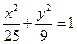 .
.
(Ⅱ)易知過點 的直線方程為
的直線方程為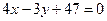 .因此點A到直線
.因此點A到直線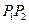 的距離為
的距離為
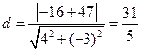 .
.
設經過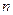 年,點A恰好在冰川邊界線上,則利用等比數列求和公式可得
年,點A恰好在冰川邊界線上,則利用等比數列求和公式可得
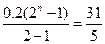 .
.
解得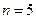 ,即經過5年,點A恰好在冰川邊界線上.
,即經過5年,點A恰好在冰川邊界線上.
【點評】圓錐曲線是歷年高考中比較常見的壓軸題之一,近年高考中其解答難度有逐漸變低的趨勢 .通過解析幾何自身的特點,結合相應的數學知識,比如不等式、數列、函數、向量、導數等相應知識加以綜合,綜合考查各知識點之間的綜合應用,也是考查學生綜合能力的一大考點.這里通過實際問題交匯,綜合相關的知識,難度變小,但考查的知識點變多.
.通過解析幾何自身的特點,結合相應的數學知識,比如不等式、數列、函數、向量、導數等相應知識加以綜合,綜合考查各知識點之間的綜合應用,也是考查學生綜合能力的一大考點.這里通過實際問題交匯,綜合相關的知識,難度變小,但考查的知識點變多.
20.(本小題滿分13分)
給出下面的數表序列:

其中表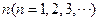 有
有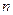 行,第1行的
行,第1行的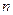 個數是1,3,5,
個數是1,3,5,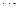 ,2n-1,從第2行起,每行中的每個數都等于它肩上的兩數之和.
,2n-1,從第2行起,每行中的每個數都等于它肩上的兩數之和.
(Ⅰ)寫出表4,驗證表4各行中數的平均數按從上到下的順序構成等比數列,并將結論推廣到表n(n≥3)(不要求證明);
(Ⅱ)每個數表中最后一行都只有一個數,它們構成數列1,4,12, ,記此數列為
,記此數列為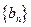 .
.
求和: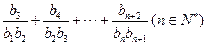 .
.
20.【命題意圖】本題考查了數表 的識別與歸納推理,等比數列的概念與性質,數列求和等,關鍵是閱讀能力、歸納推理能力、運算能力、化歸思維等的應用。對于(1),直接根據數表的規律寫出,再通過求平均數確定其數列的特征,并加以類比推廣;對于(2),得先根據(1)中規律確定bn的通項,再利用相應的公式進行變形,利用裂項法來求解對應的數列求和問題。
的識別與歸納推理,等比數列的概念與性質,數列求和等,關鍵是閱讀能力、歸納推理能力、運算能力、化歸思維等的應用。對于(1),直接根據數表的規律寫出,再通過求平均數確定其數列的特征,并加以類比推廣;對于(2),得先根據(1)中規律確定bn的通項,再利用相應的公式進行變形,利用裂項法來求解對應的數列求和問題。
【參考答案】
解:(Ⅰ)表4為
1 3 5 7
4 8 12
12 20
32
它的第1,2,3,4行中的數的平均數分別是4,8,16,32,它們構成首項為4,公比為2的等比數列.
將這一結論推廣到表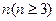 ,即表
,即表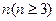 各行中的數的平均數按從上到下的順序構成首項為
各行中的數的平均數按從上到下的順序構成首項為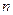 ,公比為2的等比數列.
,公比為2的等比數列.
簡證如下(對考生不作要求)
首先,表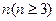 的第1行1,3,5,…,2n-1是等差數列,其平均數為
的第1行1,3,5,…,2n-1是等差數列,其平均數為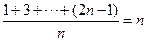 ;
;
其次,若表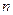 的第
的第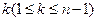 行
行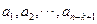 是等差數列,則它的第
是等差數列,則它的第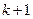 行
行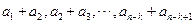 也是等差數列.由等差數列的性質知,表
也是等差數列.由等差數列的性質知,表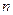 的第
的第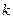 行中的數的平均數與第
行中的數的平均數與第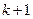 行中的數的平均數分別是
行中的數的平均數分別是
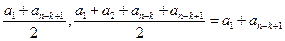 .
.
由此可知,表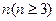 各行中的數都成等差數列,且各行中的數的平均數按從上到下的順序構成首項為
各行中的數都成等差數列,且各行中的數的平均數按從上到下的順序構成首項為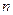 ,公比為2的等比數列.
,公比為2的等比數列.
(Ⅱ)表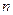 的第1行是1,3,5,…,2n-1,其平均數是
的第1行是1,3,5,…,2n-1,其平均數是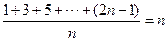 .
.
由(Ⅰ)知,它的各行中的數的平均數按從上到下的順序構成首項為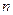 ,公比為2的等比數列(從而它的第
,公比為2的等比數列(從而它的第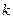 行中的數的
行中的數的 平均數是
平均數是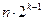 ),于是,表
),于是,表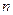 中最后一行的唯一一個數為
中最后一行的唯一一個數為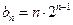 .
.
因此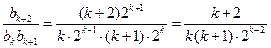
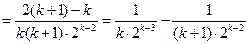 .
.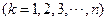
故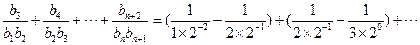
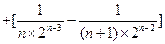
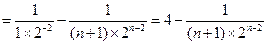
【點評】等差數列與等比數列問題是高考中比較綜合的類型之一,可以與函數、圖象、解析幾何、立體幾何等相關知識加以綜合,關鍵是正確分析對應的項與項之間的關系,加以合理分析,從而正確結合數列的相應公式加以處理與解決相關的數列問題.在這里通過數表形式,結合推理思維,還是要在掌握數列基本知識的基礎上,結合相應的方法(如錯位相減法等),以及與其他知識點的交匯上作文章,要加以重視.
21.(本 小題滿分13分)
小題滿分13分)
已知函數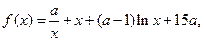 其中
其中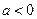 ,且
,且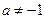 .
.
(Ⅰ)討論函數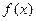 的單調性;
的單調性;
(Ⅱ)設函數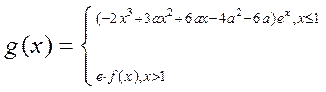 (e是自然對數的底數).是否存在
(e是自然對數的底數).是否存在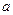 ,使
,使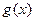 在
在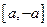 上為減函數?若存在,求
上為減函數?若存在,求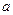 的取值范圍;若不存在
的取值范圍;若不存在 ,請說明理由.
,請說明理由.
21.【命題意圖】本題考查了導數及其應用,考查函數的單調性,分段函數及其性質,存在性問題的探究,通過分類討論等來處理相應的導數問題。對于(1),直接在函數定義域的前提下,加以求導,通過參數的分類討論,確定相應的單調性;對于(2),要結合參數的不同取值,通過分類討論,利用函數的單調性來確定存在性問題。

再設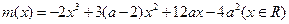 ,則當
,則當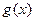 在
在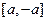 上單調遞減時,
上單調遞減時,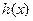 必在
必在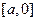 上單調遞減,所以
上單調遞減,所以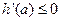 .由于
.由于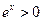 ,因此
,因此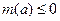 .而
.而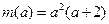 ,所以
,所以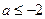 .此時,顯然有
.此時,顯然有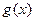 在
在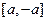 上為減
上為減 函數,當且僅當
函數,當且僅當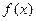 在
在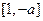 上為減函數,
上為減函數,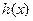 在
在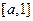 上為減函數,且
上為減函數,且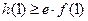 .
.
由(Ⅰ)知,當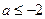 時,
時,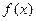 在
在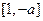 上為減函數.①
上為減函數.①
又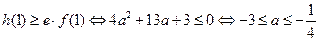 .②
.②
不難知道,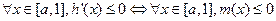 .
.
因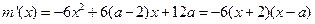 ,令
,令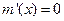 ,則
,則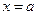 ,或
,或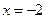 .而
.而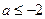 ,于是
,于是
(1) 當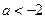 時,若
時,若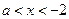 ,則
,則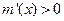 ;若
;若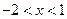 ,則
,則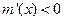 .因而
.因而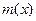 在
在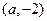 上單調遞增,在
上單調遞增,在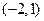 上單調遞減.
上單調遞減.
(2) 當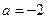 時,
時,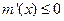 ,
,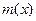 在
在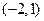 上單調遞減.
上單調遞減.
綜合(1)、(2)知,當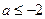 時,
時,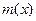 在
在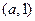 上的最大值為
上的最大值為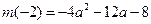 .
.
所以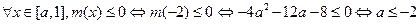 .③
.③
又對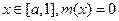 只有當
只有當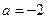 時在
時在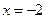 取得,亦即
取得,亦即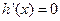 只有當
只有當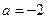 時在
時在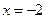 取得.因此,當
取得.因此,當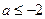 時,
時,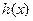 在
在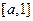 上為減函數.從而由①,②,③知,
上為減函數.從而由①,②,③知,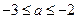 .
.
綜上所述,存在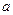 ,使
,使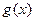 在
在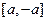 上為減函數,且
上為減函數,且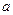 的取值范圍為
的取值范圍為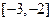 .
.
【點評】利用導 數研究某些函數的單調性與最值,可以解決一些不等式的證明問題,即通過導數作為工具將函數與不等式知識結合起來運用.導數作為一種工具,可以用來處理與函數有關的很多問題,其中證明不等式也是其中具有創新應用的一種,其實質是抓住用導數判斷函數單調性的應用來處理對應函數的單調性問題,從而再轉化為對應的不等式成立問題.
數研究某些函數的單調性與最值,可以解決一些不等式的證明問題,即通過導數作為工具將函數與不等式知識結合起來運用.導數作為一種工具,可以用來處理與函數有關的很多問題,其中證明不等式也是其中具有創新應用的一種,其實質是抓住用導數判斷函數單調性的應用來處理對應函數的單調性問題,從而再轉化為對應的不等式成立問題.











