三.解答題:本大題共6小題,共75分,解答應寫出文字說明、證明過程或演算步驟。
17.(本小題滿分12分)在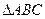 中,角
中,角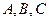 所對的邊分別為
所對的邊分別為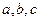 ,且滿足
,且滿足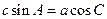 .
.
(I)求角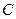 的大小;
的大小;
(II)求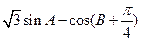 的最大值,并求取得最大值時角
的最大值,并求取得最大值時角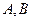 的大小.
的大小.
18. 某商店試銷某種商品20天,獲得如下數據:
日銷售量(件) | 0 | 1 | 2 | 3 |
頻數 | 1 | 5 | 9 | 5 |
試銷結束后(假設該商品的日銷售量的分布規律不變),設某天開始營業時有該商品3件,當天營業結束后檢查存貨,若發現存貨少于2件,則當天進貨補充至3件,否則不進貨,將頻率視為概率。
(Ⅰ)求當天商品不進貨的概率;
(Ⅱ)記X為第二天開始營業時該商品的件數,求X的分布列和數學期望。
19.(本題滿分12分)如圖5,在圓錐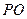 中,已知
中,已知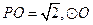 的直徑
的直徑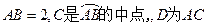 的中點.
的中點.
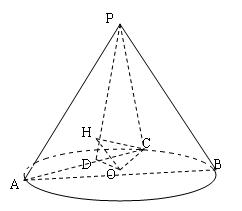
(I)證明: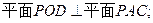
(II)求二面角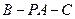 的余弦值.
的余弦值.
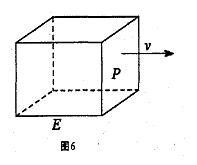
20. 如圖6,長方形物體E在雨中沿面P(面積為S)的垂直方向作勻速移動,速度為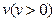 ,雨速沿E移動方向的分速度為
,雨速沿E移動方向的分速度為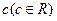 。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與
。E移動時單位時間內的淋雨量包括兩部分:(1)P或P的平行面(只有一個面淋雨)的淋雨量,假設其值與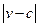 ×S成正比,比例系數為
×S成正比,比例系數為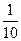 ;(2)其它面的淋雨量之和,其值為
;(2)其它面的淋雨量之和,其值為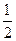 ,記
,記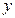 為E移動過程中的總淋雨量,當移動距離d=100,面積S=
為E移動過程中的總淋雨量,當移動距離d=100,面積S=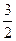 時。
時。
(Ⅰ)寫出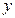 的表達式
的表達式
(Ⅱ)設0<v≤10,0<c≤5,試根據c的不同取值范圍,確定移動速度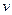 ,使總淋雨量
,使總淋雨量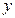 最少。
最少。
解析:(I)由題意知,E移動時單位時間內的淋雨量為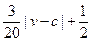 ,
,
故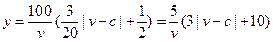 .
.
(II)由(I)知,當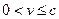 時,
時,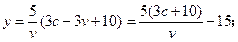
當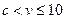 時,
時,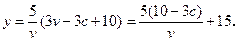
故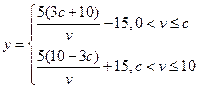 。
。
(1)當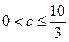 時,
時,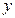 是關于
是關于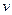 的減函數.故當
的減函數.故當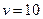 時,
時,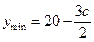 。
。
(2) 當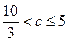 時,在
時,在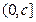 上,
上,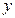 是關于
是關于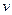 的減函數;在
的減函數;在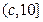 上,
上,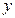 是關于
是關于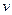 的增函數;故當
的增函數;故當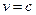 時,
時,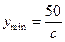 。
。











