19.(本題滿分12分)
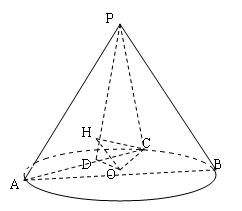
如圖3,在圓錐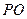 中,已知
中,已知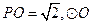 的直徑
的直徑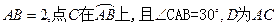 的中點.
的中點.
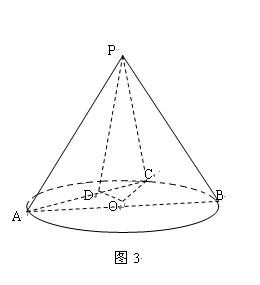
(I)證明:
(II)求直線和平面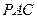 所成角的正弦值.
所成角的正弦值.
(II)由(I)知, 又
又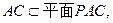 所以平面
所以平面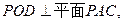 在平面
在平面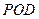 中,過
中,過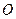 作
作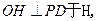 則
則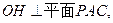 連結
連結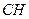 ,則
,則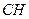 是
是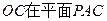 上的射影,所以
上的射影,所以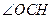 是直線
是直線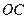 和平面
和平面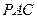 所成的角.
所成的角.
在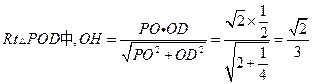
在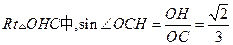
20.(本題滿分13分)
某企業在第1年初購買一臺價值為120萬元的設備M,M的價值在使用過程中逐年減少,從第2年到第6年,每年初M的價值比上年初減少10萬元;從第7年開始,每年初M的價值為上年初的75%.
(I)求第n年初M的價值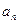 的表達式;
的表達式;
(II)設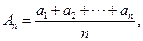 若
若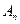 大于80萬元,則M繼續使用,否則須在第n年初對M更新,證明:須在第9年初對M更新.
大于80萬元,則M繼續使用,否則須在第n年初對M更新,證明:須在第9年初對M更新.
解析:(I)當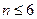 時,數列
時,數列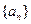 是首項為120,公差為
是首項為120,公差為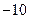 的等差數列.
的等差數列.
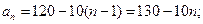
當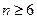 時,數列
時,數列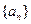 是以
是以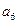 為首項,公比為
為首項,公比為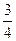 為等比數列,又
為等比數列,又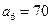 ,所以
,所以
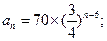
因此,第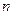 年初,M的價值
年初,M的價值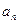 的表達式為
的表達式為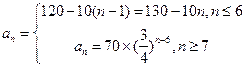
(II)設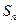 表示數列
表示數列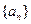 的前
的前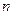 項和,由等差及等比數列的求和公式得
項和,由等差及等比數列的求和公式得
當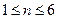 時,
時,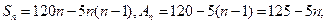
當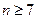 時,
時,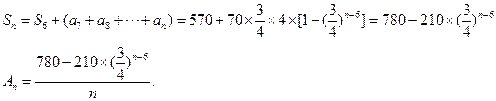
因為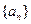 是遞減數列,所以
是遞減數列,所以 是遞減數列,又
是遞減數列,又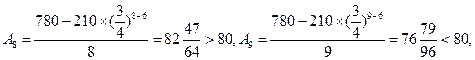
所以須在第9年初對M更新.
21.已知平面內一動點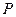 到點F(1,0)的距離與點
到點F(1,0)的距離與點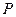 到
到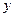 軸的距離的等等于1.
軸的距離的等等于1.
(I)求動點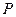 的軌跡
的軌跡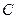 的方程;
的方程;
(II)過點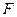 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線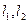 ,設
,設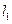 與軌跡
與軌跡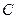 相交于點
相交于點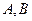 ,
,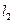 與軌跡
與軌跡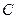 相交于點
相交于點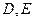 ,求
,求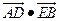 的最小值.
的最小值.
(II)由題意知,直線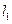 的斜率存在且不為0,設為
的斜率存在且不為0,設為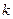 ,則
,則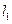 的方程為
的方程為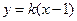 .
.
由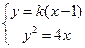 ,得
,得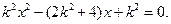
設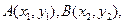 則
則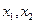 是上述方程的兩個實根,于是
是上述方程的兩個實根,于是
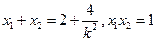 .
.
因為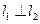 ,所以
,所以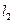 的斜率為
的斜率為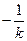 .
.
設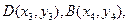 則同理可得
則同理可得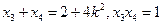
故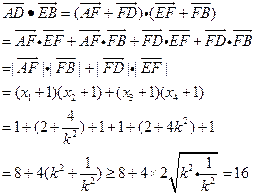
當且僅當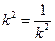 即
即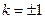 時,
時,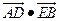 取最小值16.
取最小值16.
22.(本小題13分)
設函數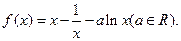
(I)討論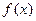 的單調性;
的單調性;
(II)若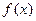 有兩個極值點
有兩個極值點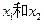 ,記過點
,記過點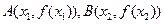 的直線的斜率為
的直線的斜率為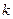 ,問:是否存在
,問:是否存在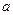 ,使得
,使得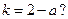 若存在,求出
若存在,求出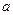 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.











